TOANMATH.com giới thiệu đến đọc giả bài viết hướng dẫn phương pháp chứng minh đường thẳng song song với mặt phẳng, đây là một dạng toán cơ bản thường gặp khi học chủ đề hình học không gian. Bài viết trình bày định nghĩa, các định lý và một số ví dụ minh họa điển hình chứng minh đường thẳng song song với mặt phẳng.
Định nghĩa: Một đường thẳng và một mặt phẳng song song với nhau nếu chúng không có điểm chung.
Các định lí: Định lí 1. Một đường thẳng (không nằm trên $(alpha )$) song song với mặt phẳng $(alpha )$ khi và chỉ khi nó song song với một đường thẳng nằm trên $(alpha )$.
Định lí 2. Nếu đường thẳng $a$ song song với mặt phẳng $(alpha )$ thì bất kì mặt phẳng nào chứa $a$ mà cắt $(alpha )$ theo giao tuyến $b$ thì $b$ song song với $a.$
Định lí 3. Hai mặt phẳng cắt nhau cùng song song với một đường thẳng thì giao tuyến của nó song song với đường thẳng đó.
Ví dụ minh họa: Ví dụ 1: Cho tứ diện $ABCD$ có $G$ là trọng tâm $ΔABD.$ Lấy điểm $M$ trên cạnh $BC$ sao cho $MB = 2MC.$ Chứng minh $MG$ song song mặt phẳng $(ACD).$
Gọi $I$ là trung điểm $AD.$ Do $G$ là trọng tâm $ΔABD$ nên $frac{{BG}}{{GI}} = 2$, mà $frac{{BM}}{{CM}} = 2$ nên $frac{{BG}}{{GI}} = frac{{BM}}{{MC}}.$ Áp dụng định lí Thales trên mặt phẳng $(BIC)$, ta có $GM//IC.$ Mà $IC$ nằm trong mặt phẳng $(ACD).$ Do đó $GM//mp(ACD).$
Ví dụ 2: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành. Gọi $M$, $N$, $P$ lần lượt là trung điểm $AB$, $CD$ và $SA.$ a) Chứng minh $SB$ và $SC$ song song với mặt phẳng $(MNP).$ b) Gọi $G_1$, $G_2$ lần lượt là trọng tâm $ΔABC$ và $ΔSBC.$ Chứng minh ${G_1}{G_2}$ song song mặt phẳng $(SAC).$
a) Ta có $MP//SB$ và $MP$ nằm trong mặt phẳng $(MNP).$ Vậy $SB//mp (MNP).$ Gọi $O$ là tâm hình bình hành $ABCD.$ Ta có $OP//SC$ và $OP$ nằm trong mặt phẳng $(MNP).$ Vậy $SC // mp (MNP).$ b) Gọi $I$ là trung điểm $BC.$ $G_1$ trọng tâm $ΔABC$ $ Rightarrow frac{{I{G_1}}}{{IA}} = frac{1}{3}.$ $G_2$ trọng tâm $ΔSBC$ $ Rightarrow frac{{I{G_2}}}{{IS}} = frac{1}{3}.$ Vây $frac{{I{G_1}}}{{IA}} = frac{{I{G_2}}}{{IS}}$ $ Rightarrow {G_1}{G_2}//SA.$ Mà $SA$ nằm trong mặt phẳng $(SAC)$ nên ${G_1}{G_2}//mp(SAC).$
Ví dụ 3: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thang, đáy lớn $AD$ và $AD = 2BC.$ Gọi $G$ là trọng tâm $ΔSCD$, $O$ là giao điểm $AC$ và $BD.$ a) Chứng minh $OG$ song song mặt phẳng $(SBC).$ b) Gọi $M$ là trung điểm $SD.$ Chứng minh $MC$ song song mặt phẳng $(SAB).$ c) Lấy $I$ trên đoạn $SC$ sao cho $SI = frac{2}{3}SC.$ Chứng minh $SA$ song song mặt phẳng $(BID).$
a) Gọi $H$ là trung điểm $SC.$ Ta có: $frac{{DG}}{{DH}} = frac{2}{3}.$ Do $BC//AD$ $ Rightarrow frac{{OD}}{{OB}} = frac{{AD}}{{BC}} = 2$ $ Rightarrow OD = 2OB$ $ Rightarrow frac{{OD}}{{BD}} = frac{2}{3}.$ Vậy $frac{{DG}}{{DH}} = frac{{OD}}{{BD}} = frac{2}{3}$ $ Rightarrow OG//BH.$ Mà $BH subset mp(SBC)$ $ Rightarrow OG//mp(SBC).$ b) Gọi $N$ là trung điểm $SA.$ Ta có: $overrightarrow {NM} = overrightarrow {BC} = frac{1}{2}overrightarrow {AD}.$ Vậy $NMCB$ là hình bình hành $ Rightarrow CM//BN.$ Mà $BN subset mp(SAB)$ $ Rightarrow CM//mp(SAB).$ c) Ta có: $SI = frac{2}{3}SC$ $ Rightarrow frac{{CI}}{{CS}} = frac{1}{3}.$ $BC//AD$ $ Rightarrow frac{{CO}}{{OA}} = frac{{BC}}{{AD}} = frac{1}{2}$ $ Rightarrow frac{{CO}}{{CA}} = frac{1}{3}.$ Vậy: $frac{{CO}}{{CA}} = frac{{CI}}{{CS}}$ $ Rightarrow OI//SA$ mà $OI subset mp(BID)$ $ Rightarrow SA//mp(BID).$ [ads] Ví dụ 4: Cho hai hình bình hành $ABCD$ và $ABEF$ không cùng nằm trong một mặt phẳng có tâm lần lượt là $O$, $O’.$ a) Chứng minh $OO’$ song song mặt phẳng $(ADF)$ và $(BCE).$ b) Lấy hai điểm $M$, $N$ trên cạnh $AE$ và $BD$ sao cho $AM = frac{1}{3}AE$ và $BN = frac{1}{3}BD$. Chứng minh $MN$ song song mặt phẳng $(CDFE).$
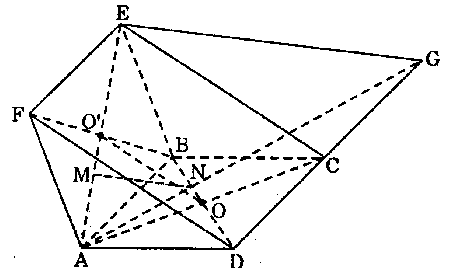
a) Ta có: $OO’$ là đường trung bình của $ΔAEC$ nên $OO’//EC$ mà $EC$ nằm trong mặt phẳng $(BCE)$ nên $OO’//mp(BCE).$ Tương tự: $OO’//DF$ nên $OO’//mp(ADF).$ b) Trong mặt phẳng $(ABCD)$, $AN$ cắt $CD$ tại $G.$ Ta có: $AB//DG$ $ Rightarrow frac{{NB}}{{ND}} = frac{{NA}}{{NG}} = frac{1}{2}.$ Mặc khác: $frac{{AM}}{{ME}} = frac{1}{2}$ (giả thiết). Vậy $frac{{NA}}{{NG}} = frac{{MA}}{{ME}}$ nên $MN//EG.$ Mà $EG$ nằm trong mặt phẳng $(CDFE)$ nên $MN // mp (CDEF).$
Ví dụ 5: Cho hình chóp $S.ABCD$ có $ABCD$ là hình bình hành. Gọi $M$ là trung điểm của $SA.$ a) Tìm giao tuyến của hai mặt phẳng $(SAD)$ và $(SBC).$ b) Tìm giao điểm của $SB$ và mặt phẳng $(MCD).$
a) Hai mặt phẳng $(SAD)$ và $(SBC)$ đã có chung điểm $S.$ Ta có $BC // AD$ mà $AD ∈ mp (SAD)$ $⇒ BC // mp (SAD).$ Mặt phẳng $(SBC)$ chứa $BC.$ Vậy mặt phẳng $(SAD)$ và $(SBC)$ cắt nhau theo giao tuyến $St//AD//BC.$ b) Ta có $AB // CD$ $⇒ AB // mp (MDC).$ Mặt phẳng $(SAB)$ chứa $AB$ sẽ cắt mặt phẳng $(MDC)$ theo giao tuyến $Mx//AB//CD.$ Trong mặt phẳng $(SAB)$ gọi $N$ là giao điểm của $Mx$ và $SB$ thì $N$ là giao điểm của $SB$ và mặt phẳng $(MDC).$
Ví dụ 6: Cho hình chóp $S.ABCD$ có $ABCD$ là hình bình hành. Lấy điểm $M$ trên $SD.$ a) Tìm giao điểm $N$ của $SC$ và $(ABM).$ b) Gọi $K$ là giao điểm của $AM$ và $BN.$ Chứng minh khi $M$ thay đổi trên $SD$ thì $SK$ luôn luôn song song với mặt phẳng cố định.
a) Ta có $CD // AB$ mà $AB ⊂ (ABM)$ $⇒ CD // (ABM).$ Mặt phẳng $(SCD)$ chứa $CD.$ Mặt phẳng $(SCD)$ và mặt phẳng $(MAB)$ có điểm chung là $M.$ Vậy $(SCD) ∩ (MAB) = Mt // AB.$ Trong mặt phẳng $(SCD)$, $Mt ∩ SC$ tại $N$ thì $N = SC ∩ (ABM).$ b) Hiển nhiên $S ∈ (SAD) ∩ (SBC).$ Mặt khác: $K ∈ AM ⇒ K ∈ (SAD).$ $K ∈ BN ⇒ K ∈ (SBC).$ Vậy $SK = (SAD) ∩ (SBC).$ Hai mặt phẳng $(SAD)$ và $(SBC)$ chứa hai đường thẳng $AD // BC$, vậy giao tuyến $SK$ của chúng song song $AD // BC.$ Do $SK // AD$ mà $AD ⊂ (ABCD)$ nên $SK$ song song mặt phẳng cố định $(ABCD).$
Bài tập tự luyện: Bài tập 1: Cho tứ diện $ABCD.$ Mặt phẳng $(P)$ di động luôn song song $AB$ và $CD$ lần lượt cắt $AC$, $AD$, $BC$, $BD$ tại $M$, $N$, $E$, $F.$ a) Chứng minh $MNEF$ là hình bình hành. b) Tìm tập hợp tâm $I$ của $MNEF.$
Bài tập 2: Cho hai hình thang $ABCD$ và $ABEF$ nằm trong hai mặt phẳng phân biệt. Lấy $M$, $N$ lần lượt trên $AB$, $CE$ sao cho $frac{{AM}}{{AB}} = frac{{CN}}{{CE}} = x$ $(0<x<1).$ Chứng minh khi $x$ thay đổi thì $MN$ luôn song song mặt phẳng $(BCE).$
Bài tập 3: Cho tứ diện $ABCD.$ Gọi $I$, $I’$ lần lượt là tâm đường tròn nội tiếp của tam giác $ABC$ và $ABD.$ Chứng minh rằng: a) Điều kiện cần và đủ để $II’$ song song $(BCD)$ là $frac{{BC}}{{BD}} = frac{{AB + AC}}{{AB + AD}}.$ b) Điều kiện cần và đủ để $II’$ song song $(BCD)$ và $(ACD)$ là $BC = BD$ và $AC = AD.$
Bài tập 4: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành. Lấy $M$ là điểm di động trên $AB.$ Mặt phẳng $(α)$ qua $M$ song song với $SA$ và $BC$ cắt $SB$, $SC$, $SD$ tại $N$, $P$, $Q.$ a) Chứng minh $MNPQ$ là hình thang. b) Gọi $I$ là giao điểm của $MN$ và $PQ.$ Chứng minh $I$ di động trên một đường cố định.
Bài tập 5: Cho tứ diện $ABCD.$ Gọi $(α)$ là mặt phẳng di động luôn song song với $AB$ và $CD$ cắt $AC$, $AD$, $BC$, $BD$ tại $M$, $N$, $E$, $F.$ a) Chứng minh $MNEF$ là hình bình hành. b) Tìm tập hợp các tâm $I$ của $MNEF.$
Bài tập 6: Cho tứ diện $ABCD.$ Lấy $E$, $F$, $G$, $H$ lần lượt trên $AD$, $AB$, $BC$, $CD$ sao cho $frac{{EA}}{{ED}} = frac{{FA}}{{FB}} = frac{{GC}}{{GB}} = frac{{HC}}{{HD}}.$ a) Chứng minh $EFGH$ là hình bình hành. b) Chứng minh $AC$ song song với $(EFGH)$ và $BD$ song song với $(EFGH).$
Bài tập 7: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành. Gọi $M$ là điểm di động trên $SC.$ Mặt phẳng $(P)$ chứa $AM$ và song song với $BD.$ a) Tìm giao điểm $E$, $F$ của $SB$, $SD$ với $(P).$ b) Gọi $I$, $J$ lần lượt là giao điểm của $ME$ với $CB$, $MF$ với $CD.$ Chứng minh $I$, $J$, $A$ thẳng hàng.
Bài tập 8: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thang với $AB$ là đáy lớn. Gọi $M$, $N$ lần lượt là trung điểm của $SA$, $SB.$ a) Chứng minh $MN$ song song với $CD.$ b) Tìm điểm $P$ là giao điểm của $SC$ và $(ADN).$ c) Gọi $I$ là giao điểm của $AN$ với $DP.$ Chứng minh $SI//AB//CD.$ d) Tứ giác $SABI$ là hình gì?

