1. Tổng hợp kiến thức ôn thi giữa kì 2 môn toán 10
1.1 Hàm số
– Khái niệm: Với mỗi giá trị của 
có một và chỉ một giá trị y tương ứng với thì ta có một hàm số. Trong đó:
- x là biến số
- y là là hàm số của x
- D là tập xác định của hàm số
+ Tất cả các giá trị y nhận được gọi là tập giá trị của hàm số.
– Đồ thị hàm số: Đồ thị hàm số y = f(x) xác định trên tập D là tập hợp tất cả các điểm M(x) ; f(x) trên mặt phẳng tọa độ với mọi .
– Hàm số y = f(x) đồng biến trên khoảng (a;b) nếu:
– Hàm số y = f(x) nghịch biến trên khoảng (a;b) nếu:
1.2 Hàm số bậc hai
– Hàm số bậc hai là hàm số được cho bởi công thức: y = ax2 + bx + c, trong đó:
- x là biến số
- a, b, c là các hằng số (a
0) - TXĐ:
– Đồ thị hàm số bậc 2: y = ax2 + bx + c (a 0) là đường parabok có đỉnh là điểm I , có trục đối xướng là đường thẳng . Đồ thị hàm số có bề lõm quay lên trên nếu a > 0, quay xuống dưới nếu a < 0.
– Cách vẽ đồ thị y = ax2 + bx + c:
- Bước 1: Xác định tọa độ đỉnh I ;
- Bước 2: Vẽ trục đối xứng ;
- Bước 3: Xác định tọa độ giao điểm của đồ thị với trục tung, trục hoành (nếu có) và một vài điểm đặc biệt trên đồ thị;
- Bước 4: Vẽ đồ thị bằng cách nối các điểm với nhau.
1.3 Dấu của tam thức bậc hai
– Tam thức bậc hai với x là biểu thức có dạng ax2 + bx + c , trong đó:
- a, b,c là số thực cho trước (a 0)
- a,b,c là hệ số của tam thức bậc 2
– Cho tam thức bậc 2 f(x) = ax2 + bx + c (a 0)
+ Nếu < 0 thì f(x) cùng dấu với hệ số a
+ Nếu = 0 thì f(x) cùng dấu với hệ số a -b/2a và f(-b/2a) = 0.
+ Nếu > 0 thì tam thức f(x) có 2 nghiệm phân biệt . Khi đó f(x) cùng dấu với a ; f(x) trái dấu với hệ số a .
Khóa học DUO cung cấp cho các em nền tảng kiến thức toán vững chắc, bứt phá điểm 9+ trong mọi bài kiểm tra trên lớp.
1.4 Phương trình quy về phương trình bậc hai
a. Phương trình dạng
– Để giải phương trình dạng ta thực hiện các bước sau:
Bước 1: Bình phương 2 vế và giải phương trình nhận được.
Bước 2: Thử lại giá trị x tìm được ở trên có thỏa mãn phương trình không và kết luận nghiệm.
b. Phương trình dạng
– Để giải phương trình dạng , ta thực hiện theo 2 bước như sau:
Bước 1: Bình phương hai vế và giải phương trình nhận được
Bước 2: Thử lại giá trị x tìm được ở trên có thỏa mãn phương trình đã cho hay không và kết luận nghiệm.
1.5 Phương trình đường thẳng
a. Phương trình tổng quát của đường thẳng
– Véc tơ được gọi là véc tơ pháp tuyến của đường thẳng nếu giá trị của nó vuông góc với
+ Nếu là véc tơ pháp tuyến của đường thẳng thì k (k 0) cũng là véc tơ pháp tuyến của .
+ Có thể xác định được một đường thẳng nếu biết 1 điểm và một véc tơ pháp tuyến của nó.
– Trong mặt phẳng tọa độ, mọi đường thẳng đều có phương trình tổng quát ax + by + c = 0 với a,c,c không đồng thời bằng 0. Ngược lại mỗi phương trình dạng ax + by + c = 0 với a,c,c không đồng thời bằng 0 đều là phương trình của một đường thẳng nhận (a;b) là véc tơ pháp tuyến.
b. Phương trình tham số của đường thẳng
Véc tơ được gọi là véc tơ chỉ phương của đường thẳng nếu giá của nó song song hoặc trùng với .
+ Nếu là véc tơ chỉ phương của đường thẳng thì k (k 0) cũng là véc tơ chỉ phương của đường thẳng .
+ Đường thẳng hoàn toàn xác định nếu biết một điểm và một véc tơ chỉ phương của nó.
+ Hai véc tơ và vuông góc với nhau, vì vậy nếu là véc tơ pháp tuyến của đường thẳng thì là véc tơ chỉ phương của đường thẳng đó và ngược lại.
– Cho đường thẳng đi qua điểm A (xo; yo) và có véc tơ chỉ phương (a;b). Khi đó điểm M(x;y) thuộc đường thẳng khi và chỉ khi tồn tại một số thực t sao cho hay:
Hệ (1) được gọi là phương trình tham số của đường thẳng (t là tham số).
1.6 Vị trí tương đối giữa hai đường thẳng, góc và khoảng cách
a. Vị trí tương đối giữa hai đường thẳng:
– Trên mặt phẳng tọa độ, xét hai đường thẳng
Khi đó, tọa độ giao điểm của là nghiệm của hệ phương trình:
Ta có:
- cắt tại M(xo; yo) hệ (2) có nghiệm duy nhất (xo; yo).
- // hệ (2) vô nghiệm.
- trùng hệ (2) có vô số nghiệm).
– Lưu ý:
+ Dựa vào véc tơ chỉ phương hoặc véc tơ pháp tuyến của , ta có:
- // hoặc trùng nhau cùng phương cùng phương.
- cắt không cùng phương không cùng phương.
b. Góc giữa hai đường thẳng
– Hai đường thẳng cắt nhau tạo thành bốn góc, số đo của góc không tù được gọi là số đo góc giữa hai đường thẳng. Góc giữa hai đường thẳng song song hoặc trùng nhau được quy ước bằng 0o.
– Cho hai đường thẳng: và với các véc tơ pháp tuyến và tương ứng. Khi đó góc giữa hai đường thẳng đó là được xác định:
– Chú ý:
– Nếu có các véc tơ chỉ phương thì góc giữa cũng được xác định thông qua công thức:
c. Khoảng cách từ một điểm đến một đường thẳng
– Cho điểm M(xo;yo) và đường thẳng = ax + by + c = 0. Khoảng cách từ điểm M đến đường thẳng được kí hiệu là d(M,) có công thức tính như sau:
Đừng bỏ qua bộ sách toán – lý – hóa được biên soạn bởi các thầy cô giáo trường chuyên chỉ có duy nhất tại VUIHOC thôi bạn nhé!
1.7 Đường tròn
a. Phương trình đường tròn
– Điểm M đường tròn (C) có tâm I (a;b) và bán kính R có phương trình đường tròn là:
(x – a)2 + (y – b)2 = R2
– Phương trình x2 + y2 – 2ax – 2by + c = 0 là phương trình của đường tròn (C) a2 + b2 -c > 0. Khi đó, (C) có tâm I (a,b) và bán kính
b. Phương trình tiếp tuyến của đường tròn:
– Cho điểm M (xo,yo) đường tròn (C): (x – a)2 + (y – b)2 = R2. Khi đó tiếp tuyến của (C) tại M (xo;yo) có véc tơ pháp tuyến =(a – xo;b-yo) và phương trình:
(a – xo).(x – xo) + ( b – yo).(y – yo) = 0.
1.8 Ba đường conic
a. Elip
– Cho hai điểm cố định và phân biệt F1; F2. Đặt F1F2 = 2c > 0. Cho số thực a > c. Tập hợp các điểm M sao cho MF1 + MF2 = 2a được gọi là đường elip. F1 F2 được gọi là tiêu điểm, F1F2 = 2c được gọi là tiêu cự của elip đó.
– Phương trình chính tắc của elip:
b. Hypebol
– Cho hai điểm cố định và phân biệt F1; F2. Đặt F1F2 = 2c. Cho số thực dương a < c. Tập hợp các điểm M sao cho |MF1 – MF2| = 2a được gọi là đường hypebol. F1 F2 được gọi là tiêu điểm, F1F2 = 2c được gọi là tiêu cự của hypebol đó.
– Phương trình chính tắc của hypebol:
c. Parabol
– Cho một điểm F cố định và một đường thẳng cố định không đi qua F. Tập hợp các điểm M cách đều F và được gọi là đường parabol. Điểm F được gọi là tiêu điểm, được gọi là đường chuẩn. Khoảng cash từ F đến được gọi là tham số tiêu của parabol đó.
– Phương trình chính tắc của parabol: y2 = 2px (p > 0).
2. Ôn thi giữa kì 2 môn Toán 10: Các dạng bài tập và cách giải
2.1 Các dạng bài về hàm số
a. Tính giá trị của hàm số tại một điểm.
Cách làm: Tính giá trị của hàm số f(x), tại x = a, ta thay a vào biểu thức hàm số được f(a). Tính giá trị.
b.Tìm tập xác định của hàm số.
Cách làm: TXĐ của hàm số y = f(x) là tập hợp các giá trị của x sao cho biểu thức f(x) đó có nghĩa.
có nghĩa khi f(x) 0.
có nghĩa khi f(x) 0.
có nghĩa khi f(x) > 0.
có nghĩa khi g(x) 0.
c. Xác định tính chẵn, lẻ của hàm số.
– Xét tập D là tập đối xứng, tính f(-x)
- Nếu f(-x) = f(x) => Hàm số chẵn, đồ thị nhận trục tung làm trục đối xứng.
- Nếu f(-x) = -f(x) => Hàm số lẻ, đồ thị nhận trục hoành làm trục đối xứng.
d. Bài tập liên quan tính đồng biến, nghịch hàm số bậc nhất.
– Khi a > 0: Hàm số đồng biến trên R.
– Khi a < 0: Hàm số nghịch biến trên R
2.2 Các dạng bài về hàm số bậc 2
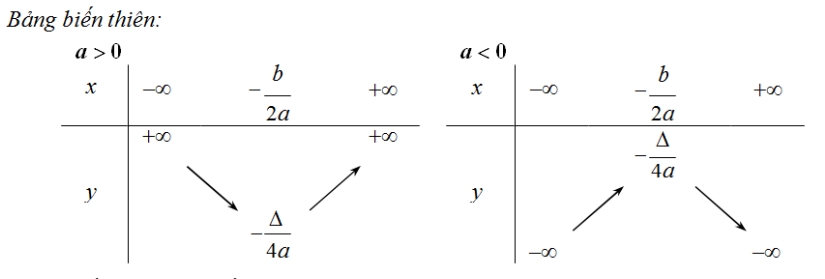
a. Lập bảng biến thiên và vẽ đồ thị hàm số
– Các bước vẽ đồ thị (P): y = ax2 + bx + c (a 0)
- TXĐ: D = R
- Xác định đỉnh:
- Xác định trục đối xứng:
- Xác định bề lõm và bảng biến thiên: Hướng lên trên nếu a > 0 ; hướng xuống dưới nếu a < 0
- Tìm các giao điểm đặc biệt với trục tung và trục hoành
- Vẽ đồ thị.
b. Xác định các hệ số a,b,c khi biết tính chất của đồ thị hoặc hàm số
– Lập hệ phương trình với các ẩn a,b,c biểu thị tính chất của đồ thị hoặc hàm số. Giải hệ PT tìm a,b,c.
– Lưu ý:
- Đỉnh I của (P) luôn thuộc (P) =>
- P có đỉnh là I
c. Tìm tọa độ giao điểm của hai đồ thị
– Xét phương trình hoành độ giao điểm f(x) = g(x) (1)
- Nếu (1) có n nghiệm thì hai đồ thị có n điểm chung.
- Tìm tung độ giao điểm ta thay nghiệm x vào y = f(x) hoặc y = g(x) để tính y.
Khóa học DUO cung cấp cho các em nền tảng kiến thức toán vững chắc, bứt phá điểm 9+ trong mọi bài kiểm tra trên lớp.
2.3 Các dạng bài về đường thẳng
a. Vị trí tương đối giữa hai đường thẳng:
Cho d: y = ax + b và d: y = a’x + b’ ( với a, a’ 0)
- d d’ a = a’ và b = b’
- d // d’ a = a’ và b b’
- d cắt d’ a a’
- d d’ a.a’ = 1
- d cắt d’ tại một điểm trên trục tung a a’ và b = b’
b. Lập phương trình đường thẳng Dạng 1: Viết phương trình đường thẳng qua 2 điểm A, B. Nếu xA xB:
- PT đường thẳng d có dạng y = ax + b (1)
- Thế tọa độ A và B vào (1) ta được hệ PT 2 ẩn a và b.
- Giải hệ PT tính được a và b.
Dạng 2: Viết PT đường thẳng qua A và song song với y = ax’ + b’
- PT đường thẳng d: y = ax + b (1)
- A d => thay tọa độ điểm A vào (1) ta có phương trình (*)
- Vì d // => a = a’ (**)
- Giải hệ phương trình (*) và (**) ta tìm được a và b.
Dạng 3: Viết PT đường thẳng qua điểm A và vuông góc với y = ax’ + b’
- PT đường thẳng d: y = ax + b (1)
- A d => thay tọa độ điểm A vào (1) ta có phương trình (*)
- d => a.a’ = 1 (**)
- Giải hệ phương trình (*) và (**) ta tìm được a và b.
2.4 Các dạng bài tập về đường tròn
a. Tìm tâm và bán kính của đường tròn
Cách 1: Dựa vào phương trình đường tròn đề bài cho:
- PT: (x-a)2 + (y-b)2 = R2 ta có tâm I (a,b) ; bán kính R
- PT: x2 + y2 – 2ax – 2by + c = 0 có tâm I (a;b); bán kính
Cách 2: Biến đổi PT x2 + y2 – 2ax – 2by + c = 0 về phương trình (x-a)2 + (y-b)2 = R2 để tìm tâm I (a; b), bán kính R.
b. Viết phương trình đường tròn
Cách 1: Tìm tọa độ tâm I (a;b) của đường tròn (C), tìm bán kính R của đường tròn (C), viết PT đường tròn.
Cách 2: Giả sử PT có dạng x2 + y2 – 2ax – 2by + c = 0, ta thiết lập PT 3 ẩn a,b,c, sau đó giải hệ và thay vào PT đường tròn.
c. Vị trí tương đối của 2 đường tròn, đường tròn với đường thẳng:
– Cho 2 đường tròn (C1) có tâm I1, bán kính R1 và tròn (C2) có tâm I2, bán kính R2:
- Nếu I1I2 > R1 + R2 => Hai đường tròn không có điểm chung.
- Nếu I1I2 = R1 + R2 => Hai đường tròn tiếp xúc nhau.
- Nếu I1I2 = |R1 – R2| thì hai đường tròn tiếp xúc trong.
- Nếu R1 – R2 < I1I2 < R1 + R2 thì hai đường tròn cắt nhau tại hai điểm (với R1 > R2 ).
– Cho đường tròn (C0 có tâm I(xo;yo), bán kính R và đường thẳng : y = ax + by + c = 0.
+ Tính khoảng cách từ d(I;):
+ Tính bán kính R của (C)
+ So sánh d(I;) với R:
- Nếu d(I;) = R => tiếp xúc với (C)
- Nếu d(I;) > R => không giao với (C)
- Nếu d(I;) < R => giao với (C) tại 2 điểm phân biệt.
Sổ tay hack điểm thi toán, tổng hợp các công thức, tips học toán được tiết lộ bởi các thầy cô trường chuyên. Đăng ký ngay để nhận ưu đãi 50% từ VUIHOC nhé!
3. Luyện tập giải các dạng bài khó ôn thi giữa kì 2 toán 10
Bài 1: Tìm các giá trị của m để phương trình có 2 nghiệm phân biệt
Lời giải:
Xét f(x) = x2 – x + 1. Ta có bảng biến thiên sau:
Vậy phương trình có 2 nghiệm phân biệt
Bài 2: a. Tìm phương trình (P): ax2 + bx + c , biết rằng ( P) đi qua ba điểm A, B, C như hình vẽ.
b. Giải phương trình trên tập số thực
Lời giải:
a. Dựa vào đồ thị ta có (P) đi qua ba điểm A(1;-1) ; B(2;3) ; C(-1;-3)
Ta có:
Vậy (P) có phương trình là y = x2 + x – 3
b. Ta có:
hoặc
Vậy tập nghiệm của PT: S = {0}
Bài 3: Cho ABC có trọng tâm G. gọi N, P lần lượt là các điểm thỏa mãn và . Tìm k để G, P, N thẳng hàng.
Lời giải
Gọi M là trung điểm của đoạn thẳng BC.
Đặt ( vì k = 1 không thỏa mãn)
Ta có:
Mà 3 điểm G, P, N thẳng hàng => cùng phương
Bài 4: Để xác định định chiều cao của một thang trượt tuyết được xác định từ P đến Q (như hình vẽ). Một nhà khảo sát đo lường đã ước tính góc DPQ = 25o, sau đó nhà khảo sát đi bộ ra xa cách vị trí P 1000ft và tiến hành đo được góc QRD = 15o. Tính khoảng cách từ P đến Q theo đơn vị m. Biết rằng 1ft = 0,3048m, làm tròn đến chữ số hàng đơn vị.
Lời giải:
Gọi chiều cap QD là x ( x > 0)
Do QPD vuông tại D, áp dụng tỉ số lượng giác ta có DP = x. cot25o
Theo đề bài ta có: DR – DP = 1000 x.cot15o – x.cot25o = 1000
Khi đó ta có:
Trên đây là toàn bộ kiến thức trọng tâm ôn thi giữa kì 2 môn toán 10 mà VUIHOC đã tổng hợp dựa trên các bài học trong chương trình toán 10 mới. Để làm tốt bài thi giữa kỳ 2 môn Toán, bên cạnh việc ôn tập lý thuyết, các em cần thực hành làm nhiều bài tập với các dạng bài khác nhau để nắm chắc cách giải các dạng bài đó. Chúc các em làm bài thi tốt và đạt được điểm số như mong muốn.
>> Mời bạn tham khảo thêm:
- Đề thi giữa kì 2 môn Toán 10
- Ôn thi giữa kì 2 môn Lý 10
- Ôn thi giữa kì 2 môn Hóa 10
- Ôn thi giữa kì 2 môn Tiếng Anh 10
- Ôn thi giữa kì 2 môn Ngữ Văn 10
