MATHX gửi đến quý phụ huynh và các em học sinh đề kiểm tra giữa học kì 1 trường THCS Xuân La – Tây Hồ năm học 2025 – 2026 kèm đáp án tham khảo.

Bài 3. (2 điểm)
Hướng dẫn
a) ( 2x^2 – 8xy )
= ( 2x(x – 4y) )
b) ( y^2(x – 1) + 4(1 – x) )
= ( y^2(x – 1) – 4(x – 1) )
= ( (x – 1)(y^2 – 4) )
= ( (x – 1)(y^2 – 2^2) )
= ( (x – 1)(y – 2)(y + 2) )
c) ( x^2 – 2xy + y^2 – xz + yz )
= ( (x^2 – 2xy + y^2) – (xz – yz) )
= ( (x – y)^2 – z(x – y) )
= ( (x – y)(x – y – z) )
Bài 4. (1 điểm)
Hướng dẫn
a) Biểu thức đại số tính quãng đường Quảng Ninh – Hà Nội theo ( x ) là:
( (9x + 20)(x – 2) , (text{km}) )
b) Với ( x = 5 ), quãng đường Quảng Ninh – Hà Nội là:
( (9 cdot 5 + 20) cdot (5 – 2) = 65 cdot 3 = 195 , (text{km}) )
Bài 5. (3,5 điểm)
Hướng dẫn
5.1.
a) Diện tích bề mặt cần sơn là: ( dfrac{1}{2} cdot (20 cdot 4) cdot 21 = 840 , (text{cm}^2) )
b) Thể tích của chậu trồng cây đó là: ( dfrac{1}{3} cdot (20 cdot 20) cdot 35 = dfrac{14000}{3} approx 4666{,}67 , (text{cm}^3) )
5.2.
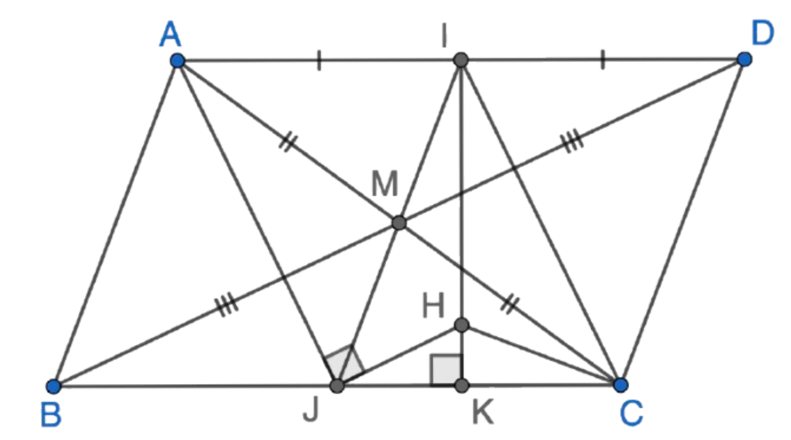
a) Xét tứ giác (ABCD) có hai đường chéo (AC) và (BD) cắt nhau tại (O) thỏa mãn: (O) là trung điểm của (AC) và (BD).
Theo dấu hiệu nhận biết, tứ giác (ABCD) là hình bình hành.
b) Vì tứ giác (ABCD) là hình bình hành (theo phần a)) nên ta có (AD parallel BC).
Do đó (widehat{DAC} = widehat{ACB}) (hai góc so le trong).
Xét (triangle AIM) và (triangle CJM) ta có:
(widehat{IAM} = widehat{MCJ}) (chứng minh trên) (AM = MC) (giả thiết) (widehat{AMI} = widehat{CMJ}) (hai góc đối đỉnh)
Do đó (triangle AIM = triangle CJM) (g.c.g)
Suy ra (AI = CJ) (hai cạnh tương ứng)
Xét tứ giác (AICJ) có cặp cạnh đối (AI) và (CJ) thỏa mãn: (AI parallel CJ) và (AI = CJ).
Theo dấu hiệu nhận biết, tứ giác (AICJ) là hình bình hành.
Do đó ta có (AJ parallel CI).
c) Theo phần b) ta có (AJ parallel CI) mà (HJ perp AJ) nên (HJ perp CI).
Xét (triangle CIJ) ta có:
(IK perp JC) nên (IK) là đường cao của (triangle CIJ). (HJ perp CI) nên (HJ) là đường cao của (triangle CIJ). Mà (IK) cắt (HJ) tại (H) nên (H) là trực tâm của (triangle CIJ).
Do đó, (IH) là đường cao của (triangle CIJ) hay (IH perp CJ). (đpcm)
Bài 6. (0,5 điểm)
Hướng dẫn
Ta có: ( A = 2x^2 + 4y^2 + 6x – 4y – 4xy + 2030 )
= ((4y^2) – (4y + 4xy) + (x^2 + 2x + 1) + (x^2 + 4x + 4) + 2025) = ((2y)^2 – 2 cdot 2y(x+1) + (x+1)^2 + (x+2)^2 + 2025) = ((2y – x – 1)^2 + (x+2)^2 + 2025)
Ta thấy ((2y – x – 1)^2 ge 0) với mọi x, y và ((x+2)^2 ge 0) với mọi x. Suy ra (A ge 0 + 0 + 2025 = 2025).
Dấu “=” xảy ra khi và chỉ khi (begin{cases} (2y – x – 1)^2 = 0 (x+2)^2 = 0 end{cases})
(begin{cases} 2y – x – 1 = 0 x + 2 = 0 end{cases}) (begin{cases} y = dfrac{x+1}{2} x = -2 end{cases}) (begin{cases} y = -dfrac{1}{2} x = -2 end{cases})
Vậy giá trị nhỏ nhất của biểu thức (A) là (2025) khi (x = -2) và (y = -dfrac{1}{2}).
Phụ huynh và học sinh có thể xem file lời giải tại đây:







