Kiến thức về hàm số đơn điệu đã được đề cập tại các lớp học trước, tuy nhiên ở chương trình Toán 12, kiến thức này sẽ xuất hiện những dạng toán phức tạp hơn, đòi hỏi học sinh có kiến thức chắc hơn về hàm số. Kiến thức này cũng thường xuyên xuất hiện trong quá trình ôn thi toán tốt nghiệp THPT QG những năm gần đây, vậy nên hiểu rõ dạng bài này này là rất quan trọng để dễ dàng “ăn điểm” trong kỳ thi. Cùng VUIHOC tìm hiểu để dễ dàng giải các dạng bài tập về xét tính đơn điệu của hàm số nhé!
1. Lý thuyết tính đơn điệu của hàm số
1.1. Định nghĩa tính đơn điệu của hàm số
Cho hàm số y= f(x) xác định trên K (với K là một khoảng hoặc một đoạn hoặc nửa khoảng).
-
Hàm số y=f(x) là đồng biến (tăng) trên K nếu
 .
. -
Hàm số y=f(x) là nghịch biến (giảm) trên K nếu $forall X_{1}, X_{2} in K, X_{1} < X_{2} Rightarrow f(X_{1}) > f(X_{2})$
Hàm số đồng biến hoặc nghịch biến trên K được gọi chung là đơn điệu trên K.
1.2. Các điều kiện cần và đủ để hàm số đơn điệu
a) Điều kiện cần để hàm số đơn điệu:
Giả sử hàm số y=f(x) có đạo hàm trên khoảng K.
-
Nếu hàm số đồng biến trên khoảng K thì f'(x)=0, K và f'(x)=0 xảy ra tại một số hữu hạn điểm.
-
Nếu hàm số nghịch biến trên khoảng K thì f'(x) 0, K và f'(x)=0 xảy ra tại một số hữu hạn điểm.
b) Điều kiện đủ để hàm số đơn điệu:
Giả sử hàm số y=f(x) có đạo hàm trên khoảng K.
-
Nếu f'(x) >0, K thì hàm số đồng biến trên khoảng K
-
Nếu f'(x) <0, K thì hàm số nghịch biến trên khoảng K
-
Nếu f'(x)=0, K thì hàm số không đổi trên khoảng K
2. Quy tắc xét tính đơn điệu của hàm số
2.1. Tìm tập xác định
Để tìm tập xác định của hàm số y=f(x) là tập giá trị của x để biểu thức f(x) có nghĩa ta có:
Nếu P(x) là đa thức thì:
 có nghĩa
có nghĩa
có nghĩa P(x) > 0
có nghĩa
2.2. Tính đạo hàm
Bảng công thức tính đạo hàm của hàm số cơ bản:
2.3. Lập bảng biến thiên
Giả sử ta có hàm số y = f(x) thì:
-
f’(x) < 0 ở đâu thì hàm số sẽ nghịch biến ở đấy.
-
f’(x) > 0 ở đâu thì hàm số sẽ đồng biến ở đấy.
Quy tắc chúng sẽ là:
-
Ta tính f’(x), sau đó giải phương trình f’(x) = 0 tìm nghiệm.
-
Lập bảng xét dấu f’(x).
-
Sau đó dựa vào bảng xét dấu và kết luận
2.4. Kết luận khoảng đồng biến, nghịch biến của hàm số
Đây là bước quan trọng, ở bước này các em sẽ kết luận được sự đồng biến nghịch biến của hàm số trên khoảng nào. Để hiểu rõ hơn thì cùng tham khảo những ví dụ dưới đây nhé!
Ví dụ: Xét sự đồng biến, nghịch biến của các hàm số:
Giải:
TXĐ: D= R, , y’= 0
x= 2 hoặc x= 4
Ta có bảng biến thiên:
Kết luận hàm số đồng biến trên khoảng $(-infty ; 2)$ và $(4;+infty )$, nghịch biến trên khoảng (2;4)
3. Giải các dạng bài tập về tính đơn điệu của hàm số
3.1. Xét tính đơn điệu của hàm số chứa tham số m
* Hàm số đồng biến, nghịch biến trên TẬP XÁC ĐỊNH
Phương pháp:
-
Đối với hàm đa thức bậc ba: .
Tính , khi đó
-
Hàm đa thức bậc ba y=f(x) đồng biến trên R và
-
Hàm đa thức bậc ba y=f(x) nghịch biến trên R và
-
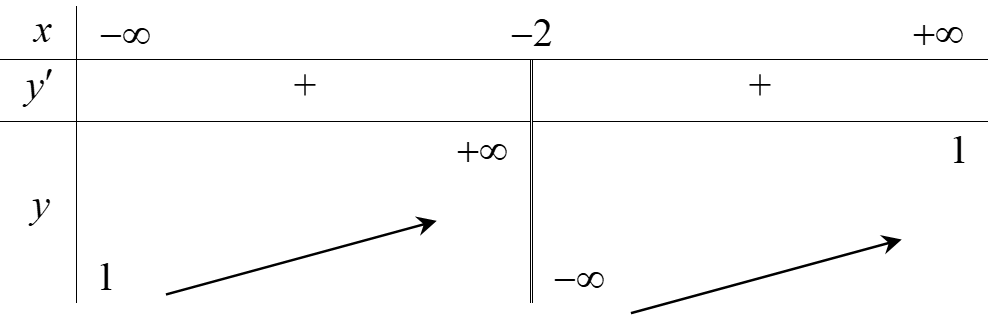
Đối với hàm phân thức bậc nhất:
Tính khi đó:
-
Hàm số đồng biến trên các khoảng xác định khi y’>0 hay (ad-bc)>0
-
Hàm số nghịch biến trên các khoảng xác định khi y’<0 hay (ad-bc)<0
Ví dụ: Cho hàm số: . Xác định m để hàm số đồng biến trên tập xác định.
Lời giải:
-
TXĐ: D = R
-
Tính
Đặt có a = 3; b = -6m; c= 3(2m-1);
Để hàm số đồng biến trên TXĐ khi và chỉ khi:
và
và
Kết luận: Vậy với m = 1 thì hàm số đồng biến trên tập xác định D = R
* Hàm số đồng biến, nghịch biến trên KHOẢNG CHO TRƯỚC
Phương pháp:
-
Bước 1: Kiểm tra tập xác định: Vì bài toán có tham số nên ta cần tìm điều kiện của tham số để hàm số xác định trên khoảng (a;b).
-
Bước 2: Tính f'(x) và tìm điều kiện của tham số để hoặc trên khoảng (a;b) theo yêu cầu bài toán.
Ví dụ: Cho hàm số (*)
Tìm m để hàm số đồng biến trên .
-
Để hàm số đồng biến trên thì .
$large Rightarrow 3x^{2} – 6x – 3 geq 3m$
-
Đặt
-
Cho . Ta có bảng biến thiên sau:
Từ bảng biến thiên ta có
Min
3.2. Tính đơn điệu của hàm số chứa dấu giá trị tuyệt đối
Tìm khoảng đồng biến, nghịch biến của hàm số y=|f(x)|
-
f(x) cụ thể cho trước. VD:
-
f(x) có tham số dạng tách rời. VD:
Bước 1: Khảo sát và lập bảng biến thiên của f(x)
Bước 2: Dùng phép suy bảng biến thiên của hàm số |f(x)|
-
Giữ nguyên phần nằm trên y = 0
-
Lấy đối xứng qua y = 0 phần bên dưới
-
Nhìn vào bảng biến thiên của |f(x)| suy ra đồng biến, nghịch biến
Ví dụ:
Tập hợp tất cả các giá trị của tham số m để hàm số
Giải:
Xét hàm số:
Ta có , f’(x) = 0 x= 0 hoặc x=2
Bảng biến thiên của hàm số f(x)
Vì đồ thị hàm số y=f(x) có được nhờ giữ nguyên phần đồ thị hàm số của y= f(x) ở trục hoành, sau đó lấy đối xứng phần đồ thị ở dưới lên trên qua trục Ox
Nên hàm số y=f(x) đồng biến trên
Đăng ký ngay để sở hữu bí kíp nắm trọn kiến thức và phương pháp giải mọi dạng bài đạt 9+ thi Toán THPT Quốc Gia
3.3. Xét tính đơn điệu của hàm số trên 1 khoảng
Tìm m để hàm số đồng biến trên [-1;3].
-
Để hàm số nghịch biến trên [-1;3] thì f’(x)
-
.
.
-
Đặt
-
Cho . Ta có bảng biến thiên sau:
Từ bảng biến thiên ta có:
⇒
Kết luận: Vậy với thì hàm số sẽ đồng biến trên khoảng [-1;3]
Bài tập tính đơn điệu của hàm số
Câu số 1: Hàm số y = -x3 + 3×2 – 1 đồng biến trên khoảng nào?
A.
B. (0; 2)
C.
D. R
Câu số 2: Các khoảng đồng biến của hàm số y = 2×3 – 6 là
A.
B. (-1; 1)
C. [-1; 1)
D. (0; 1)
Câu số 3: Các khoảng nghịch biến của hàm số y = x3 – 3x -1 là:
A.
B.
C. (-1; 1)
D. (0; 1)
Câu số 4: Các khoảng nghịch biến của hàm số y = 2×3 – 6x + 20 là
A.
B. (-1; 1)
C. [-1; 1]
D. (0; 1)
Câu số 5: Các khoảng đồng biến của hàm số y = -x3 + 3×2 + 1
A.
B. (0; 2)
C. [0; 2]
D. R
Câu số 6: Các khoảng đồng biến của hàm số có dạng y = x3 – 5×2 + 7x – 3 là:
A.
B.
C. [-5; 7]
D. (7; 3)
Câu số 7: Các khoảng nghịch biến của hàm số y = x3 – 6×2 + 9x là:
A.
B. (1; 3)
C.
D.
Câu số 8: Các khoảng nghịch biến của hàm số y = x3 – x2 + 2 là:
A.
B.
C.
D.
Câu số 9: Các khoảng đồng biến của hàm số y = 3x – 4×3
A.
B.
C.
D.
Câu số 10: Các khoảng nghịch biến của hàm số y = 3x – 4×3
A.
B.
C.
D.
Câu số 11: Các khoản đồng biến của hàm số y = x3 -12x + 12 là
A.
B. (-2; 2)
C.
D.
Câu số 12: Hàm số y = -x3 + 3×2 + 9x nghịch biến trên khoảng nào
A. R
B.
C.
D. (-1; 3)
Câu số 13: Hàm số đồng biến trên
A. và
B. và
C. và
D.
Câu số 14: Khoảng nghịch biến của hàm số là
A. R
B.
C. và
D. và
Câu số 15: Mệnh đề nào trong các mệnh đề dưới đây là đúng. Hàm số có dạng
A. Hàm số đồng biến trên (-2; 3)
B. Hàm số nghịch biến trên khoảng (-2; 3)
C. Hàm số đồng biến trên khoảng
D. Hàm số nghịch biến trên khoảng
>> Tham khảo thêm:
- Cách xét tính đơn điệu của hàm số chứa căn và bài tập
- Cách xét tính đơn điệu của hàm số lượng giác và bài tập trắc nghiệm
Trên đây là toàn bộ lý thuyết và cách xét tính đơn điệu của hàm số thường gặp. Tuy nhiên nếu em muốn đạt kết quả thì hãy làm thêm nhiều dạng bài khác nữa. Em có thể truy cập Vuihoc.vn và đăng ký tài khoản để luyện đề! Chúc các em đạt kết quả cao trong kỳ thi THPT Quốc Gia sắp tới.
>> Xem thêm:
- Tổng ôn tập hàm số mũ từ A đến Z
- Tổng ôn tập hàm số lũy thừa, hàm số mũ và hàm số mũ logarit
- Hàm số mũ và logarit – Đầy đủ lý thuyết và bài tập

