Khảo sát và vẽ đồ thị hàm nhất biến. Khảo sát và vẽ đồ thị hàm bậc nhất trên bậc nhất.
Hàm nhất biến. Có dạng $y = frac{{ax + b}}{{cx + d}},;;ad ne bc.$ $left( a right)$ Tập xác định $D = mathbb{R}backslash left{ { – frac{d}{c}} right}$. $left( b right)$ Giới hạn và tiệm cận: $left( b_1 right)$ $mathop {lim }limits_{x to {{left( { – frac{d}{c}} right)}^ pm }} y = mathop {lim }limits_{x to {{left( { – frac{d}{c}} right)}^ pm }} frac{{ax + b}}{{cx + d}} = pm infty Rightarrow x = – frac{d}{c}$ là phương trình của tiệm cận đứng. $left( b_2 right)$ $mathop {lim }limits_{x to pm infty } y = mathop {lim }limits_{x leftrightarrow pm infty } frac{{ax + b}}{{cx + d}} = frac{a}{c} Rightarrow y = frac{a}{c}$ là phương trình của tiệm cận ngang. $left( c right)$ Cực trị: Ta có $y’ = frac{{left| {begin{array}{*{20}{c}} a&b c&d end{array}} right|}}{{{{left( {cx + d} right)}^2}}} = frac{{ad – bc}}{{{{left( {cx + d} right)}^2}}}$ có dấu không đổi nên hàm số không có cực trị. $left( e right)$Trục đối xứng: Giao điểm của hai tiệm cận $Ileft( { – frac{d}{c};frac{a}{c}} right)$ là tâm đối xứng
$left( f right)$ Tính đơn điệu: Tuỳ vào dấu của $y’$ mà tính đơn điệu và đồ thị của hàm nhất biến có $2$ trường hợp sau: $y’ < 0$
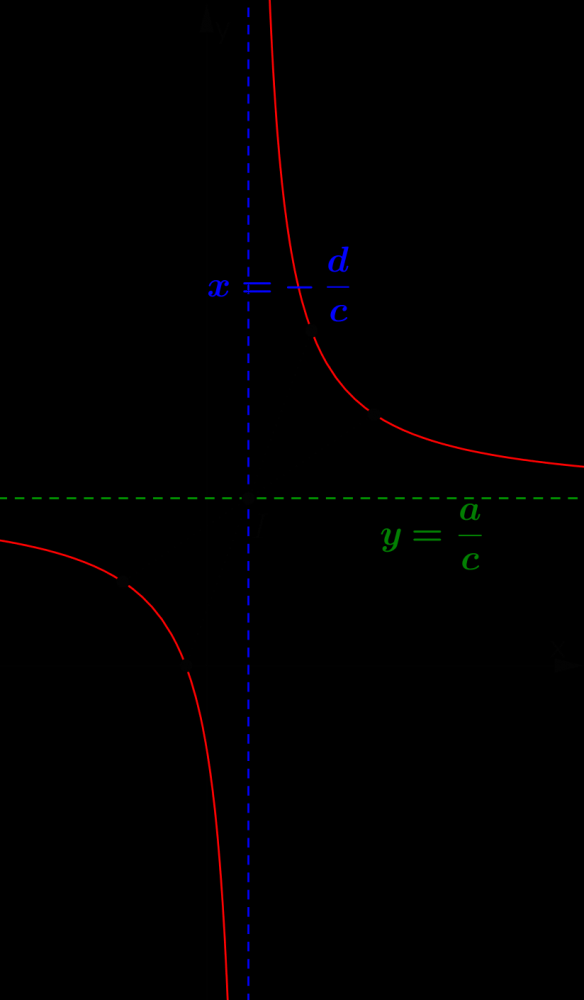
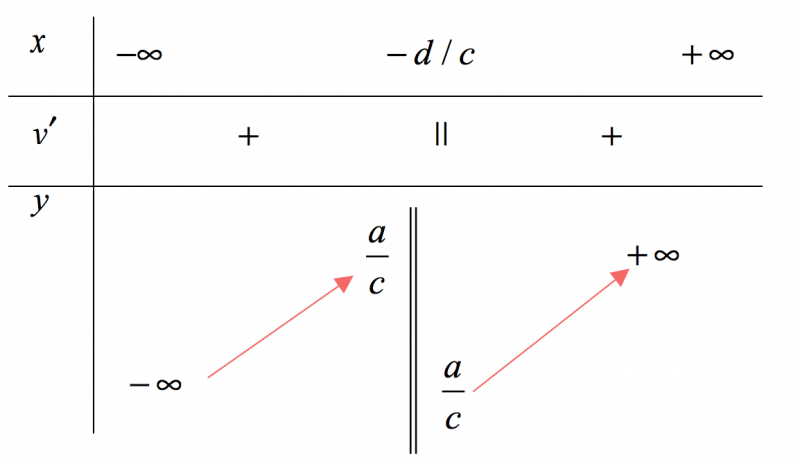
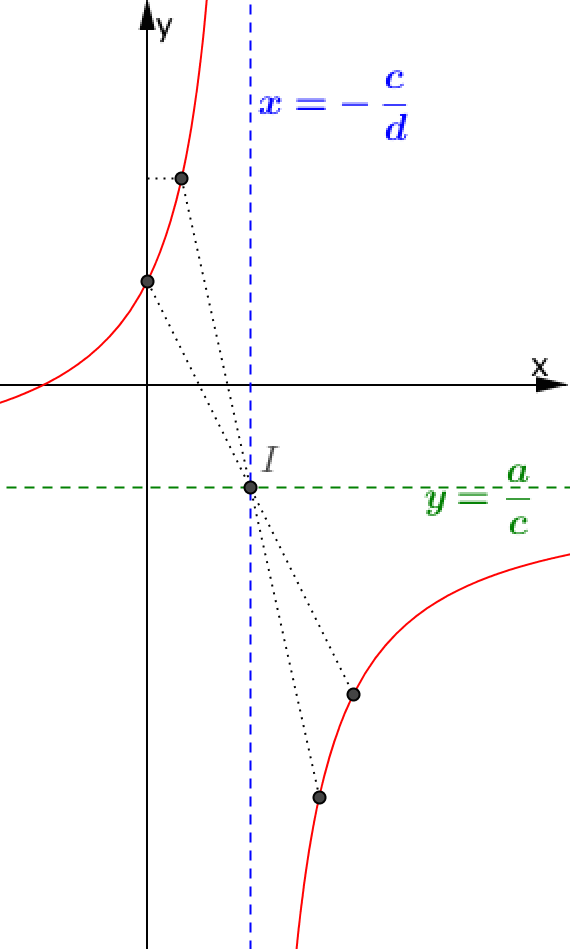
$y’ > 0$
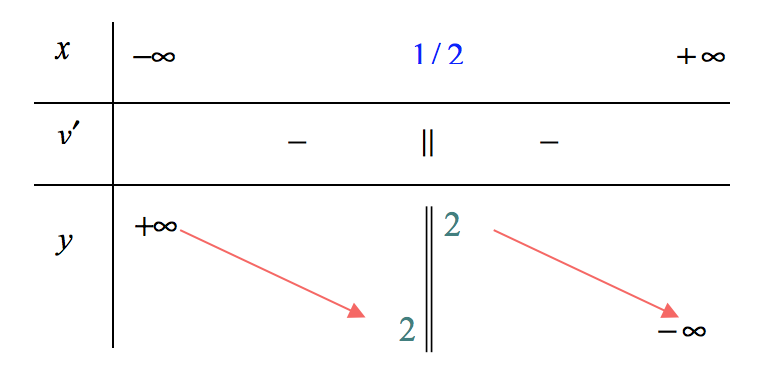
Ví dụ 1. Khảo sát và vẽ đồ thị hàm số $y = frac{{4x + 1}}{{2x -1}}$. Tập xác định $D = mathbb{R}backslash left{{frac{1}{2}} right}.$ $ x = frac{1}{2}$ là phương trình tiệm cận đứng; $ y = 2$ là phương trình tiệm cận ngang. Sự biến thiên: Ta có $y’ = – frac{6}{(2x – 1)^2} < 0$
Suy ra hàm số nghịch biến trên các khoảng xác định. Bảng biến thiên
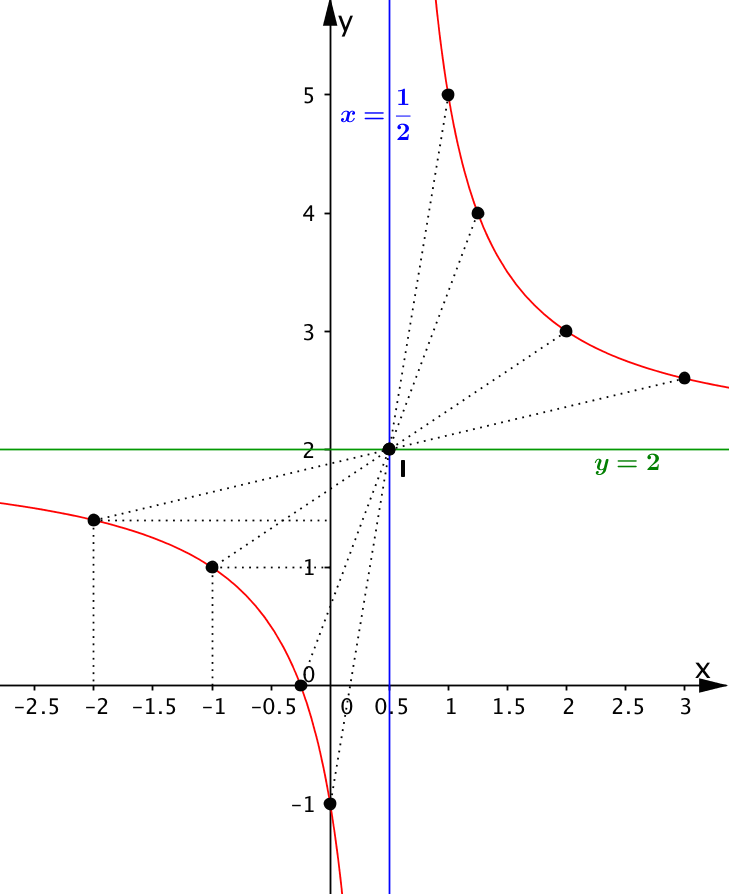
Đồ thị:
Ví Dụ 2: Khảo sát và vẽ đồ thị hàm số (y=frac{2x+1}{x+1}) Giải TXĐ: D = R {-1} (y’=frac{2(x+1)-(2x+1)}{(x+1)^2}=frac{1}{(x+1)^2}) (y’>0 forall xin (-infty ;-1);(-1;+infty )) Khoảng đồng biến ((-infty ;-1);(-1;+infty )) Hàm số không có cực trị. Giới hạn và tiệm cận (lim_{xrightarrow +infty }y=lim_{xrightarrow +infty }frac{2x+1}{x+1 }=lim_{xrightarrow +infty }frac{2+frac{1}{x}}{1+frac{1}{x}}=2) Vậy đường tiệm cận ngang y – 2 = 0. (lim_{xrightarrow infty }y=2) (lim_{xrightarrow -1^- }y=+infty , lim_{xrightarrow -1^+ }y=-infty) Vậy đường tiệm cận đứng x + 1 = 0 Bảng biến thiên 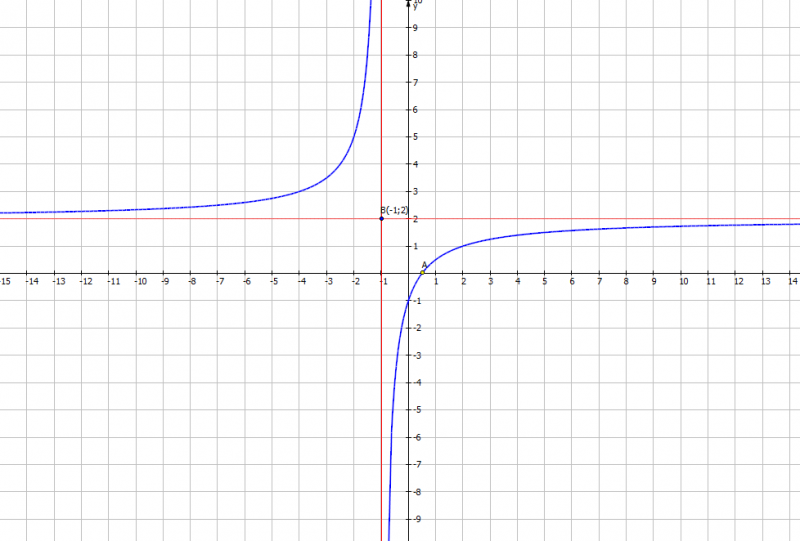 Giao với Ox ((-frac{1}{2};0)) Giao với Oy (0;1) Đồ thị nhận (-1;2) làm tâm đối xứng
Giao với Ox ((-frac{1}{2};0)) Giao với Oy (0;1) Đồ thị nhận (-1;2) làm tâm đối xứng
Ví Dụ 3: Khảo sát sự biến thiên và vẽ đồ thị hàm số (y=frac{-x+3}{x-1}) Giải TXĐ: D = R {1} (y’=frac{-(x-1)-(x+3)}{(x-1)^2}=frac{-2}{(x-1)^2}) (y'<0 forall xin (-infty ;1),(1;+infty )) nên hàm số nghịch biến trên ((-infty ;1),(1;+infty )) Hàm số không có cực trị. Giới hạn: (lim_{xrightarrow -infty }y=lim_{xrightarrow -infty } frac{-x+3}{x-1}=lim_{xrightarrow -infty }frac{-1+frac{3}{x}}{1-frac{1}{x}} =-1) (lim_{xrightarrow +infty }y=lim_{xrightarrow +infty } frac{-x+3}{x-1}=lim_{xrightarrow +infty }frac{-1+frac{3}{x}}{1-frac{1}{x}} =-1) Đường tiệm cận ngang y + 1 = 0 (lim_{xrightarrow 1^-}y=-infty; lim_{xrightarrow 1^+}y=+infty) Đường tiệm cận đứng x – 1 = 0. Bảng biến thiên 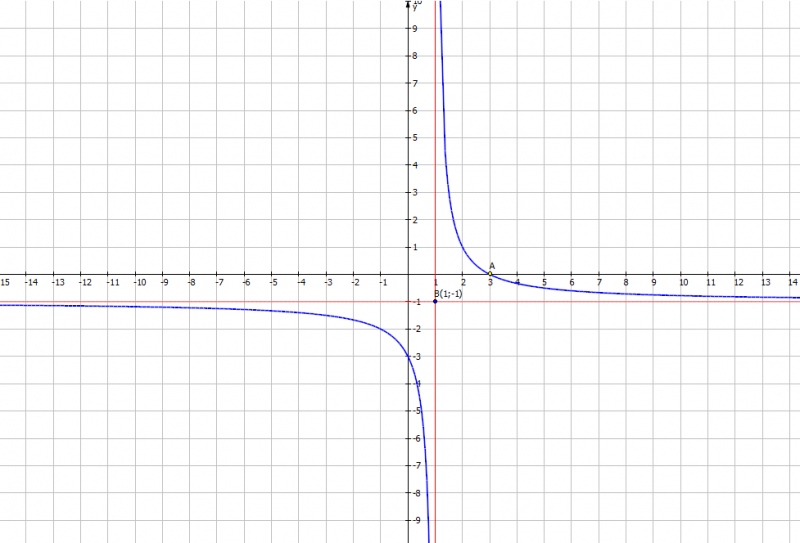 Giao với Ox (3;0) Giao với Oy (0;-3)
Giao với Ox (3;0) Giao với Oy (0;-3)







