1. Định nghĩa khoảng cách giữa 2 đường thẳng chéo nhau
Trong không gian tọa độ Oxyz, có 4 vị trí tương đối của 2 đường thẳng đó là trùng nhau, cắt nhau, chéo nhau và song song. Trong trường hợp 2 đường thẳng chéo nhau, khoảng cách giữa chúng chính là độ dài đoạn vuông góc chung của 2 đường thẳng. Trong đó, đoạn thẳng nối 2 điểm trên 2 đường thẳng chéo nhau, đồng thời vuông góc với cả 2 đường thẳng đó chính là đoạn vuông góc chung.
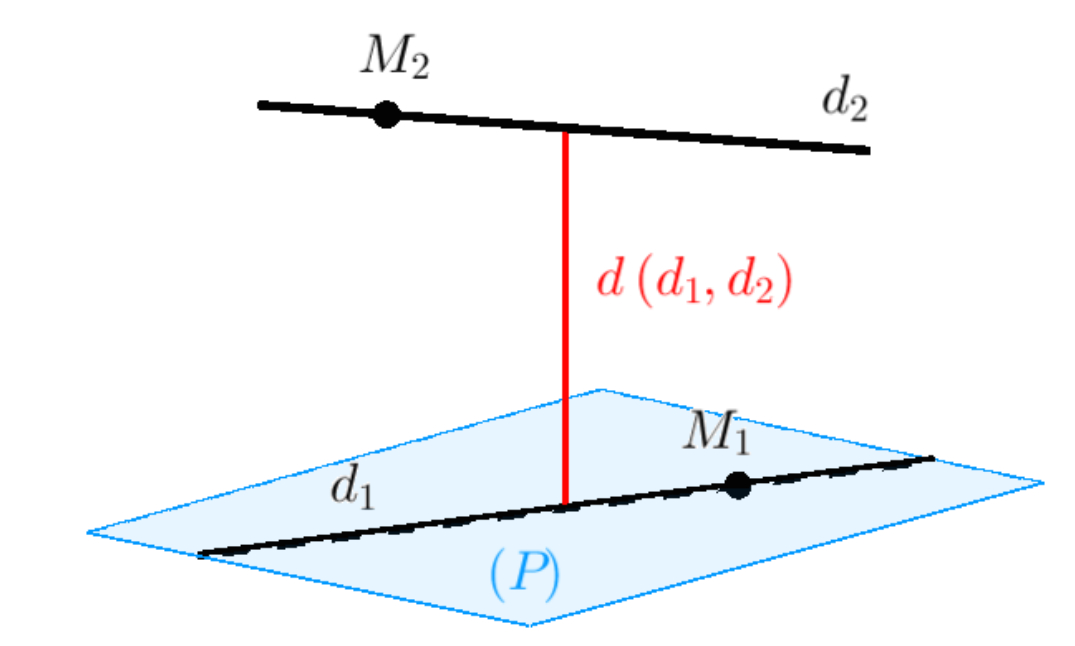
Lưu ý, đoạn vuông góc chung của 2 đường thẳng chéo nhau là chỉ có một, tồn tại duy nhất.
2. Các phương pháp tính khoảng cách 2 đường thẳng chéo nhau
Muốn tính khoảng cách 2 đường thẳng chéo nhau, các em học sinh cần nắm vững các phương pháp như tính khoảng cách từ điểm tới mặt phẳng, cách dựng hình chiếu vuông góc lên mặt phẳng,… Dưới đây là 3 cách tính khoảng cách 2 đường thẳng chéo nhau thường sử dụng để giải các bài toán nhất.
2.1. Phương pháp 1: Dựng đoạn vuông góc chung của hai đường thẳng và tính độ dài đoạn vuông góc chung đó
Đây là phương pháp đơn giản nhất và thường được sử dụng nhất để giải bài tập tính khoảng cách 2 đường thẳng chéo nhau. Các em học sinh áp dụng công thức sau:
Khi 2 đường thẳng a và b đồng thời chéo nhau và vuông góc với nhau, thường sẽ tồn tại một mặt phẳng (
) chứa đường a và vuông góc với đường b. Khi đó, ta dựng đoạn vuông góc chung bằng 2 bước sau:
-
Tìm giao điểm H thỏa mãn thuộc đường thẳng b và nằm trong mặt phẳng (
). -
Tại mặt phẳng (
), ta dựng HK vuông góc với đường thẳng a tại K. Khi đó, HK chính là đoạn vuông góc chung của đường thẳng a và đường thẳng b. Sau đó áp dụng công thức tính khoảng cách để tiến hành tính toán.
Lưu ý, phương pháp 1 chỉ nên sử dụng khi 2 đường thẳng a và đường thẳng b vuông góc với nhau. Khi đó, việc tìm và dựng đường vuông góc chung rất đơn giản. Nhưng nếu 2 đường a và b không vuông góc thì việc dựng đường vuông góc chung rất phức tạp.
Áp dụng phương pháp 1, ta cùng giải một số ví dụ sau đây:
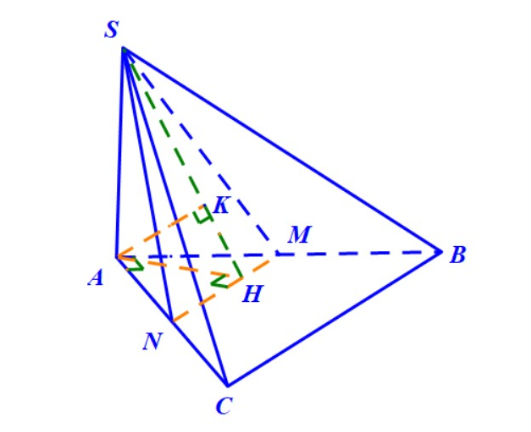
Đăng ký ngay để được các thầy cô ôn tập và tổng hợp kiến thức về hình học không gian ngay!
2.2. Phương pháp 2: Tính khoảng cách từ đường thẳng thứ nhất tới mặt phẳng song song với nó và chứa đường thẳng thứ hai
Khi 2 đường thẳng a và b chéo nhau nhưng không vuông góc với nhau, ta áp dụng cách tính khoảng cách từ đường thẳng thứ nhất tới mặt phẳng song song với nó và chứa đường thẳng thứ hai theo các bước sau đây:
-
Bước 1: Chọn mặt phẳng (α) chứa đường b và song song với đường a.
-
Bước 2: Dựng một đường thẳng d là hình chiếu vuông góc của đường thẳng a xuống mặt phẳng (α) bằng cách lấy điểm M thuộc đường thẳng a dựng đoạn MN vuông góc với mặt phẳng (α). Vậy, đường thẳng d lúc này sẽ đi qua N và song song với a.
-
Bước 3: Gọi H là giao điểm của d và b, từ đó dựng HK song song với MN.
Như vậy, HK là đoạn vuông góc chung của 2 đường thẳng a và đường thẳng b. Độ dài đoạn vuông góc chung chính bằng đoạn MN.
Để hiểu hơn về cách áp dụng, ta cùng xét các ví dụ sau đây:
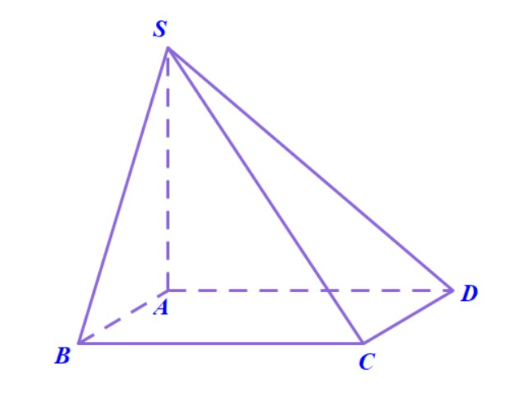
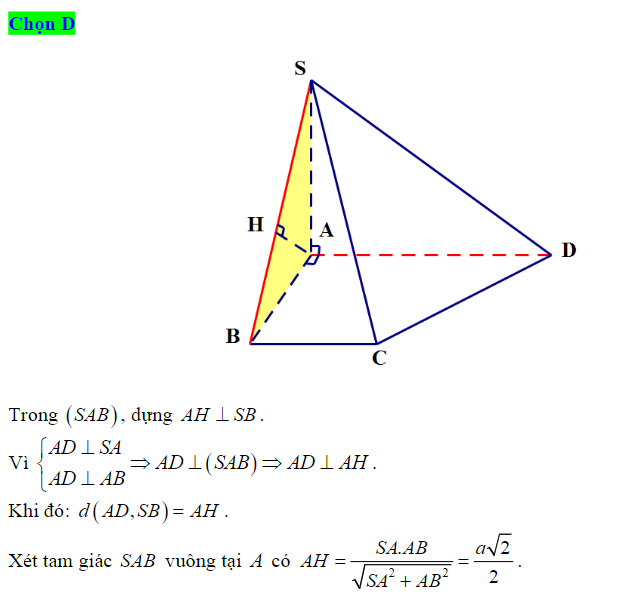
Ví dụ 1 (Câu 40 – đề minh họa THPT Quốc gia 2020): Cho hình chóp S.ABCD. SA vuông góc với đáy là (ABC), SA=a,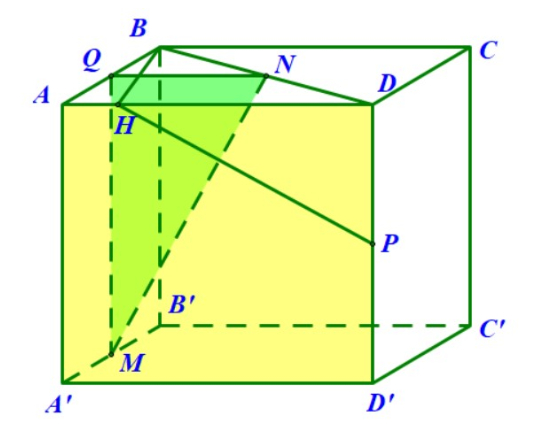 
ABC vuông tại đỉnh A, AC=4a, AB=2a. M là trung điểm của AB. Tính khoảng cách giữa 2 đường SM và BC trong hình.
Giải:
Gọi điểm N là trung điểm của cạnh AC, ta có:
Suy ra:
Vì đường AB cắt mặt phẳng (SMN) tại trung điểm M, nên:
Lần lượt kẻ AHMN và AKSH, áp dụng kết quả hình chóp có 3 tia đồng quy và đôi một vuông góc với nhau, ta có:
Thay số vào ta được .
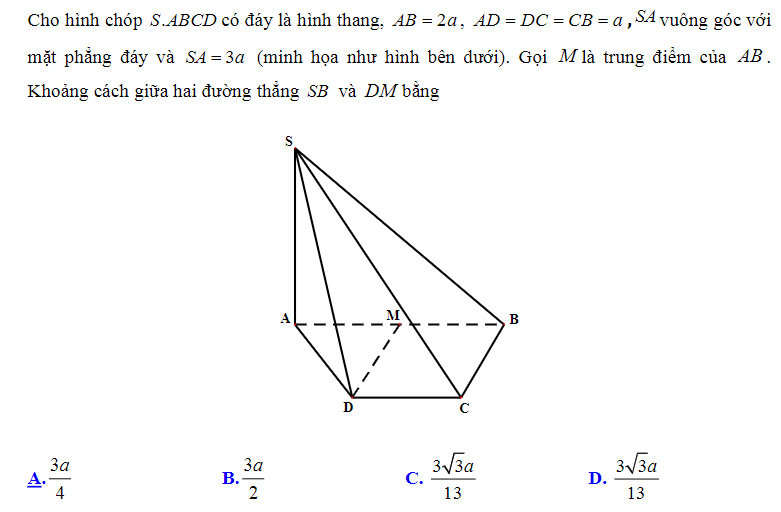
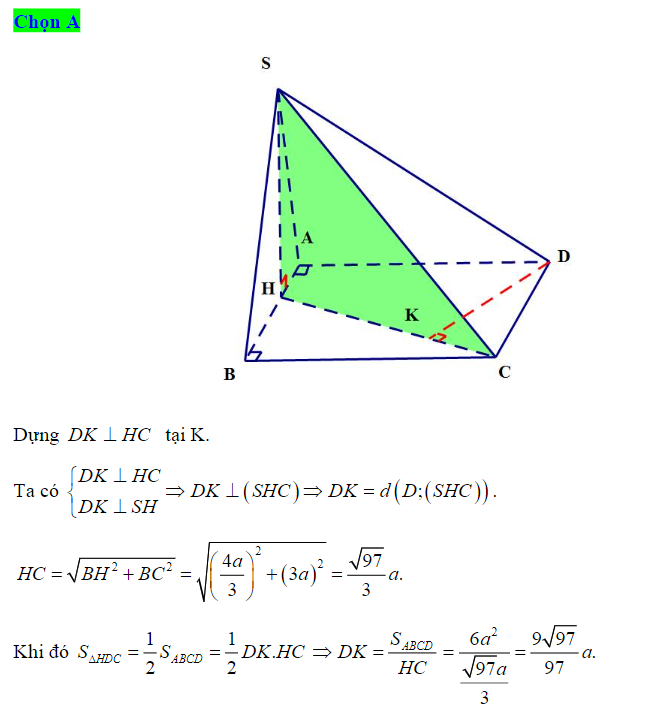
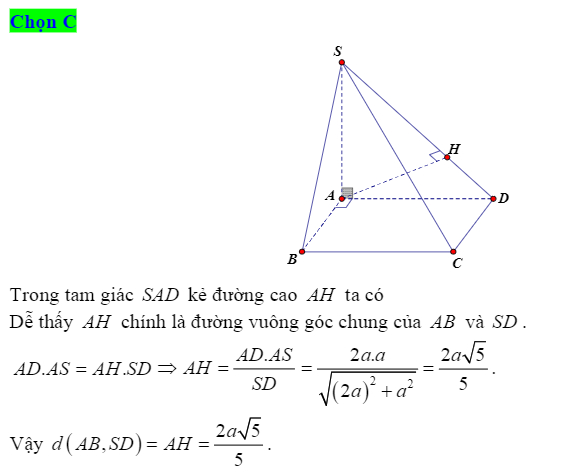
Ví dụ 2: Cho hình chóp S.ABCD có đáy là hình vuông có cạnh bằng a, SA=a, SA vuông góc với đáy. Tính khoảng cách giữa 2 đoạn AB và SC.
Giải:
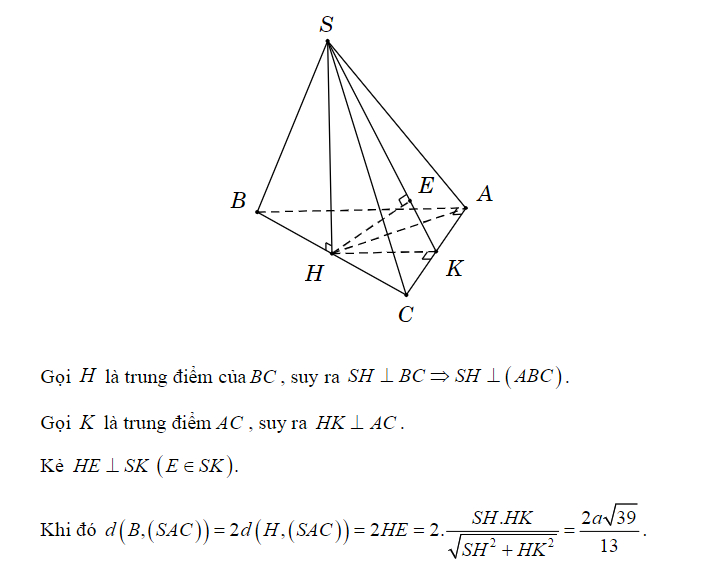
Ta có AB//CD => AB//(SCD). Do đó:
Kẻ đường cao AK thuộc tam giác SAD, ta có khoảng cách cần tìm là:
2.3. Phương pháp 3: Tính khoảng cách giữa hai mặt phẳng song song chứa hai đường thẳng đã cho
Đây là phương pháp tính khoảng cách 2 đường thẳng chéo nhau bằng cách chuyển về tính khoảng cách giữa hai mặt phẳng song song lần lượt chứa 2 đường thẳng đã cho. Công thức chung sẽ là:
Lưu ý: Phương pháp này thường sử dụng trong trường hợp khi kẻ đường thẳng song song với 1 trong 2 đường đề bài cho ban đầu gặp khó khăn.
Các em học sinh cùng VUIHOC xét ví dụ tính khoảng cách sau đây:
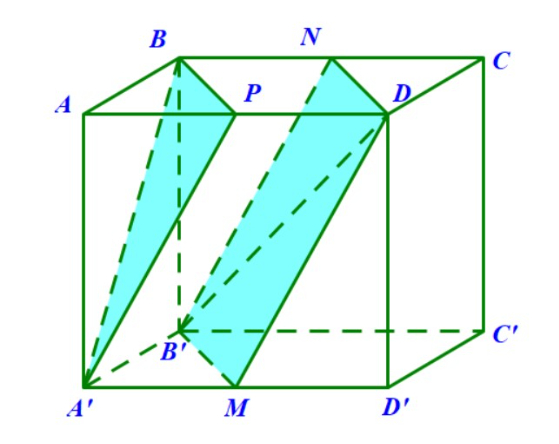
Ví dụ 1 (Đề ĐH khối B năm 2002): Cho hình lập phương cạnh a ABCD.A’B’C’D’. Hãy tính khoảng cách giữa 2 đường thẳng B’D và A’B theo a.
Giải:
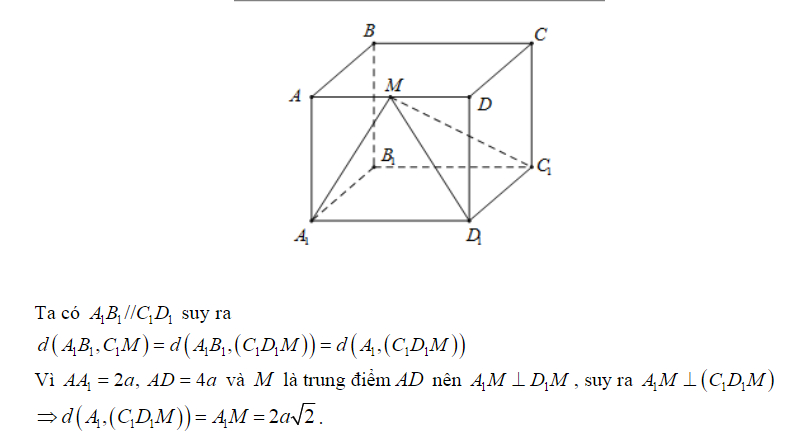
Ví dụ 2: Cho hình hộp đứng ABCD.A’B’C’D’ nhận đáy là hình bình hành với AD=2a, AB=a, góc BAD bằng 60 độ và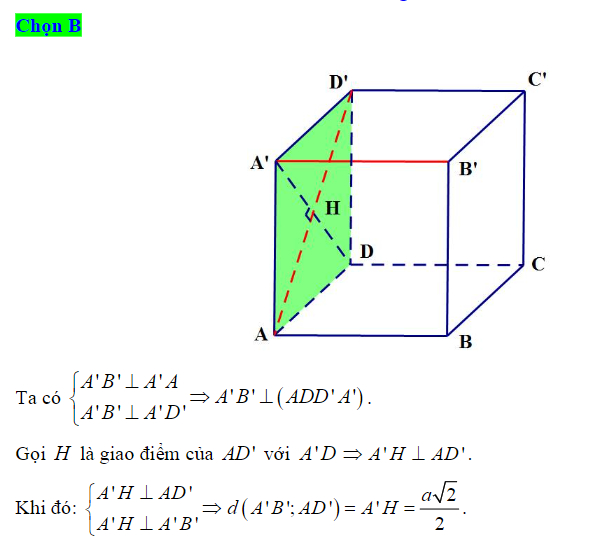 
. Gọi 3 điểm M, N, P lần lượt là trung điểm của các đoạn A’B’, BD và DD’. Hình chiếu vuông góc của B lên AD là H. Hãy tính khoảng cách giữa 2 đường thẳng chéo nhau MN và HP trong hình hộp đó.
Giải:
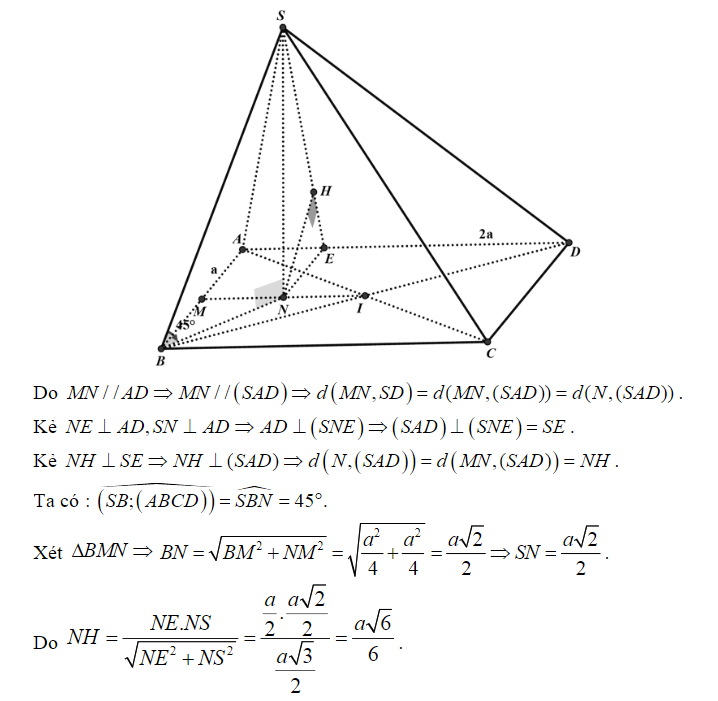
3. Một số bài tập về khoảng cách hai đường thẳng chéo nhau Oxyz
Để luyện tập thành thạo phần kiến thức khoảng cách hai đường thẳng chéo nhau Oxyz, các em cùng VUIHOC giải bài tập về khoảng cách 2 đường thẳng chéo nhau dưới đây nhé!
Bài 1:
Giải:
Vì M là trung điểm của đoạn
Nên tứ giác ADCM và BCDM là hình thoi.
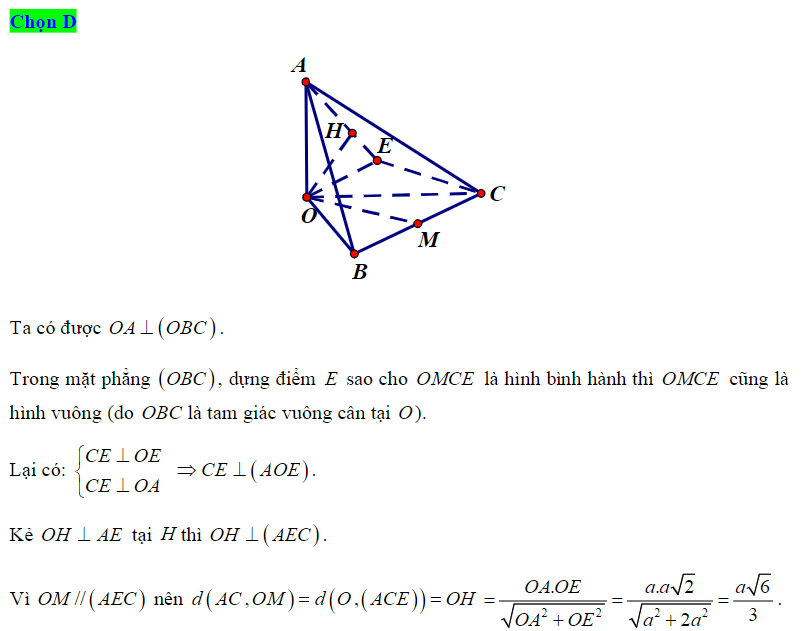
Do
(1)
Ta xét tam giác ABC có đường trung tuyến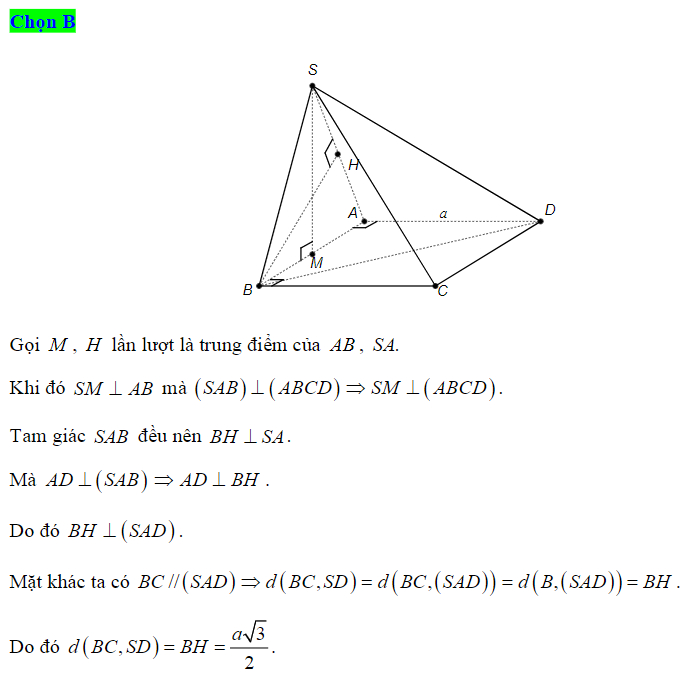 
vuông tại đỉnh
Trong tam giác vuông SAC, ta dựng AHSC.
Xét
Xét thấy tam giác ABC vuông tại C,
Vì tam giác SAC vuông tại A, ta có:
Từ (1) suy ra:
Kết luận:
Bài 2:
Giải:
>>>Đăng ký ngay để được thầy cô xây dựng lộ trình học hình học không gian sao cho hiệu quả và chất lượng nhất<<<
Bài 3:
Giải:
Bài 4:
Giải:
Bài 5:
Giải:
Bài 6:
Giải:
Bài 6:
Giải:
Bài 7:
Giải:
Bài 8:
Giải:
Bài 9:
Giải:
Bài 10:
Giải:
Để ôn lại lý thuyết cũng như thực hành các bài tập về khoảng cách 2 đường thẳng chéo nhau nói riêng và các dạng khoảng cách trong không gian, cùng VUIHOC tham dự bài giảng của thầy Anh Tài trong video sau đây nhé!
Trên đây là toàn bộ kiến thức và phương pháp tính khoảng cách 2 đường thẳng chéo nhau thông dụng nhất trong chương trình THPT – cụ thể là Toán 11. Hy vọng rằng bài viết này sẽ giúp ích cho các em học sinh, đặc biệt là các bạn đang chuẩn bị cho quá trình ôn thi THPT Quốc gia môn Toán năm nay. Để học thêm nhiều kiến thức Toán và các môn khác, truy cập ngay Vuihoc.vn hoặc trung tâm hỗ trợ nhé!
Bài viết tham khảo thêm:
Đường thẳng vuông góc với mặt phẳng
Hai mặt phẳng vuông góc
