Trong chương trình toán 12 nguyên hàm là phần kiến thức đóng vai trò quan trọng, đặc biệt là khi học về hàm số. Ngoài ra, các bài tập về nguyên hàm xuất hiện rất nhiều trong các đề thi THPT QG những năm gần đây. Tuy nhiên, kiến thức về nguyên hàm rất rộng lớn và khá thử thách đối với các bạn học sinh lớp 12. Cùng VUIHOC tìm hiểu và chinh phục các công thức nguyên hàm để dễ dàng hơn trong việc giải các bài tập liên quan nhé!
1. Lý thuyết nguyên hàm
1.1. Định nghĩa nguyên hàm là gì?
Trong chương trình toán giải tích Toán 12 đã học, nguyên hàm được định nghĩa như sau:
Một nguyên hàm của một hàm số thực cho trước f là một F có đạo hàm bằng f, nghĩa là, $F’=f$. Cụ thể:
Cho hàm số f xác định trên K. Nguyên hàm của hàm số f trên K tồn tại khi $F(x)$ tồn tại trên K và $F’(x)=f(x)$ (x thuộc K).
Ta có thể xét ví dụ sau để hiểu hơn về định nghĩa nguyên hàm:
Hàm số $f(x)=cosx$ có nguyên hàm là $F(x)=sinx$ vì $(sinx)’=cosx$ (tức $F’(x)=f(x)$).
2.2. Tính chất của nguyên hàm
Xét hai hàm số liên tục g và f trên K:
- $int [f(x)+g(x)]dx=int f(x)dx+int g(x)dx$
- $int kf(x)dx=kint f(x)$ (với mọi số thực k khác 0)
Ta cùng xét ví dụ dưới đây minh họa cho tính chất của nguyên hàm:
$int sin^{2}xdx=intfrac{1-cos2x}{2}dx=frac{1}{2}int dx-frac{1}{2}int cos2xdx=frac{x}{2}-frac{sin2x}{4}+C$
>> Xem thêm: Cách xét tính liên tục của hàm số, bài tập và ví dụ minh họa
2. Tổng hợp đầy đủ các công thức nguyên hàm dành cho học sinh lớp 12
2.1. Bảng công thức nguyên hàm cơ bản

2.2. Bảng công thức nguyên hàm nâng cao

>>>Cùng thầy cô VUIHOC nắm trọn kiến thức nguyên hàm – Ẵm điểm 9+ thi tốt nghiệp THPT ngay<<<

2.3. Bảng công thức nguyên hàm mở rộng
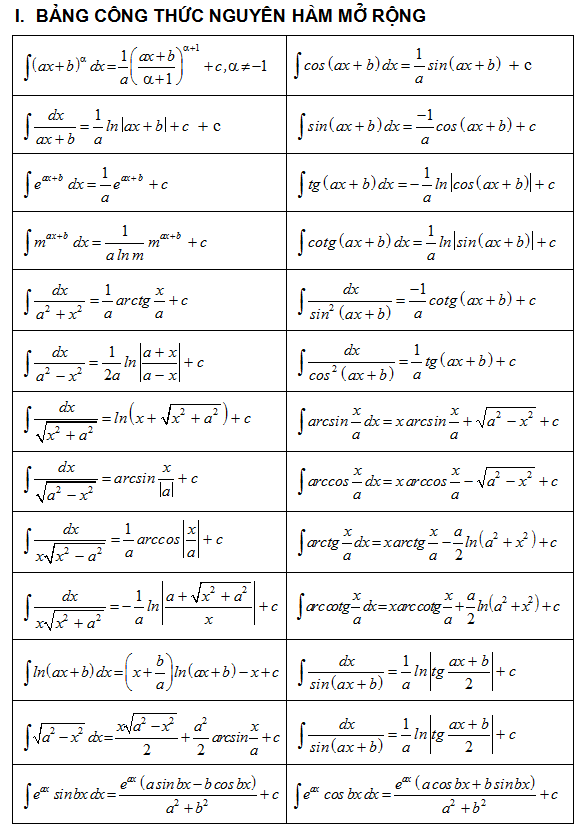
3. Bảng công thức nguyên hàm lượng giác
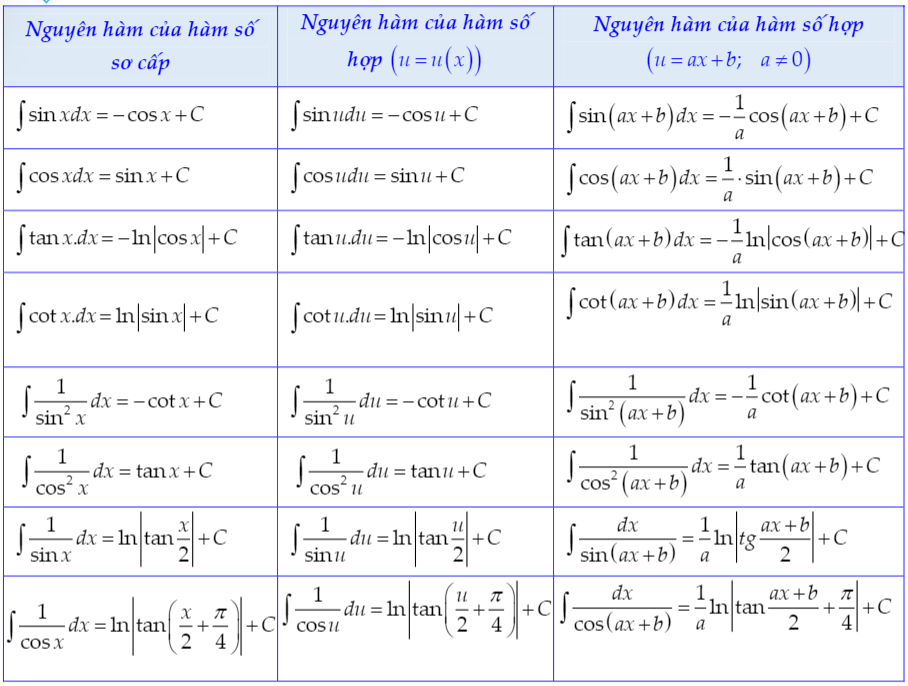
4. Các phương pháp tính nguyên hàm nhanh nhất và bài tập từ cơ bản đến nâng cao
Để dễ dàng hơn trong việc thuộc các công thức nguyên hàm, các em học sinh cần chăm chỉ giải các bài tập áp dụng các phương pháp và công thức nguyên hàm tương ứng. Sau đây, VUIHOC sẽ hướng dẫn các em 4 phương pháp tìm nguyên hàm.
4.1. Công thức nguyên hàm từng phần
Để giải các bài tập áp dụng phương pháp nguyên hàm từng phần, trước tiên học sinh cần nắm được định lý sau:
$int u(x).v'(x)dx=u(x).v(x)-int u(x).u'(x)dx$
Hay $int udv=uv-int vdu$
Với $du=u'(x)dx, dv=v'(x)dx)$
Ta cùng xét 4 trường hợp xét nguyên hàm từng phần (với P(x) là một đa thức theo ẩn x)
Ví dụ minh họa: Tìm họ nguyên hàm của hàm số $int xsinxdx$
Giải:
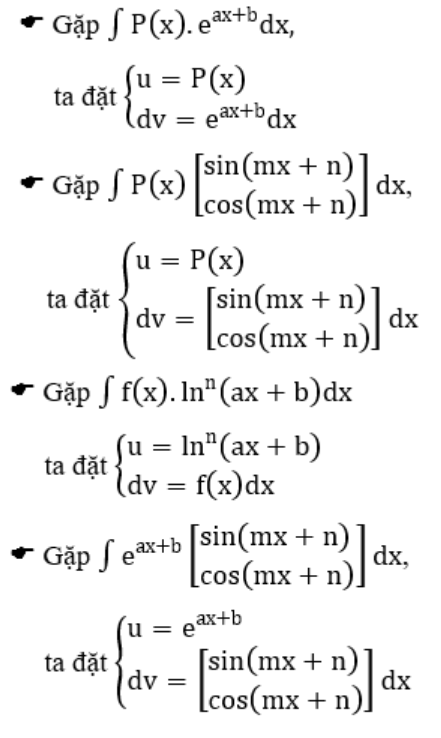
4.2. Phương pháp tính nguyên hàm hàm số lượng giác
Trong phương pháp này, có một số dạng nguyên hàm lượng giác thường gặp trong các bài tập và đề thi trong chương trình học. Cùng VUIHOC điểm qua một số cách tìm nguyên hàm của hàm số lượng giác điển hình nhé!
Dạng 1: $I=int frac{dx}{sin(x+a)sin(x+b)}$
-
Phương pháp tính:
Dùng đồng nhất thức:
$I=int frac{sin(a-b)}{sin(a-b)}=frac{sin[(x+a)-(x+b)]}{sin(a-b)}=frac{sin(x+a)cos(x+b)-cos(x+a)sin(x+b)}{sin(a-b)}$
Từ đó suy ra:
$I=frac{1}{sin(a-b)}int frac{sin(x+a)cos(x+b)-cos(x+a)sin(x+b)}{sin(x+a)sin(x+b)}dx$
$=frac{1}{sin(a-b)}int [frac{cos(x+b)}{sin(x+b)}]-frac{cos(x+a)}{sin(x+a)}]dx$
$=frac{1}{sin(a-b)}[lnsin(x+b)-lnsin(x+a)]+C$
-
Ví dụ áp dụng:
Tìm nguyên hàm sau đây: $I=int frac{dx}{sinxsin(x+frac{pi}{6})}$
Giải:

Dạng 2: $I=int tan(x+a)tan(x+b)dx$
-
Phương pháp tính:
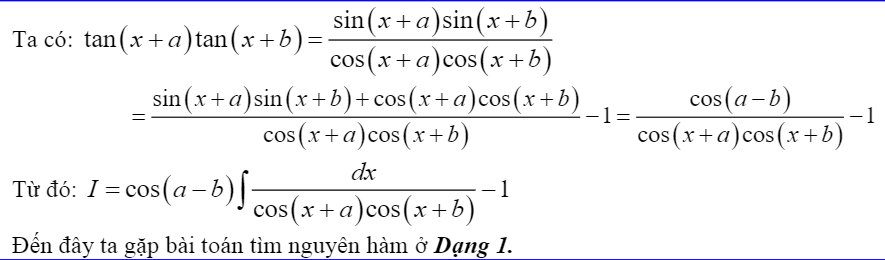
-
Ví dụ áp dụng: Tìm nguyên hàm sau đây: $K=int tan(x+frac{pi}{3}cot(x+frac{pi}{6})dx$
Giải:
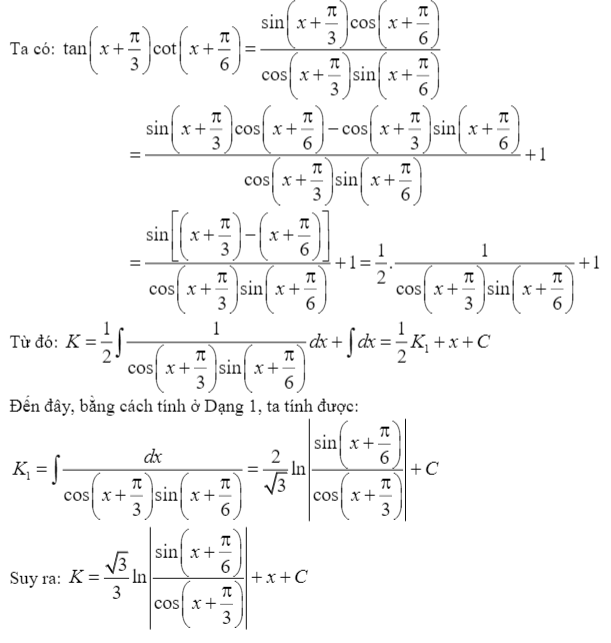
Dạng 3: $I=int frac{dx}{asinx+bcosx}$
-
Phương pháp tính:
-
Ví dụ minh họa: Tìm nguyên hàm I=$int frac{2dx}{sqrt{3}sinx+cosx}$
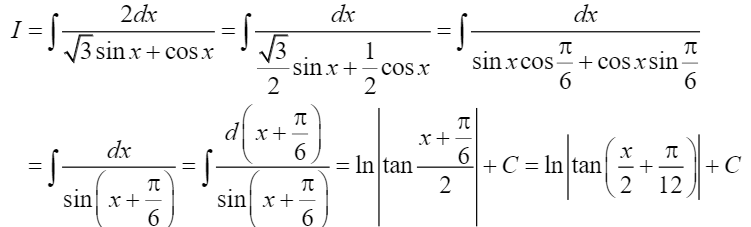
Dạng 4: $I=int frac{dx}{asinx+bcosx+c}$
-
Phương pháp tính:
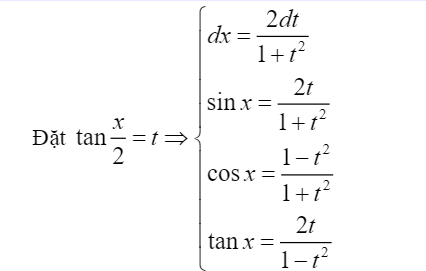
-
Ví dụ áp dụng: Tìm nguyên hàm sau đây: $I=int frac{dx}{3cosx+5sinx+3}$
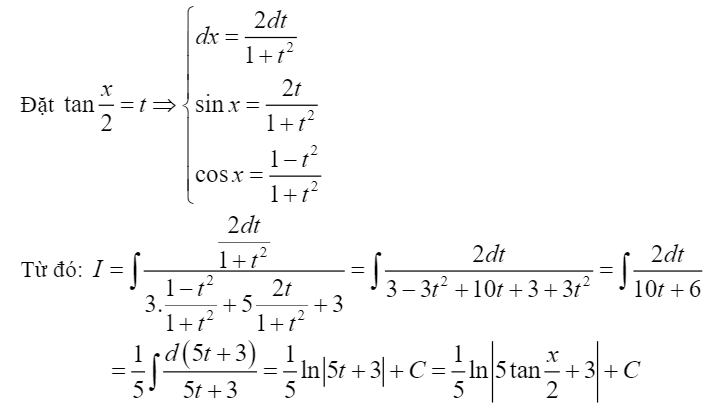

4.3. Cách tính nguyên hàm của hàm số mũ
Để áp dụng giải các bài tập tìm nguyên hàm của hàm số mũ, học sinh cần nắm vững bảng nguyên hàm của các hàm số mũ cơ bản sau đây:

Sau đây là ví dụ minh họa phương pháp tìm nguyên hàm hàm số mũ:
Xét hàm số sau đây: y=$5.7^{x}+x^{2}$
Giải:
Ta có nguyên hàm của hàm số đề bài là:
Chọn đáp án A
4.4. Phương pháp nguyên hàm đặt ẩn phụ (đổi biến số)
Phương pháp đổi biến số có hai dạng dựa trên định lý sau đây:
-
Nếu $int f(x)dx=F(x)+C$ và $u=varphi (x)$ là hàm số có đạo hàm thì $int f(u)du=F(u) + C$
-
Nếu hàm số f(x) liên tục thì khi đặt $x=varphi(t)$ trong đó $varphi(t)$ cùng với đạo hàm của nó $varphi'(t)$ là những hàm số liên tục, ta sẽ được: $int f(x)=int f(varphi(t)).varphi'(t)dt$
Từ phương pháp chung, ta có thể phân ra làm hai bài toán về phương pháp nguyên hàm đặt ẩn phụ như sau:
Bài toán 1: Sử dụng phương pháp đổi biến số dạng 1 tìm nguyên hàm $I=f(x)dx$
Phương pháp:
-
Bước 1: Chọn $x=varphi(t)$, trong đó $varphi(t)$ là hàm số mà ta chọn cho thích hợp
-
Bước 2: Lấy vi phân 2 vế, $dx=varphi'(t)dt$
-
Bước 3: Biển thị $f(x)dx$ theo t và dt: $f(x)dx=f(varphi (t)).varphi’ (t)dt=g(t)dt$
-
Bước 4: Khi đó $I=int g(t)dt=G(t)+C$
Ví dụ minh họa:
Tìm nguyên hàm của $I=int frac{dx}{sqrt{(1-x^{2})^{3}}}$
Giải:
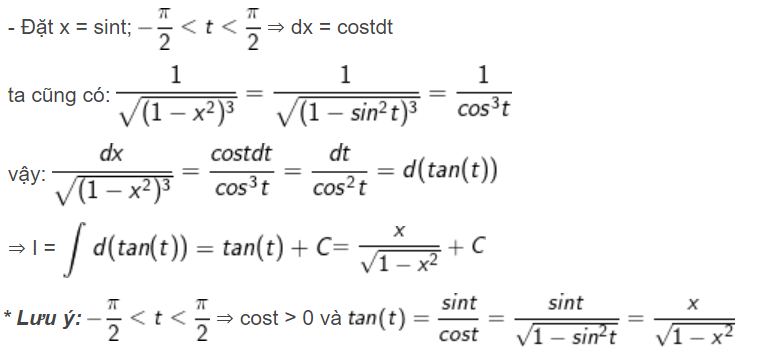
Bài toán 2: Sử dụng phương pháp đổi biến số dạng 2 tìm nguyên hàm $I=int f(x)dx$
Phương pháp:
-
Bước 1: Chọn $t=psi (x)$ trong đó $psi (x)$ là hàm số mà ta chọn cho thích hợp
-
Bước 2: Tính vi phân 2 vế: $dt=psi ‘(x)dx$
-
Bước 3: Biểu thị $f(x)dx$ theo t và dt: $f(x)dx=f[psi (x)].psi'(x)dt=g(t)dt$
-
Bước 4: Khi đó$ I=int g(t)dt=G(t)+C$
Ví dụ minh họa:
Tìm nguyên hàm $I=int x^{3}(2-3x^{2})^{8}dx$
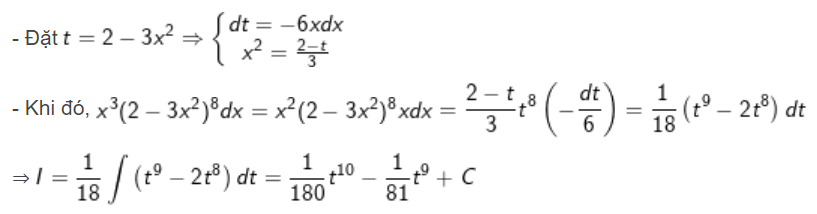
Trên đây là toàn bộ kiến thức cơ bản và tổng hợp đầy đủ công thức nguyên hàm cần nhớ. Hy vọng rằng sau bài viết này, các em học sinh sẽ có thể áp dụng công thức để giải các bài tập nguyên hàm từ cơ bản đến nâng cao. Để học và ôn tập nhiều hơn những phần công thức Toán 12 phục vụ ôn thi THPT QG, truy cập Vuihoc.vn và đăng ký khóa học ngay từ hôm nay nhé!
>> Xem thêm:
- Công thức nguyên hàm lnx và cách giải các dạng bài tập
- Tính nguyên hàm của tanx bằng công thức cực hay
- Phương pháp tính tích phân từng phần và ví dụ minh họa

