Bài viết hướng dẫn phương pháp ứng dụng tích phân để tính thể tích khối tròn xoay khi quay quanh Ox hình phẳng giới hạn bởi ít nhất hai đường cong, đây là dạng toán thường gặp trong chương trình Giải tích 12.
I. MỘT SỐ KẾT QUẢ CẦN LƯU Ý 1. Phương pháp chung Đưa về tổng hoặc hiệu thể tích các khối tròn xoay giới hạn bởi một đường cong và trục $Ox$, quay quanh $Ox.$
2. Chú ý a) Cho hình phẳng giới hạn bởi đồ thị các hàm số $y = f(x)$, $y = g(x)$ liên tục trên đoạn $[a;b]$ ($f(x)g(x) ge 0$, $forall x in [a;b]$) và hai đường thẳng $x = a$, $x = b$ quay quanh $Ox$ ta được khối tròn xoay có thể tích là: $V = pi int_a^b {left| {{f^2}(x) – {g^2}(x)} right|dx} .$ b) Cho hình phẳng giới hạn bởi đồ thị các hàm số $y = f(x)$, $y = g(x)$ liên tục trên đoạn $[alpha ;beta ]$ ($f(x)g(x) ge 0$, $forall x in [alpha ;beta ]$), quay quanh $Ox$ ta được khối tròn xoay có thể tích là: $V = pi int_alpha ^beta {left| {{f^2}(x) – {g^2}(x)} right|dx} $, trong đó $alpha $, $beta $ lần lượt là nghiệm nhỏ nhất và lớn nhất của phương trình $f(x) = g(x).$
3. Có thể vẽ các đồ thị để tìm ra công thức tính thể tích khối tròn xoay tạo thành do hình phẳng giới hạn bởi nhiều đường cong quay quanh $Ox.$ Sau đây là một số ví dụ minh họa về công thức tính thể tích khối tròn xoay do hình phẳng được gạch chéo quay quanh $Ox.$
$V = pi int_a^b {left[ {{f^2}(x) – {g^2}(x)} right]dx} .$
$V = pi int_a^b {left[ {{g^2}(x) – {f^2}(x)} right]dx} .$
$V = pi int_a^b {{g^2}} (x)dx.$
$V = pi int_a^c {left[ {{f^2}(x) – {g^2}(x)} right]dx} $ $ + pi int_c^b {left[ {{g^2}(x) – {f^2}(x)} right]dx} .$
$V = pi int_a^b {{f^2}} (x)dx + pi int_a^b {{g^2}} (x)dx.$
$V = pi int_a^c {left[ {{g^2}(x) – {h^2}(x)} right]dx} $ $ + pi int_c^b {left[ {{f^2}(x) – {h^2}(x)} right]dx} .$
II. BÀI TẬP TRẮC NGHIỆM MINH HỌA Ví dụ 1: Gọi $V$ là thể tích khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi đồ thị hai hàm số $y = f(x)$, $y = g(x)$ và hai đường thẳng $x=a$, $x=b$ (phần gạch chéo trong hình vẽ bên) quay quanh $Ox.$
Khẳng định nào sau đây là đúng? A. $V = int_a^b {[f(x) – g(x)]dx} .$ B. $V = int_a^b {left| {{f^2}(x) – {g^2}(x)} right|dx} .$ C. $V = pi int_a^b {left[ {{f^2}(x) + {g^2}(x)} right]dx} .$ D. $V = pi int_a^b {left[ {{f^2}(x) – {g^2}(x)} right]dx} .$
Lời giải: Từ đồ thị ta có: $V = pi int_a^b {{f^2}} (x)dx – pi int_a^b {{g^2}} (x)dx$ $ = pi int_a^b {left[ {{f^2}(x) – {g^2}(x)} right]dx} .$ Chọn đáp án D.
Ví dụ 2: Gọi $V$ là thể tích khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi đồ thị hai hàm số $y = f(x)$, $y = g(x)$ và hai đường thẳng $x= a$, $x=b$ (phần gạch chéo trong hình vẽ bên) quay quanh $Ox.$
Khẳng định nào sau đây là sai? A. $V = pi int_a^b {left| {{f^2}(x) – {g^2}(x)} right|dx} .$ B. $V = pi int_a^c {left[ {{f^2}(x) – {g^2}(x)} right]dx} $ $ + pi int_c^b {left[ {{g^2}(x) – {f^2}(x)} right]dx} .$ C. $V = pi int_a^c {left| {{f^2}(x) – {g^2}(x)} right|dx} $ $ + pi int_c^b {left| {{f^2}(x) – {g^2}(x)} right|dx.} $ D. $V = pi int_a^b {left[ {{f^2}(x) – {g^2}(x)} right]dx} .$
Lời giải: $V = pi int_a^b {left| {{f^2}(x) – {g^2}(x)} right|dx} $ $ = pi int_a^c {left| {{f^2}(x) – {g^2}(x)} right|dx} $ $ + pi int_c^b {left| {{f^2}(x) – {g^2}(x)} right|dx} .$ $ = pi int_a^c {left| {{f^2}(x) – {g^2}(x)} right|dx} $ $ + pi int_c^b {left| {{f^2}(x) – {g^2}(x)} right|dx} .$ Chọn đáp án C.
Ví dụ 3: Gọi $V$ là thể tích khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi đồ thị hai hàm số $y = f(x)$, $y = g(x)$ và hai đường thẳng $x = a$, $x=b$ (phần gạch chéo trong hình vẽ bên) quay quanh $Ox.$
Khẳng định nào sau đây là đúng? A. $V = pi int_a^b {left| {{f^2}(x) – {g^2}(x)} right|dx} .$ B. $V = pi int_a^b {left[ {{f^2}(x) – {g^2}(x)} right]dx} .$ C. $V = pi int_a^b {{f^2}} (x)dx.$ D. $V = pi int_a^b {{g^2}} (x)dx.$
Lời giải: Từ đồ thị ta suy ra: $V = pi int_a^b {{f^2}} (x)dx.$ Chọn đáp án C.
Ví dụ 4: Gọi $V$ là thể tích khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi đồ thị hai hàm số $y = f(x)$, $y = g(x)$ và trục hoành (phần gạch chéo trong hình vẽ bên) quay quanh $Ox.$
Khẳng định nào sau đây là đúng? A. $V = pi int_a^b {left| {{f^2}(x) – {g^2}(x)} right|dx} .$ B. $V = pi int_a^b {left[ { – {f^2}(x) – {g^2}(x)} right]dx} .$ C. $V = pi int_a^b {left[ {{f^2}(x) – {g^2}(x)} right]dx} .$ D. $V = pi int_a^b {left[ {{f^2}(x) + {g^2}(x)} right]dx} .$
Lời giải: Từ đồ thị ta suy ra: $V = pi int_a^b {{f^2}} (x)dx + pi int_a^b {{g^2}} (x)dx$ $ = pi int_a^b {left[ {{f^2}(x) + {g^2}(x)} right]dx} .$ Chọn đáp án D.
Ví dụ 5: Gọi $V$ là thể tích khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi đồ thị ba hàm số $y = f(x)$, $y = g(x)$, $y = h(x)$ (phần gạch chéo trong hình vẽ bên) quay quanh $Ox.$
Khẳng định nào sau đây là đúng? A. $V = pi int_a^b {left| {{f^2}(x) – {g^2}(x)} right|dx} $ $ + pi int_b^c {left| {{h^2}(x) – {g^2}(x)} right|dx} .$ B. $V = pi int_a^b {left[ {{f^2}(x) – {h^2}(x)} right]dx} $ $ + pi int_b^c {left[ {{h^2}(x) – {g^2}(x)} right]dx} .$ C. $V = pi int_a^b {left[ {{f^2}(x) – {h^2}(x)} right]dx} $ $ + pi int_b^c {left[ {{g^2}(x) – {h^2}(x)} right]dx} .$ D. $V = pi int_a^b {left| {{f^2}(x) – {g^2}(x)} right|dx} $ $ + pi int_b^c {left| {{h^2}(x) – {g^2}(x)} right|dx} .$
Lời giải: Từ đồ thị ta suy ra: $V = pi int_a^b {left[ {{f^2}(x) – {h^2}(x)} right]dx} $ $ + pi int_b^c {left[ {{g^2}(x) – {h^2}(x)} right]dx} .$ Chọn đáp án C.
Ví dụ 6: Thể tích khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi các đường $y = {x^2}$, $y = 4$ quay quanh $Ox$ bằng: A. $V = frac{{64pi }}{5}.$ B. $V = frac{{128pi }}{5}.$ C. $V = frac{{256pi }}{5}.$ D. $V = 32pi .$
Lời giải: Tìm hoành độ giao điểm: ${x^2} = 4 Leftrightarrow x = pm 2.$ Thể tích: Ta có $4{x^2} ge 0$, $forall x in [ – 2;2]$ nên: $V = pi int_{ – 2}^2 {left| {{x^4} – 16} right|dx} = frac{{256pi }}{5}.$ Chọn đáp án C.
Ví dụ 7: Thể tích khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi các đường $y = {e^{2x}}$, $y = {e^x}$, $x = 0$, $x = 1$ quay quanh $Ox$ bằng? A. $V = pi left( {frac{1}{4}{e^4} – frac{1}{2}{e^2} + frac{1}{4}} right).$ B. $V = pi left( {frac{1}{4}{e^4} – frac{1}{2}{e^2}} right).$ C. $V = pi left( {frac{1}{4}{e^4} + frac{1}{2}{e^2} – frac{2}{3}{e^3} + frac{{11}}{{12}}} right).$ D. $V = pi left( {frac{1}{4}{e^4} + frac{1}{2}{e^2} – frac{2}{3}{e^3}} right).$
Lời giải: Ta có: ${e^{2x}}.{e^x} > 0$, $forall x in [0;1].$ ${e^{4x}} = {e^{2x}} Leftrightarrow x = 0.$ Thể tích: $V = pi int_0^1 {left| {{e^{4x}} – {e^{2x}}} right|dx} $ $ = pi left| {int_0^1 {left( {{e^{4x}} – {e^{2x}}} right)dx} } right|.$ $ = pi left| {left. {left( {frac{1}{4}{e^{4x}} – frac{1}{2}{e^{2x}}} right)} right|_0^1} right|$ $ = pi left( {frac{1}{4}{e^4} – frac{1}{2}{e^2} + frac{1}{4}} right).$ Chọn đáp án A.
Ví dụ 8: Thể tích khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi các đường $y = {e^x}$, $y = 2$, $x = 0$ quay quanh $Ox$ bằng? A. $V = pi left( {4ln 2 – frac{5}{2}} right).$ B. $V = pi left( {4ln 2 – frac{3}{2}} right).$ C. $V = pi left( {4ln 2 – frac{1}{2}} right).$ D. $V = 4pi ln 2.$
Lời giải: Tìm hoành độ giao điểm: ${e^x} = 2$ $ Leftrightarrow x = ln 2$, $2.{e^x} > 0$, $forall x in [0;ln 2].$ Thể tích: $V = pi int_0^{ln 2} {left| {4 – {e^{2x}}} right|dx} $ $ = pi left| {int_0^{ln 2} {left( {4 – {e^{2x}}} right)dx} } right|$ $ = pi left| {left. {left( {4x – frac{{{e^{2x}}}}{2}} right)} right|_0^{ln 2}} right|$ $ = pi left( {4ln 2 – frac{3}{2}} right).$ Chọn đáp án B.
Ví dụ 9: Thể tích khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi các đường $y = {e^x}$, $y = 2$, $x = 1$ quay quanh $Ox$ bằng $pi left( {a + bln 2 + frac{{{e^2}}}{c}} right)$ với $a$, $b$, $c$ là các số nguyên. Tính $S=a+2b+c.$ A. $S=-4.$ B. $S=-2.$ C. $S=2.$ D. $S=4.$
Lời giải: Tìm hoành độ giao điểm: ${e^x} = 2$ $ Leftrightarrow x = ln 2.$ $2.{e^x} > 0$, $forall x in [ln 2;1].$ Thể tích: $V = pi int_{ln 2}^1 {left| {4 – {e^{2x}}} right|dx} $ $ = pi left| {int_{ln 2}^1 {left( {4 – {e^{2x}}} right)dx} } right|$ $ = pi left| {left. {left( {4x – frac{{{e^{2x}}}}{2}} right)} right|_{ln 2}^1} right|$ $ = pi left( { – 6 + 4ln 2 + frac{{{e^2}}}{2}} right).$ $ Rightarrow a = – 6$, $b = 4$, $c = 2$ $ Rightarrow S = a + 2b + c = 4.$ Chọn đáp án D.
Ví dụ 10: Thể tích khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi các đường $y = sin x$, $y = cos x$, $x = 0$, $x = frac{pi }{2}$ quay quanh $Ox$ bằng $a + bpi $ với $a$, $b$ là các số nguyên. Tính $S = {b^{2018}} – {a^{2018}} + a + b.$ A. $S=0.$ B. $S=1.$ C. $S=2.$ D. $S=3.$
Lời giải: Tìm hoành độ giao điểm: $left{ {begin{array}{*{20}{l}} {sin x = cos x} {x in left[ {0;frac{pi }{2}} right]} end{array}} right.$ $ Leftrightarrow x = frac{pi }{4}.$ $sin xcos x ge 0$, $forall x in left[ {0;frac{pi }{2}} right].$ Thể tích: $V = pi int_0^{frac{pi }{2}} {left| {{{cos }^2}x – {{sin }^2}x} right|dx} $ $ = pi int_0^{frac{pi }{2}} | cos 2x|dx.$ $ = pi left| {int_0^{frac{pi }{4}} {cos } 2xdx} right| + pi left| {int_{frac{pi }{4}}^{frac{pi }{2}} {cos } 2xdx} right|$ $ = pi left| {left. {frac{{sin 2x}}{2}} right|_0^{frac{pi }{4}}} right| + pi left| {left. {frac{{sin 2x}}{2}} right|_{frac{pi }{4}}^{frac{pi }{2}}} right| = pi .$ $ Rightarrow a = 0$, $b = 1$ $ Rightarrow S = {b^{2018}} – {a^{2018}} + a + b = 2.$ Chọn đáp án C.
Ví dụ 11: Thể tích khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi các đường $y = {sin ^2}x$, $y = {cos ^2}x$, $x = 0$, $x = frac{pi }{8}$ quay quanh $Ox$ bằng $frac{a}{b}pi sqrt 2 $ với $a$, $b$ là các số nguyên dương và $frac{a}{b}$ là phân số tối giản. Tính $S = {a^2} + 3b.$ A. $S=7.$ B. $S=11.$ C. $S=12.$ D. $S=13.$
Lời giải: Tìm hoành độ giao điểm: $left{ {begin{array}{*{20}{l}} {{{sin }^2}x = {{cos }^2}x} {x in left[ {0;frac{pi }{8}} right]} end{array}} right.$ $ Leftrightarrow x in emptyset .$ ${sin ^2}x.{cos ^2}x ge 0$, $forall x in left[ {0;frac{pi }{8}} right].$ Thể tích: $V = pi int_0^{frac{pi }{8}} {left| {{{cos }^4}x – {{sin }^4}x} right|dx} $ $ = pi left| {int_0^{frac{pi }{8}} {cos } 2xdx} right|$ $ = pi left| {left. {frac{{sin 2x}}{2}} right|_0^{frac{pi }{8}}} right|$ $ = frac{{pi sqrt 2 }}{4}.$ $ Rightarrow a = 1$, $b = 4$ $ Rightarrow S = {a^2} + 3b = 13.$ Chọn đáp án D.
Ví dụ 12: Thể tích khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi các đường $y = {x^2}$, $y = x + 2$ quay quanh $Ox$ bằng $frac{a}{b}pi $ với $a$, $b$ là các số nguyên dương và $frac{a}{b}$ là phân số tối giản. Tính $S = a – {b^3}.$ A. $S=-22.$ B. $S=-1.$ C. $S=1.$ D. $S=22.$
Lời giải: Tìm hoành độ giao điểm: ${x^2} = x + 2$ $ Leftrightarrow left[ {begin{array}{*{20}{l}} {x = – 1} {x = 2} end{array}} right..$ ${x^2}(x + 2) ge 0$ $forall x in [ – 1;2].$ Thể tích: $V = pi int_{ – 1}^2 {left| {{x^4} – {{(x + 2)}^2}} right|dx} = frac{{72}}{5}pi $ $ Rightarrow a = 72$, $b = 5$ $ Rightarrow S = a – 2{b^2} = 22.$ Chọn đáp án D.
Ví dụ 13: Thể tích khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi các đường $x = {y^2}$, $y = x$ quay quanh $Ox$ bằng $frac{a}{b}pi $ với $a$, $b$ là các số nguyên dương và $frac{a}{b}$ là phân số tối giản. Tính khoảng cách $h$ từ điểm $M(a;b)$ đến đường thẳng $Delta 😡 + y – 3 = 0.$ A. $h = sqrt 2 .$ B. $h = frac{{3sqrt 2 }}{2}.$ C. $h = 2sqrt 2 .$ D. $h = frac{{5sqrt 2 }}{2}.$
Lời giải: Tìm hoành độ giao điểm: ${x^2} = x$ $ Leftrightarrow left[ {begin{array}{*{20}{l}} {x = 0} {x = 1} end{array}} right..$
Thể tích: $V = pi int_0^1 {left( {x – {x^2}} right)dx} $ $ = frac{1}{6}pi .$ $ Rightarrow a = 1$, $b = 6$ $ Rightarrow M(1;6).$ $ Rightarrow d(M;Delta )$ $ = frac{{|1 + 6 – 3|}}{{sqrt {{1^2} + {1^2}} }} = 2sqrt 2 .$ Chọn đáp án C.
Ví dụ 14: Thể tích khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi các đường $y = {x^2}$, $y = 2sqrt {2x} $ quay quanh $Ox$ bằng $frac{a}{b}pi $ với $a$, $b$ là các số nguyên dương và $frac{a}{b}$ là phân số tối giản. Tính khoảng cách từ điểm $M(a;b)$ đến điểm $N(50;2).$ A. $MN = 1763.$ B. $MN = sqrt {1763} .$ C. $MN = 13.$ D. $MN = sqrt {13} .$
Lời giải: Tìm hoành độ giao điểm: ${x^2} = 2sqrt {2x} $ $ Leftrightarrow left[ {begin{array}{*{20}{l}} {x = 0} {x = 2} end{array}} right..$ ${x^2}2sqrt {2x} ge 0$, $forall x in [0;2].$ Thể tích: $V = pi int_0^2 {left| {{x^4} – 8x} right|dx} = frac{{48}}{5}pi .$ $ Rightarrow a = 48$, $b = 5$ $ Rightarrow M(48;5).$ $ Rightarrow MN$ $ = sqrt {{{(50 – 48)}^2} + {{(2 – 5)}^2}} $ $ = sqrt {13} .$ Chọn đáp án D.
Ví dụ 15: Thể tích khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi các đường $y = 2sqrt x $, $y = x$ quay quanh $Ox$ bằng $frac{a}{b}pi $ với $a$, $b$ là các số nguyên dương và $frac{a}{b}$ là phân số tối giản. Tính $T = a – {b^3}.$ A. $T=-19.$ B. $T =-5.$ C. $T=5.$ D. $T=19.$
Lời giải: Tìm hoành độ giao điểm: $2sqrt x = x$ $ Leftrightarrow left{ {begin{array}{*{20}{l}} {x ge 0} {4x = {x^2}} end{array}} right.$ $ Leftrightarrow left[ {begin{array}{*{20}{l}} {x = 0} {x = 4} end{array}} right..$ $x.2sqrt x ge 0$, $forall x in [0;4].$ Thể tích: $V = pi int_0^4 {left| {4x – {x^2}} right|dx} $ $ = frac{{32}}{3}pi $ $ Rightarrow a = 32$, $b = 3.$ $ Rightarrow T = a – {b^3} = 5.$ Chọn đáp án C.
Ví dụ 16: Thể tích khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi các đường $y = {x^2} + 1$, trục tung và tiếp tuyến của đồ thị hàm số $y = {x^2} + 1$ tại điểm có hoành độ bằng $1$ quay quanh $Ox$ bằng $frac{a}{b}pi $ với $a$, $b$ là các số nguyên dương và $frac{a}{b}$ là phân số tối giản. Tính $T= a+b+ ab -45.$ A. $T=-35.$ B. $T = 35.$ C. $T=-98.$ D. $T=98.$
Lời giải: Tìm phương trình tiếp tuyến: ${x_0} = 1$ $ Rightarrow y(1) = 2$ $y'(1) = 2$ suy ra phương trình tiếp tuyến là $y = 2x.$ Tìm hoành độ giao điểm: ${x^2} + 1 = 2x$ $ Leftrightarrow x = 1.$ $left( {{x^2} + 1} right).2x ge 0$, $forall x in [0;1].$ Thể tích: $V = pi int_0^1 {left| {{{left( {{x^2} + 1} right)}^2} – 4{x^2}} right|dx} $ $ = frac{8}{{15}}pi .$ $ Rightarrow a = 8$, $b = 15$ $ Rightarrow T = a + b + ab – 45 = 98.$ Chọn đáp án D.
Ví dụ 17: Thể tích khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi các đường $y = {x^2}$, $y = x$ quay quanh $Ox$ bằng $frac{a}{b}pi $ với $a$, $b$ là các số nguyên dương và $frac{a}{b}$ là phân số tối giản. Tính $T= 3a + b.$ A. $T = 47.$ B. $T=21.$ C. $T=19.$ D. $T=9.$
Lời giải: Tìm hoành độ giao điểm: ${x^2} = x$ $ Leftrightarrow left[ {begin{array}{*{20}{l}} {x = 0} {x = 1} end{array}.} right.$ ${x^2}.x ge 0$, $forall x in [0;1].$ Thể tích: $V = pi int_0^1 {left| {{x^4} – {x^2}} right|dx} = frac{2}{{15}}pi .$ $ Rightarrow a = 2$, $b = 15$ $ Rightarrow T = 3a + b = 21.$ Chọn đáp án B.
Ví dụ 18: Thể tích khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi các đường $y = {x^2}$, $x = {y^2}$ và trục hoành quay quanh $Ox$ bằng $frac{a}{b}pi $ với $a$, $b$ là các số nguyên dương và $frac{a}{b}$ là phân số tối giản. Tính $T= 2a+b.$ A. $T = 23.$ B. $T=16.$ C. $T=7.$ D. $T=5.$
Lời giải: Tìm hoành độ giao điểm: $x = {x^4}$ $ Leftrightarrow left[ {begin{array}{*{20}{l}} {x = 0} {x = 1} end{array}} right..$
Thể tích: $V = pi int_0^1 {left( {x – {x^4}} right)dx} = frac{3}{{10}}pi .$ $ Rightarrow a = 3$, $b = 10$ $ Rightarrow T = 2a + b = 16.$ Chọn đáp án B.
Ví dụ 19: Thể tích khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi các đường $y = sqrt {4x} $, $y = 3 – x$, $y = 0$ quay quanh $Ox$ bằng $frac{m}{n}pi $ với $m$, $n$ là các số nguyên dương và $frac{m}{n}$ là phân số tối giản. Điểm $I(m;n)$ là tâm đối xứng của đồ thị hàm số nào sau đây? A. $y = frac{{14x + 3}}{{x – 3}}.$ B. $y = frac{{x – 3}}{{14x + 1}}.$ C. $y = frac{{3x + 2}}{{x – 14}}.$ D. $y = frac{{3 – x}}{{x – 14}}.$
Lời giải: Tìm hoành độ giao điểm: $sqrt {4x} = 3 – x$ $ Leftrightarrow left{ {begin{array}{*{20}{l}} {3 – x ge 0} {4x = {{(3 – x)}^2}} end{array}} right.$ $ Leftrightarrow x = 1.$ $sqrt {4x} = 0 Leftrightarrow x = 0.$ $3 – x = 0 Leftrightarrow x = 3.$
Thể tích: $V = pi int_0^1 4 xdx + pi int_1^3 {{{(3 – x)}^2}} dx$ $ = frac{{14}}{3}pi .$ $ Rightarrow m = 14$, $n = 3$ $ Rightarrow I(14;3).$ Ta biết đồ thị hàm số $y = frac{{ax + b}}{{cx + d}}$ $(c ne 0,ad – cb ne 0)$ có tâm đối xứng có tọa độ $left( { – frac{d}{c};frac{a}{c}} right).$ $ Rightarrow I(14;3)$ là tâm đối xứng của đồ thị hàm số $y = frac{{3x + 2}}{{x – 14}}.$ Chọn đáp án C.
Ví dụ 20: Thể tích khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi các đường $y = sqrt x $, $y = x – 2$ và trục hoành quay quanh $Ox$ bằng $frac{a}{b}pi $ với $a$, $b$ là các số nguyên dương và $frac{a}{b}$ là phân số tối giản. Tính $T=a+b.$ A. $T = 19.$ B. $T=17.$ C. $T=15.$ D. $T = 13.$
Lời giải: Tìm hoành độ giao điểm: $sqrt x = x – 2$ $ Leftrightarrow left{ {begin{array}{*{20}{l}} {x – 2 ge 0} {x = {{(2 – x)}^2}} end{array}} right.$ $ Leftrightarrow x = 4.$ $sqrt x = 0$ $ Leftrightarrow x = 0.$ $x – 2 = 0$ $ Leftrightarrow x = 2.$
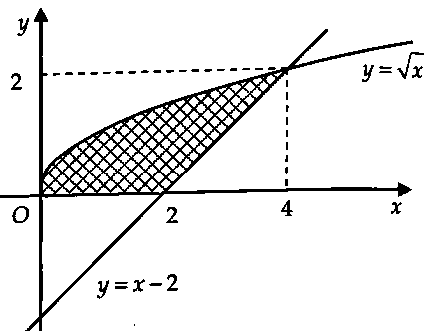
Thể tích: Cách 1: $V = pi int_0^4 x dx – pi int_2^4 {{{(x – 2)}^2}} dx$ $ = frac{{16}}{3}pi .$ Cách 2: $V = pi int_0^2 x dx + pi int_2^4 {left[ {x – {{(x – 2)}^2}} right]dx} $ $ = frac{{16}}{3}pi .$ $ Rightarrow a = 16$, $b = 3$ $ Rightarrow T = a + b = 19.$ Chọn đáp án A.
Ví dụ 21: Thể tích khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi đồ thị $(C)$ của hàm số $y = 3x – {x^2}$ và các tiếp tuyến của đồ thị $(C)$ tại giao điểm của $(C)$ với trục hoành quay quanh $Ox$ bằng $frac{a}{b}pi $ với $a$, $b$ là các số nguyên dương và $frac{a}{b}$ là phân số tối giản. Tính $T=a+b.$ A. $T = 263.$ B. $T = 283.$ C. $T = 293.$ D. $T=303.$
Lời giải: Viết các tiếp tuyến: $3x – {x^2} = 0$ $ Leftrightarrow left[ {begin{array}{*{20}{l}} {x = 0} {x = 3} end{array}} right..$ $x = 0$, $y(0) = 0$, $y'(0) = 3$, phương trình tiếp tuyến là $y = 3x.$ $x = 3$, $y(3) = 0$, $y'(1) = – 3$, phương trình tiếp tuyến là $y = – 3x + 9.$ Tìm các hoành độ giao điểm: $3x – {x^2} = 3x Leftrightarrow x = 0.$ $3x – {x^2} = – 3x + 9 Leftrightarrow x = 3.$ $3x = – 3x + 9 Leftrightarrow x = frac{3}{2}.$
Thể tích: $V = pi int_0^3 {left[ {{{(3x)}^2} – {{left( {3x – {x^2}} right)}^2}} right]dx} $ $ + pi int_2^3 {left[ {{{( – 3x + 9)}^2} – {{left( {3x – {x^2}} right)}^2}} right]dx} $ $ = frac{{243}}{{20}}pi .$ $ Rightarrow a = 243$, $b = 20$ $ Rightarrow T = a + b = 263.$ Chọn đáp án A.
Ví dụ 22: Thể tích khối tròn xoay tạo thành khi cho hình elip $(E):frac{{{x^2}}}{{16}} + frac{{{y^2}}}{4} = 1$ quay quanh $Ox$ bằng $frac{a}{b}pi $ với $a$, $b$ là các số nguyên dương và $frac{a}{b}$ là phân số tối giản. Tính $T= a+b+ 2ab.$ A. $T = 259.$ B. $T = 255.$ C. $T = 250.$ D. $T = 240.$
Lời giải: Tìm hoành độ giao điểm: $frac{{{x^2}}}{{16}} + frac{{{0^2}}}{4} = 1 Leftrightarrow x = pm 4.$
Thể tích: $V = 2pi int_0^4 {frac{{16 – {x^2}}}{4}dx} = frac{{64}}{3}pi .$ $ Rightarrow a = 64$, $b = 3$ $ Rightarrow T = a + b + 2ab = 259.$ Chọn đáp án A.
Ví dụ 23: Thể tích khối tròn xoay tạo thành khi cho hình elip $(E):frac{{{x^2}}}{{{a^2}}} + frac{{{y^2}}}{{{b^2}}} = 1$ $(a > b > 0)$ quay quanh $Ox$ bằng: A. ${frac{{4pi a{b^2}}}{3}.}$ B. ${frac{{4pi {a^2}b}}{3}.}$ C. ${frac{{2pi {a^2}b}}{3}.}$ D. ${frac{{2pi a{b^2}}}{3}.}$
Lời giải: Tìm hoành độ giao điểm: $frac{{{x^2}}}{{{a^2}}} + frac{{{0^2}}}{{{b^2}}} = 1 Leftrightarrow x = pm a.$
Thể tích: $V = 2pi int_0^a {frac{{{b^2}}}{{{a^2}}}} left( {{a^2} – {x^2}} right)dx.$ $ = left. {frac{{2pi {b^2}}}{{{a^2}}}left( {{a^2}x – frac{{{x^3}}}{3}} right)} right|_0^a$ $ = frac{{4pi a{b^2}}}{3}.$ Chọn đáp án A.
Ví dụ 24: Gọi $H$ là hình phẳng giới hạn bởi elip $(E):frac{{{x^2}}}{{16}} + frac{{{y^2}}}{9} = 1$ và parabol $(P):y = frac{{sqrt 7 }}{{12}}{x^2}$ (phần gạch chéo trong hình vẽ bên).
Thể tích khối tròn xoay tạo thành khi cho hình $H$ quay quanh $Ox$ bằng? A. $V = frac{{783pi }}{{40}}.$ B. $V = frac{{783pi }}{{20}}.$ C. $V = frac{{873pi }}{{40}}.$ D. $V = frac{{873pi }}{{20}}.$
Lời giải: Tìm hoành độ giao điểm: $frac{{{x^2}}}{{16}} + frac{{frac{{7{x^4}}}{{144}}}}{9} = 1 Leftrightarrow x = pm 3.$ Thể tích: $V = 2pi int_0^3 {left[ {frac{9}{{16}}left( {16 – {x^2}} right) – frac{{7{x^4}}}{{144}}} right]dx} $ $ = frac{{783}}{{20}}pi .$ Chọn đáp án B.
Ví dụ 25: Gọi $H$ là hình phẳng giới hạn bởi đường tròn và đường elip được gạch chéo trong hình bên.
Thể tích khối tròn xoay tạo thành khi cho hình $H$ quay quanh $Ox$ bằng? A. $V = frac{{320pi }}{3}.$ B. $V = frac{{160pi }}{3}.$ C. $V = frac{{80pi }}{3}.$ D. $V = frac{{40pi }}{3}.$
Lời giải: Tìm phương trình các đường: + Đường tròn tâm $O$, bán kính bằng $5$ nên có phương trình: ${x^2} + {y^2} = 25.$ + Đường elip có phương trình $frac{{{x^2}}}{{25}} + frac{{{y^2}}}{9} = 1.$ Thể tích: $V = 2pi int_0^5 {left[ {left( {25 – {x^2}} right) – frac{{9left( {25 – {x^2}} right)}}{{25}}} right]dx} $ $ = frac{{320}}{3}pi .$ Chọn đáp án A.
Ví dụ 26: Gọi $H$ là hình phẳng giới hạn parabol và trục hoành cho bởi hình bên.
Thể tích khối tròn xoay tạo thành khi cho hình $H$ quay quanh $Ox$ bằng? A. $V = frac{{512pi }}{{15}}.$ B. $V = frac{{256pi }}{{15}}.$ C. $V = frac{{128pi }}{{15}}.$ D. $V = frac{{64pi }}{{15}}.$
Lời giải: Tìm phương trình đường parabol: Gọi parabol $(P):y = a{x^2} + bx + c$ $(a ne 0).$ $(P)$ có đỉnh là $I(0;4)$ và đi qua điểm $A(2;0)$ suy ra: $left{ {begin{array}{*{20}{l}} {c = 4} { – frac{b}{{2a}} = 0} {4a + 2b + c = 0} end{array}} right.$ $ Leftrightarrow left{ {begin{array}{*{20}{l}} {c = 4} {b = 0} {a = – 1} end{array}} right.$ $ Rightarrow (P):y = 4 – {x^2}.$ Thể tích: $V = pi int_{ – 2}^2 {{{left( {4 – {x^2}} right)}^2}} dx = frac{{512pi }}{{15}}.$ Chọn đáp án A.
Ví dụ 27: Gọi $H$ là hình phẳng giới hạn bởi đường tròn và đường parabol được gạch chéo trong hình bên.
Thể tích khối tròn xoay tạo thành khi cho hình $H$ quay quanh $Ox$ bằng? A. $V = frac{{25pi }}{3}.$ B. $V = frac{{50pi }}{3}.$ C. $V = frac{{100pi }}{3}.$ D. $V = frac{{200pi }}{3}.$
Lời giải: Tìm phương trình các đường: + Đường tròn tâm $O$, bán kính bằng $5$ nên có phương trình: ${x^2} + {y^2} = 25.$ + Đường parabol $(P):y = a{x^2} + bx + c$ đỉnh là $I(0;5)$ và đi qua điểm $A(5;0)$ suy ra: $left{ {begin{array}{*{20}{l}} {c = 4} { – frac{b}{{2a}} = 0} {25a + 5b + c = 0} end{array}} right.$ $ Leftrightarrow left{ {begin{array}{*{20}{l}} {c = 4} {b = 0} {a = – frac{1}{5}} end{array}} right.$ $ Rightarrow (P):y = 5 – frac{{{x^2}}}{5}.$ Thể tích: $V = 2pi int_0^5 {left[ {left( {25 – {x^2}} right) – {{left( {5 – frac{{{x^2}}}{5}} right)}^2}} right]dx} $ $ = frac{{100}}{3}pi .$ Chọn đáp án C.
Ví dụ 28: Gọi $H$ là hình phẳng giới hạn bởi đường elip và đường parabol được gạch chéo trong hình bên.
Thể tích khối tròn xoay tạo thành khi cho hình $H$ quay quanh $Ox$ bằng? A. $V = 3pi .$ B. $V = 6pi .$ C. $V = 12pi .$ D. $V = 24pi .$
Lời giải: Tìm phương trình các đường: + Đường elip có phương trình: $frac{{{x^2}}}{{25}} + frac{{{y^2}}}{9} = 1.$ + Đường parabol $(P):y = a{x^2} + bx + c$ đỉnh là $I(0; – 3)$ và đi qua điểm $A(5;0)$ suy ra: $left{ {begin{array}{*{20}{l}} {c = – 3} { – frac{b}{{2a}} = 0} {25a + 5b + c = 0} end{array}} right.$ $ Leftrightarrow left{ {begin{array}{*{20}{l}} {c = – 3} {b = 0} {a = frac{3}{{25}}} end{array}} right.$ $ Rightarrow (P):y = frac{{3{x^2}}}{{25}} – 3.$ Thể tích: $V = 2pi int_0^5 {left[ {frac{9}{{25}}left( {25 – {x^2}} right) – {{left( {frac{{3{x^2}}}{{25}} – 3} right)}^2}} right]dx} $ $ = 12pi .$ Chọn đáp án C.
Ví dụ 29: Một cái trống trường có bán kính các đáy là $30$ $cm$, thiết diện vuông góc với trục và cách đều hai đáy có diện tích là $1600pi $ $left( {c{m^2}} right)$, chiều dài của trống là $1$ $m.$ Biết rằng mặt phẳng chứa trục cắt mặt xung quanh của trống là các đường Parabol. Hỏi thể tích của cái trống là bao nhiêu $d{m^3}$? A. $425,2.$ B. $425162.$ C. $212,6.$ D. $212581.$
Lời giải: Chọn hệ trục $Oxy$ như hình vẽ.
Thiết diện vuông góc với trục và cách đều hai đáy là hình tròn có bán kính $r$ có diện tích là $1600pi $ $c{m^2}.$ $ Rightarrow {r^2}pi = 1600pi $ $ Rightarrow r = 40$ $cm.$ Ta có: Parabol có đỉnh $I(0;40)$ và qua $A(50;30).$ Nên có phương trình $y = – frac{1}{{250}}{x^2} + 40.$ Thể tích của trống là: $V = pi int_{ – 50}^{50} {{{left( { – frac{1}{{250}}{x^2} + 40} right)}^2}} dx$ $ = pi frac{{406000}}{3}$ $c{m^3}$ $ approx 425,2$ $d{m^3}.$ Chọn đáp án A.
Ví dụ 30: Một khối cầu có bán kính bằng $5$ $dm$, người ta cắt bỏ hai đầu bằng hai mặt phẳng cùng vuông góc với một đường kính của khối cầu và cách tâm khối cầu một khoảng bằng $4$ $dm$ để làm một chiếc lu đựng nước. Thể tích cái lu bằng bao nhiêu $d{m^3}$? A. $frac{{500pi }}{3}.$ B. $frac{{2296pi }}{{15}}.$ C. $frac{{952pi }}{{27}}.$ D. $frac{{472pi }}{3}.$
Lời giải: Chọn hệ trục $Oxy$ như hình vẽ.
Phương trình đường tròn nhận hai trục tọa độ làm trục đối xứng: ${x^2} + {y^2} = 25.$ Thể tích của chiếc lu là: $V = pi int_{ – 4}^4 {left( {25 – {x^2}} right)dx} $ $ = frac{{472pi }}{3}$ $d{m^3}.$ Chọn đáp án D.

