1. Hệ tọa độ trong không gian
Trong không gian cho ba trục tọa độ chung gốc (O), đôi một vuông góc với nhau (x’Ox ; y’Oy ; z’Oz). Hệ ba trục tọa độ như vậy được gọi là hệ trục tọa độ Đề-các vuông góc (Oxyz); (O) là gốc tọa tọa độ. Giả sử (overrightarrow{i},overrightarrow{j},overrightarrow{k}) lần lượt là các vectơ đơn vị trên các trục (x’Ox, y’Oy, z’Oz) (h. 52)
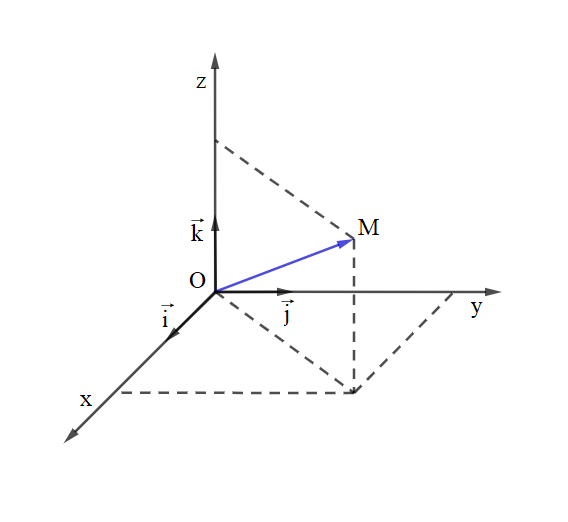
Với điểm (M) thuộc không gian (Oxyz) thì tồn tại duy nhất bộ số ((x ; y ; z)) để
(overrightarrow{OM}= x.overrightarrow{i}+y.overrightarrow{j}+z.overrightarrow{k}),
bộ ((x ; y ; z)) được gọi là tọa độ của điểm (M(x ; y ; z)).
Trong không gian Oxyz cho vectơ (overrightarrow{a}), khi đó (overrightarrow{a}= a_{1}overrightarrow{i}+a_{2}overrightarrow{j}+a_{3}overrightarrow{k})
Ta viết (overrightarrow{a})(({a_1};{a_2};{a_3})) và nói (overrightarrow{a}) có tọa độ (({a_1};{a_2};{a_3})) .
2. Biểu thức tọa độ của các phép toán vectơ
Giả sử (overrightarrow{a})= (({a_1};{a_2};{a_3})) và (overrightarrow{b}) = (({b_1};{b_2};{b_3})), thì:
(overrightarrow{a}+overrightarrow{b}) (= ({a_{1;}} + {b_1};{a_2}; + {rm{ }}{b_2};{rm{ }}{a_3} + {b_3};).)
(overrightarrow{a} – overrightarrow{b}) ( = ({a_{1;}} – {b_1};{a_2}; – {rm{ }}{b_2};{rm{ }}{a_3} – {b_3};).)
( k.overrightarrow{a}) ( = (k{a_1};k{a_2};k{a_3}).)
3. Tích vô hướng
Cho (overrightarrow{a})(({a_1};{a_2};{a_3})) và (overrightarrow{b}) (({b_1};{b_2};{b_3})) thì tích vô hướng (overrightarrow{a}).(overrightarrow{b}) ( = ;{a_1}.{b_1}; + {rm{ }}{a_2}.{b_2}; + {rm{ }}{a_3}.{b_3})
Ta có: (|overrightarrow{a}|=sqrt{a_{1}^{2}+a_{2}^{2}+a_{3}^{2}}.)
Đặt (varphi =left (widehat{overrightarrow{a},overrightarrow{b}} right )) , 0 ≤ (varphi) ≤ 1800 thì (cosvarphi =dfrac{a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3} }{sqrt{a_{1}^{2}+a_{2}^{2}+a_{3}^{2}}sqrt{b_{1}^{2}+b_{2}^{2}+b_{3}^{2}}}) (với (overrightarrow{a}) ≠ (overrightarrow{0}), (overrightarrow{b})≠ (overrightarrow{0}))
4. Phương trình mặt cầu
Trong không gian (Oxyz), mặt cầu ((S)) tâm (I(a ; b ; c)) bán kính (R) có phương trình chính tắc [{left( {x – a} right)^{2;}} + {left( {y-b} right)^2} + {left( {z-c} right)^2}; = {R^2}]
Mặt cầu có phương trình tổng quát ({x^2} + {y^2} + {z^2} + 2ax + 2by + 2cz + d = 0) có tâm (Ileft( { – a; – b; – c} right)) và bán kính (R = sqrt {{a^2} + {b^2} + {c^2} – d} )







