1. Những kiến thức ôn thi toán vào 10 trọng tâm cần ghi nhớ
1.1 Căn thức đại số
– Điều kiện để căn thức có nghĩa: có nghĩa khi A 0
– Các công thức biến đổi căn thức:

1.2 Hàm số
a. Hàm số y = ax + b (a 0)
– Tính chất: Hàm số y = ax + b (a 0) đồng biến trên R khi a > 0; nghịch biến trên R khi a < 0.
– Đồ thị: Đồ thị hàm số y = ax + b (a 0) là một đường thửng đi qua điểm A(0;b); B(-b/a;0).
b. Hàm số y = ax2 (a 0)
– Tính chất:
+ Nếu a > 0 hàm số y = ax2 (a 0) nghịch biến khi x < 0 và đồng biến khi x > 0.
+ Nếu a < 0 hàm số y = ax2 (a 0) đồng biến khi x < 0 và nghịch biến khi x > 0
– Đồ thị: Đồ thị hàm số y = ax2 (a 0) là một đường cong Parabol đi qua gốc tọa độ O (0;0)/
+ Nếu a > 0 thì đồ thị hàm số nằm phía trên trục hoành.
+ Nếu a < 0 thì đồ thị hàm số nằm phía dưới trục hoành.
1.3 Vị trí tương đối của đường thẳng
a. Vị trí tương đối của hai đường thẳng:
Xét đường thẳng y = ax + b (d) và y = a’x + b’ (d’)
(d) và (d’) cắt nhau a a’
(d) // (d’) a = a’ và b b’
(d) (d’) a = a’ và b = b’
(d) (d’) a.a’ = -1
b. Vị trí tương đối của đường thẳng và đường cong
Xét đường thẳng y = ax + b (d) và y = ax2 (P)
(d) và (P) cắt nhau tại hai điểm
(d) tiếp xúc với (P) tại một điểm
(d) và (P) không có điểm chung
1.4 Phương trình bậc hai
Xét phương trình bậc hai ax2 + bx + c = 0 (a 0)
Công thức nghiệm Công thức nghiệm thu gọn
Nếu > 0: Phương trình có hai nghiệm phân biệt:
Nếu = 0: Phương trình có nghiệm kép:
Nếu < 0: Phương trình vô nghiệm.
với b = 2b’
Nếu ‘ > 0: Phương trình có hai nghiệm phân biệt:
Nếu ‘ = 0: Phương trình có nghiệm kép:
Nếu ‘ < 0: Phương trình vô nghiệm.
1.5 Hệ thức Viet và ứng dụng
a. Hệ thức Viet:
– Nếu x1; x2 là nghiệm của phương trình bậc hai ax2 + bx + c = 0 (a 0) thì:
b. Ứng dụng của hệ thức viet:
– Tìm hai số u và v biết u + v = S; u.v = P ta giải phương trình sau: x2 – Sx + P = 0 (Đk: S2 – 4P > 0)
– Nhẩm nghiệm của phương trình bậc hai ax2 + bx + c = 0 (a 0):
Nếu a + b + c = 0 thì phương trình có 2 nghiệm
Nếu a – b + c = 0 thì phương trình có 2 nghiệm:
>> Kinh nghiệm ôn thi vào 10 môn toán giúp đạt điểm cao
1.6 Hệ thức lượng trong tam giác vuông
b2 = ab’
c2 = ac’
h2 = b2 + c2
1.7 Tỉ số lượng giác của góc nhọn
0 < sin < 1 ; 0 < cos < 1
1.8 Hệ thức về cạnh trong tam giác vuông
b = asinB = acosC
b = ctgB = ccotgC
c = asinC = acosB
c = btgC = bcotgB
1.9 Đường tròn
– Cách xác định: Qua ba điểm không thẳng hàng, ta vẽ được một và chỉ một đường tròn.
– Tâm đối xứng, trục đối xứng: Đường tròn có một tâm đối xứng và có vô số trục đối xứng.
– Quan hệ vuông góc giữa đường kính và dây trong một đường tròn:
+ Đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.
+ Đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy.
– Liên hệ giữa dây và khoảng cách từ tâm đến dây trong một đường tròn:
+ Hai dây bằng nhau thì cách đều tâm.
+ Hai dây cách đều tâm thì bằng nhau.
+ Dây nào lớn hơn thì dây đó gần tâm hơn.
+ Dây nào gần tâm hơn thì dây đó lớn hơn.
– Liên hệ giữa dây và cung trong một đường tròn hay trong hai đường tròn bằng nhau:
+ Hai cung bằng nhau căng hai dây bằng nhau.
+ Hay dây bằng nhau căng hai cung bằng nhau.
+ Cung lớn hơn căng dây lớn hơn.
+ Dây lớn hơn căng cung lớn hơn.
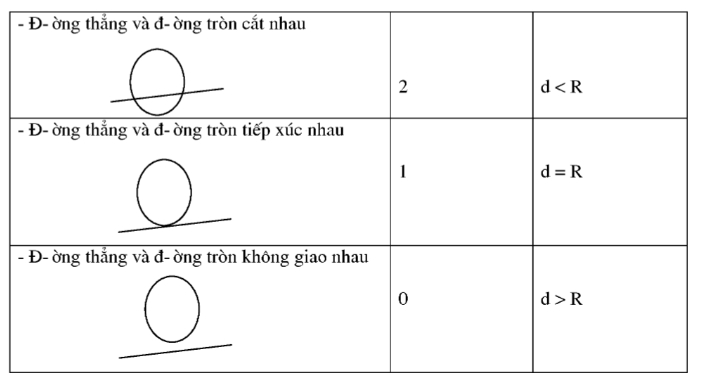
– Vị trí tương đối của đường thẳng và đường tròn:
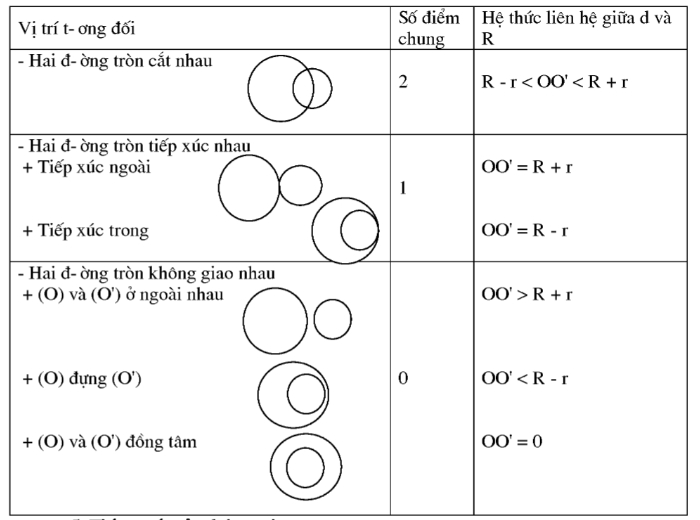
– Vị trí tương đối của hai đường tròn:
– Độ dài đường tròn, độ dài cung tròn:
+ Độ dài đường tròn bán kính R: C = 2R = d
+ Độ dài cung tròn no bán kính R:
– Diện tích hình tròn, diện tích hình quạt tròn:
+ Diện tích hình tròn: S = R2
+ Diện tích hình quạt tròn bánh kính R, cong no:
– Các loại đường tròn:
1.10 Tiếp tuyến của đường tròn
– Tính chất của tiếp tuyến: Tiếp tuyến vuông góc với bán kính đi qua tiếp điểm.
– Dấu hiệu nhận biết tiếp tuyến:
+ Đường thẳng và đường tròn chỉ có một điểm chung.
+ Khoảng cách từ tâm của đường tròn đến đường thẳng bằng bán kính.
+ Đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó.
– Tính chất của hai tiếp tuyến cắt nhau:
MA và MB là hai tiếp tuyến cắt nhau thì:
+ MA = MB
+ MO là phân giác của góc AMB
+ OM là phân giác của góc AOB
– Tiếp tuyến chung của hai đường tròn: Là đường thẳng tiếp xúc với cả hai đường tròn đó
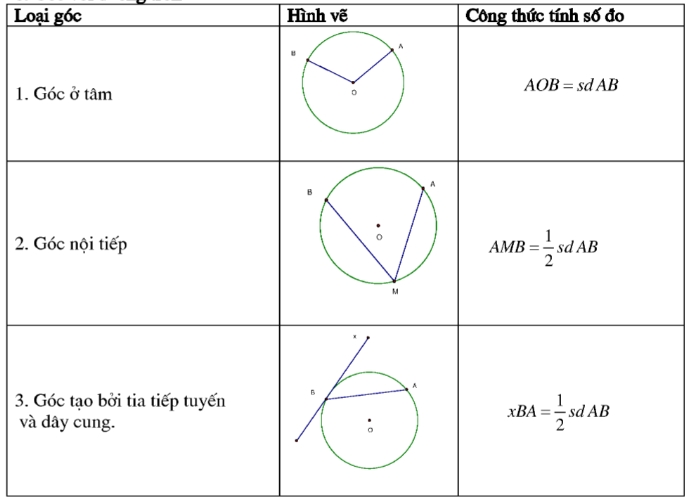
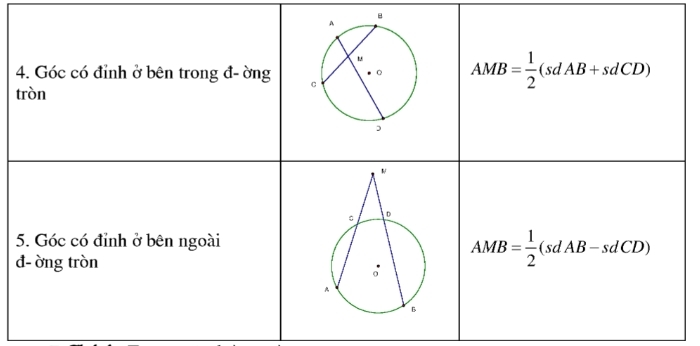
1.11 Góc với đường tròn
1.12 Các loại hình trong không gian
Hình trụ Hình nón Hình nón cụt Hình cầu Diện tích xung quanh Sxq = 2 Sxq = 2 Sxq =(r1 + r2)l S = 4R2=d Diện tích toàn phần Stp = 2 + Stp = 2 + Thể tích hình trụ V = Sh =
Khóa học trực tuyến ôn thi vào 10 mới nhất của nhà trường VUIHOC giúp các em vững bước vào 10. Đăng ký ngay để nhận tài liệu ôn thi được biên soạn bởi thầy cô đến từ trường chuyên TOP 5 toàn quốc.
2. Những dạng bài thường gặp trong đề thi vào 10
2.1 Dạng bài rút gọn biểu thức, tính toán biểu thức, chứng minh đẳng thức
– Bài toán rút gọn biểu thức: Để rút gọn biểu thức A, ta thực hiện quy đồng mẫu thức (nếu có) rồi đưa bớt thừa số ra ngoài căn thức (nếu có), trục căn thức ở mẫu (nếu có). Thực hiện các phép tính lũy thừa, khai căn, nhân chia… rồi cộng trừ các số hạng đồng dạng để được biểu thức rút gọn.
– Bài toán tính giá trị biểu thức A mà không có điều kiện kèm theo đồng nghĩa với nó là bài toán rút gọn biểu thức A. Còn với bài toán tính giá trị biểu thức A(x) biết x = a ta thực hiện rút gọn biểu thức A(x) rồi sau đó thay x = a vào để tính toán.
– Bài toán chứng minh đẳng thức A = B:
+ Phương pháp 1: A = B
+ Phương pháp 2: A = A1 = A2 = … = B
+ Phương pháp 3: So sánh A = A1 = … = C và B = B1 = … = C => A = B
2.2 Dạng bài chứng minh bất đẳng thức
– Một số bất đẳng thức quan trọng:
+ Bất đẳng thức cosi:
Dấu “=” xảy ra khi và chỉ khi a1 = a2 = a3 = … = an.
+ Bất đẳng thức BunhiaCopxki:
Với mọi số a1 ; a2 ; a3 ;…; an ; b1; b2; b3;…;bn
Dấu “=” xảy ra khi và chỉ khi:
– Cách chứng minh:
+ Dựa vào đinh nghĩa: A > B
+ Biến đổi trực tiếp: A = A1 = A2 = … = M2 + B > 0 ( M 0)
+ Dùng tính chất bắc cầu: A > C và C > B => A > B
2.3 Dạng bài liên quan đến phương trình bậc hai
– Bài tập giải phương trình bậc hai ax2 + bx + c = 0 (a 0)
+ Phương pháp 1: Đưa về dạng phương trình tích
+ Phương pháp 2: Dùng kiến thức về căn bậc 2: x2 = a
+ Phương pháp 3: Dùng công thức nghiệm:
Công thức nghiệm Công thức nghiệm thu gọn
Nếu > 0: Phương trình có hai nghiệm phân biệt:
Nếu = 0: Phương trình có nghiệm kép:
Nếu < 0: Phương trình vô nghiệm.
với b = 2b’
Nếu ‘ > 0: Phương trình có hai nghiệm phân biệt:
Nếu ‘ = 0: Phương trình có nghiệm kép:
Nếu ‘ < 0: Phương trình vô nghiệm.
+ Phương pháp 4: Áp dụng định lí Viet: Nếu x1; x2 là nghiệm của phương trình bậc hai ax2 + bx + c = 0 (a 0) thì:
– Tìm điều kiện của tham số m để phương trình bậc hai ax2 + bx + c = 0 (a 0) có nghiệm:
+ Có hai khả năng để phương trình có nghiệm:
- Hoặc a = 0 ; b 0
- Hoặc a 0; 0 hoặc
=> Tập hợp các giá trị m là toàn bộ các giá trị m thỏa mãn 1 trong hai điều kiện trên.
– Tìm điều kiện của tham số m để phương trình bậc hai ax2 + bx + c = 0 (a 0) có nghiệm phân biệt:
+ Điều kiện là:
– Tìm điều kiện của tham số m để phương trình bậc hai ax2 + bx + c = 0 (a 0) có 1 nghiệm
+ Điều kiện là: hoặc
2.4 Dạng bài chứng minh hai góc bằng nhau, hai đoạn thẳng bằng nhau
– Cách chứng minh hai góc bằng nhau:
- Chứng minh hai góc cùng bằng góc thứ ba;
- Chứng minh hai góc bằng với hai góc bằng nhau khác;
- Chứng minh hai góc cùng phụ hoặc bù với góc thứ ba;
- Chứng minh hai góc cùng nhọn hoặc cùng tù có các cạnh đôi một song song hoặc vuông góc;
- Chứng minh hai góc so le trong, so le ngoài hoặc đồng vị;
- Chứng minh hai góc ở vị trí đối đỉnh nhau;
- Chứng minh hai góc của cùng một tam gaics cân hoặc đều;
- Chứng minh hai góc tương ứng của hai tam giác bằng nhau hoặc đồng dạng.
– Cách chứng minh hai đoạn thẳng bằng nhau:
- Chứng minh hai đoạn thẳng cùng bằng đoạn thẳng thứ ba;
- Chứng minh hai cạnh của một tam giác cân hoặc tam giác đều;
- Chứng minh hai cạnh tương tứng của hai tam giác bằng nhau;
- Chứng minh hai cạnh đối của hình bình hành, hình chữ nhật, hình thoi, hình vuông;
- Chứng minh hai cạnh bên của hình thang cân.
2.5 Dạng bài chứng minh hai đường thẳng song song, vuông góc
– Cách chứng minh hai đường thẳng song song
- Chứng minh hai đường thẳng cùng song song với đường thẳng thứ ba;
- Chứng minh hai đường thẳng cùng vuông góc với đường thẳng thứ ba;
- Chứng minh hai đường thẳng cùng tạo với cát tuyến hai góc bằng nhau ở vị trí so le trong, so le ngoài, góc đồng vị;
- Chứng minh hai đường thẳng là hai cạnh đối của hình bình hành, hình vuông, hình chữ nhật.
– Cách chứng minh hai đường thẳng vuông góc
- Chứng minh hai đường thẳng song song với đường thẳng vuông góc khác;
- Chứng minh chúng là chân đường cao trong một tam giác;
- Chứng minh chúng là phân giác của hai góc kề bù nhau.
2.6 Dạng bài chứng minh hai tam giác bằng nhau, hai tam giác đồng dạng
– Cách chứng minh hai tam giác thường bằng nhau: Dựa vào các trường hợp bằng nhau của tam giác là trường hợp góc-cạnh-góc; cạnh-góc-cạnh; cạnh-cạnh-cạnh.
– Cách chứng minh hai tam giác vuông bằng nhau: Dựa vào các trường hợp cạnh huyền – góc nhọn; cạnh huyền – cạnh góc vuông; cạnh góc vuông đôi một bằng nhau.
– Cách chứng minh hai tam giác thường đồng dạng:
- Có hai góc bằng nhau đôi một;
- Có một góc bằng nhau xen giữa hai cạnh tương ứng tỉ lệ;
- Có ba cạnh tương ứng tỉ lệ.
– Cách chứng minh hai tam giác vuông đồng dạng:
- Có một góc nhọn bằng nhau;
- Có hai cạnh góc vuông tương ứng tỉ lệ.
2.7 Dạng bài chứng minh tứ giác nội tiếp
– Dấu hiệu nhận biết tứ giác nội tiếp
- Tứ giác có tổng hai góc đối bằng 180o;
- Tứ giác có góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện;
- Tứ giác có 4 đỉnh cách đều một điểm;
- Tứ giác có hai đỉnh kề nhau cùng nhìn cạnh chứa hai đỉnh còn lại dưới một góc
2.8 Dạng bài chứng minh MT là tiếp tuyến của đường tròn (O;R)
– Cách chứng minh:
- Chứng minh OT MT tại T (O;R)
- Chứng minh khoảng cách từ tâm O đến đường thẳng MT bằng bán kính;
- Dùng góc nội tiếp.
3. Tóm tắt kiến thức chi tiết ôn thi toán vào 10
Dưới đây là tóm tắt chi tiết trọng tâm kiến thức và các dạng đề ôn thi vào 10 môn toán:
Trên đây là kiến thức ôn thi toán vào 10 trọng tâm các em cần ghi nhớ, ôn tập các dạng bài nhuần nhuyễn để có thể dễ dàng giải các câu hỏi trong đề thi toán vào 10. Việc ôn tập kiến thức toán 9 nên thực hành song song với việc luyện đề sẽ giúp các em nhanh chóng ghi nhớ công thức, tính chất toán học.
Để luyện thêm nhiều dạng đề thi toán vào 10, các em có thể tham khảo khóa học ôn thi vào 10 của nhà trường VUIHOC. Tại đây, các em không chỉ được học và ôn thi cùng các thầy cô có kinh nghiệm đến từ các trường chuyên nổi tiếng mà còn được tham gia các buổi thi thử được tổ chức bởi nhà trường VUIHOC, giúp đánh giá điểm số và năng lực của các em sau quá trình ôn luyện.
>> Mời bạn tham khảo thêm:
- 16 chuyên đề toán ôn thi vào 10 cần nhớ
- Tổng hợp đề thi thử toán vào 10 cùng đáp án chi tiết

