Toán hình lớp 12 là một phần quan trọng trong chương trình học và kỳ thi Đại học nên đòi hỏi học sinh cần phải nắm vững các công thức tính toán. Điều này không chỉ là cách học tốt toán hình không gian mà còn giúp học sinh dễ dàng giải quyết các bài toán hình học phức tạp. Để hỗ trợ các bạn học sinh chuẩn bị tốt nhất cho kỳ thi sắp tới, bài viết này của Trường Việt Anh sẽ tổng hợp đầy đủ các công thức toán hình 12, bao gồm các khối đa diện, khối nón, khối trụ và các phương pháp tính trong không gian tọa độ.
Tổng hợp công thức toán hình 12 khối đa diện
Khối đa diện là phần kiến thức trọng tâm trong chương trình công thức toán hình 12, bao gồm các hình chóp, lăng trụ và hình hộp chữ nhật. Dưới đây là những công thức toán hình 12 liên quan đến các khối đa diện thường gặp, giúp bạn dễ dàng áp dụng vào các bài toán thể tích và diện tích.
>>Xem thêm: Trọn bộ công thức tính thể tích hình khối đầy đủ nhất
Công thức toán hình 12 khối đa diện
Công thức toán 12 về cách tính thể tích khối chóp thường sẽ được áp dụng cho cả chóp tam giác và chóp tứ giác đều. Thể tích khối chóp được tính bằng một phần ba diện tích mặt đáy nhân với chiều cao. Công thức này chung cho các khối chóp có đáy là tam giác hoặc tứ giác.
Thể tích khối chóp: [V = frac{1}{3} S_{đáy} times h]
Trong đó:
- (S_{đáy}): Diện tích mặt đáy
- h: Chiều cao
Công thức toán hình 12 khối lăng trụ
Khối lăng trụ có hai đáy nằm trên hai mặt phẳng song song và các cạnh bên song song với nhau. Thể tích khối lăng trụ được tính bằng diện tích đáy nhân với chiều cao.
- Thể tích khối lăng trụ: V = S × h
Trong đó:
- S: Diện tích mặt đáy
- h: Chiều cao
Lưu ý, với lăng trụ đứng, chiều cao chính là độ dài cạnh bên. Ngoài ra, bạn có thể áp dụng các công thức toán 12 hình học để tính thể tích khối lăng trụ tam giác đều trong các bài toán liên quan.
Thể tích hình hộp chữ nhật lớp 12
Hình hộp chữ nhật là một dạng khối phổ biến với các cạnh đáy lần lượt là a, b và chiều cao c. Công thức tính thể tích hình hộp chữ nhật:
- Thể tích hình hộp chữ nhật: V = a × b × c
Trong đó:
- a, b, c: Các cạnh đáy và chiều cao của hình hộp (có cùng đơn vị)
Hình lập phương là một trường hợp đặc biệt của hình hộp chữ nhật khi a = b = c, và thể tích được tính bằng công thức V = a³.
Công thức toán hình 12 khối chóp cụt
Khối chóp cụt là phần nằm giữa mặt đáy và thiết diện cắt bởi mặt phẳng song song với đáy của hình chóp. Đây là một dạng khối thường gặp trong các bài toán công thức toán hình học 12:
Diện tích xung quanh hình chóp cụt
Diện tích xung quanh là diện tích của các mặt bên, không bao gồm hai mặt đáy. Công thức tính diện tích xung quanh của hình chóp cụt được tính bằng tổng diện tích các mặt bên, thường là hình thang.
Công thức:
[S_{xq} = n cdot S_{mặt;bên}]
[Rightarrow S_{xq} = n cdot frac{1}{2}(a + b) cdot h]
Trong đó:
- (S_{xq}): Diện tích xung quanh.
- n: Số lượng mặt bên.
- a, b: Chiều dài cạnh của 2 đáy trên và dưới của hình chóp cụt.
- h: Chiều cao mặt bên.
Công thức tính diện tích toàn phần
Diện tích toàn phần của hình chóp cụt (S_{xq}) được tính bằng tổng diện tích xung quanh và diện tích hai đáy của hình chóp cụt.
[S_{tp} = S_{xq} + S_{đáy;lớn} + S_{đáy;nhỏ}]
Trong đó:
- (S_{xq}): Diện tích xung quanh.
- (S_{đáy}) lớn: Diện tích đáy lớn.
- (S_{đáy}) nhỏ: Diện tích đáy nhỏ.
Thể tích hình chóp cụt được tính bằng công thức
Thể tích hình chóp cụt (V) được tính theo công thức:
[V = frac{1}{3} cdot h cdot left( S + S’ + sqrt{S cdot S’} right)]
Trong đó:
- h: Chiều cao của hình chóp cụt (khoảng cách giữa hai mặt đáy).
- S: Diện tích mặt đáy lớn.
- S′: Diện tích mặt đáy nhỏ.
Công thức toán hình 12 hình nón
Khối nón là một trong những hình học không gian quen thuộc trong chương trình công thức toán hình 12. Hình nón có không gian ba chiều với phần đỉnh nhọn và mặt đáy phẳng là hình tròn. Để dễ hình dung, các em có thể liên tưởng đến các vật dụng xung quanh như chiếc nón lá hay mũ sinh nhật, đều có hình dạng tương tự hình nón.
Công thức diện tích xung quanh hình nón
Diện tích xung quanh Sxq của hình nón được tính bằng công thức:
[S_{xq} = π.r.l]
Trong đó:
- π: Hằng số Pi (≈ 3,14).
- r: Bán kính mặt đáy hình nón.
- l: Đường sinh của hình nón.
Công thức này giúp tính diện tích bao quanh bề mặt cong của hình nón, không bao gồm mặt đáy.
Công thức toán hình 12 về tính toàn phần hình nón
Diện tích toàn phần (S_{xq}) của hình nón bao gồm diện tích xung quanh cộng với diện tích mặt đáy, được tính theo công thức:
[S_{tp} = S_{xq} + S_{đ} = pi r l + pi r^2]
Trong đó, (S_{d}) là diện tích mặt đáy của hình nón, được tính bằng công thức diện tích hình tròn:
[S_{d} = pi r^2]
Công thức tính thể tích khối nón
Thể tích (V) của khối nón được tính bằng công thức:
[V = frac{1}{3} cdot pi r^2 cdot h]
Trong đó:
- π: Hằng số Pi (≈ 3,14).
- r: Bán kính mặt đáy hình nón.
- h: Chiều cao của hình nón (khoảng cách từ đỉnh đến tâm của mặt đáy).
Nhờ việc nắm vững các công thức hình học toán 12, đặc biệt là công thức liên quan đến khối nón, các em sẽ dễ dàng giải quyết các bài toán về tính diện tích và thể tích trong đề thi.
Một số công thức toán hình 12 về tính mặt nón
Khi làm bài tập toán hình nón, việc tính thể tích của khối nón là rất quan trọng. Dưới đây là những công thức chi tiết giúp bạn tính diện tích và thể tích của hình nón chính xác:
[V = frac{1}{3} cdot pi r^2 cdot h]
[A_d = pi r^2]
[A_{xq} = pi r s]
[A = A_d + A_{xq}]
[A = pi r (r + s)]
[s = sqrt{r^2 + h^2}]
[d = 2r]
Trong đó:
- V: thể tích
- A: diện tích
- (A_{d}): diện tích đáy
- (A_{xq}): diện tích xung quanh
- r: bán kính
- d: đường kính
- h: đường cao s
Một số công thức khác:
- Đường cao: h=SO (hay còn gọi là trục của hình nón)
- Bán kính đáy: r=OA=OB=OM
- Đường sinh: l=SA=SB=SM
- Góc ở đỉnh: ASB
- Thiết diện qua trục SAB cân tại S
- Góc giữa mặt đáy và đường sinh: SAO=SBO=SMO
- Chu vi đáy: p= 2πr
- Diện tích đáy: [S_{đáy} = pi r^2]
Công thức toán hình lớp 12 về hình trụ
Hình trụ là một khối hình học đặc biệt, được giới hạn bởi hai mặt trụ có đường kính bằng nhau và có bán kính giống nhau. Trong công thức toán hình lớp 12, hình trụ xuất hiện khá thường xuyên và được ứng dụng rộng rãi trong nhiều bài toán từ đơn giản đến phức tạp. Dưới đây là những công thức quan trọng giúp bạn tính toán các thông số của hình trụ một cách nhanh chóng và chuẩn xác:
- Công thức tính thể tích khối trụ:
Thể tích của khối trụ sẽ bằng tích của diện tích đáy với chiều cao. Đây là công thức toán hình 12 cơ bản và thường xuyên xuất hiện trong các bài toán hình học mà học sinh cần ghi nhớ:
[V = pi r^2 h]
Trong đó:
- r: Bán kính của hình trụ,
- h: Chiều cao của hình trụ,
- π ≈ 3.14
- Diện tích xung quanh khối trụ:
Diện tích xung quanh của khối trụ là diện tích của mặt bên của hình trụ, được tính bằng tích của chu vi đáy và chiều cao.
[S_{xq} = 2π.r.h]
Trong đó:
- r: Bán kính của hình trụ
- h: Chiều cao nối từ đáy cho tới đỉnh của hình trụ.
- Công thức tính diện tích toàn phần
Diện tích toàn phần của khối trụ bao gồm diện tích xung quanh cộng với diện tích của hai đáy. Đây là công thức quan trọng thường được áp dụng khi muốn tính toàn bộ diện tích của khối trụ:
[S_{tp} = S_{xq} + 2S_{đáy} = 2pi r h + 2pi r^2]
Trong đó:
- (S_{xq}): Diện tích xung quanh
- (S_{đáy}): Diện tích đáy của hình trụ.
- Một số công thức hình trụ khác:
- Diện tích đáy:
[S_{đáy} = pi r^2]
-
- Chu vi đáy:
[p = 2πr]
Những công thức tính mặt cầu toán hình lớp 12
Mặt cầu là một khối hình học quan trọng trong hình học không gian, được xác định bởi tập hợp tất cả các điểm trong không gian có khoảng cách từ một điểm cố định (gọi là tâm) với một bán kính nhất định. Dưới đây là các công thức toán hình lớp 12 liên quan đến mặt cầu, giúp bạn tính toán diện tích và thể tích của khối cầu một cách chính xác.
- Thể tích khối cầu:
Công thức này tính thể tích của khối cầu, cho biết không gian mà khối cầu chiếm giữ trong không gian ba chiều. Đây là một trong những công thức tính toán hình cơ bản và rất quan trọng trong hình học lớp 12:
[V = frac{4}{3} pi r^3]
Trong đó: r: Bán kính của khối cầu..
- Diện tích mặt cầu:
Diện tích mặt cầu cho biết diện tích bề mặt của khối cầu. Công thức này giúp bạn tính diện tích của mặt cầu, từ đó giải quyết các bài toán liên quan đến khối cầu trong không gian ba chiều:
[S = 4pi R^2]
Trong đó: R: Bán kính của mặt cầu.
Những công thức trên là cơ sở để tính toán các thông số của mặt cầu và khối cầu, giúp bạn giải quyết các bài toán hình học liên quan trong chương trình học toán lớp 12.
Công thức toán hình 12 tọa độ trong không gian
Trong hình học không gian, việc sử dụng hệ tọa độ và các công thức liên quan là rất quan trọng để giải quyết các bài toán về tọa độ, vectơ, và các phương trình của các hình khối. Dưới đây là các công thức toán hình lớp 12 liên quan đến tọa độ trong không gian, giúp bạn hiểu và áp dụng các khái niệm này một cách hiệu quả.
Công thức tính hệ tọa độ Oxyz
Trong không gian với hệ tọa độ Oxyz, chúng ta có ba trục tọa độ vuông góc với nhau: trục hoành Ox, trục tung Oy, và trục cao Oz, với gốc tọa độ là điểm O. Mỗi mặt phẳng tọa độ (Oxy, Oyz, Ozx) chia không gian thành tám phần, gọi là các octant. Các vectơ đơn vị có ký hiệu toán học là ( bar{i}, bar{j}, bar{k} ), tương ứng với các hướng của trục Ox, Oy, và Oz. Trong hệ tọa độ này, các công thức vector cơ bản bao gồm:
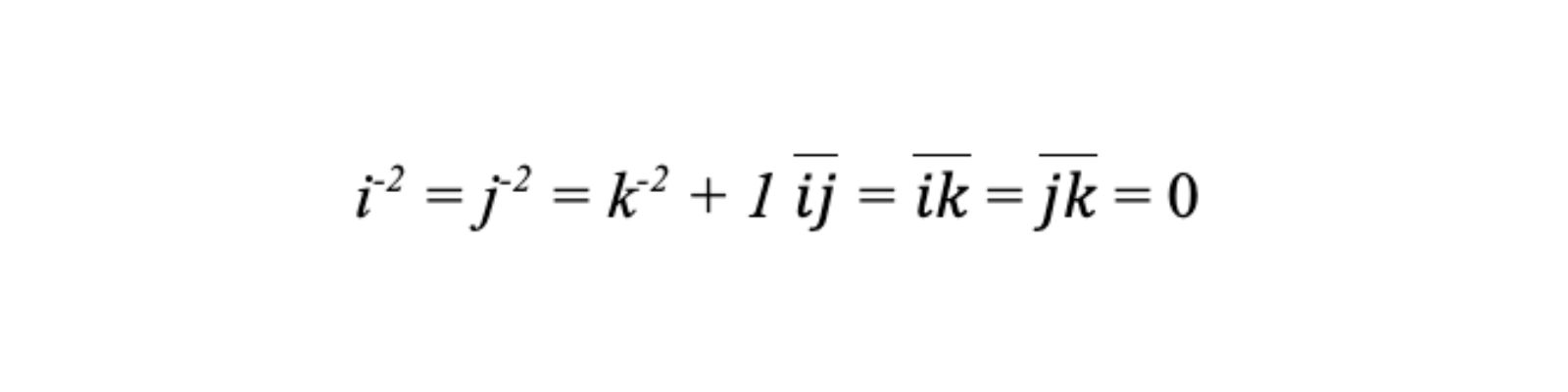
Công thức tính Vectơ
Vectơ trong không gian ba chiều được biểu diễn thông qua ba thành phần tọa độ x, y, z tương ứng với các trục tọa độ. Vectơ ( bar{ui} ) = (x, y, z) có thể được viết lại dưới dạng các vectơ đơn vị:
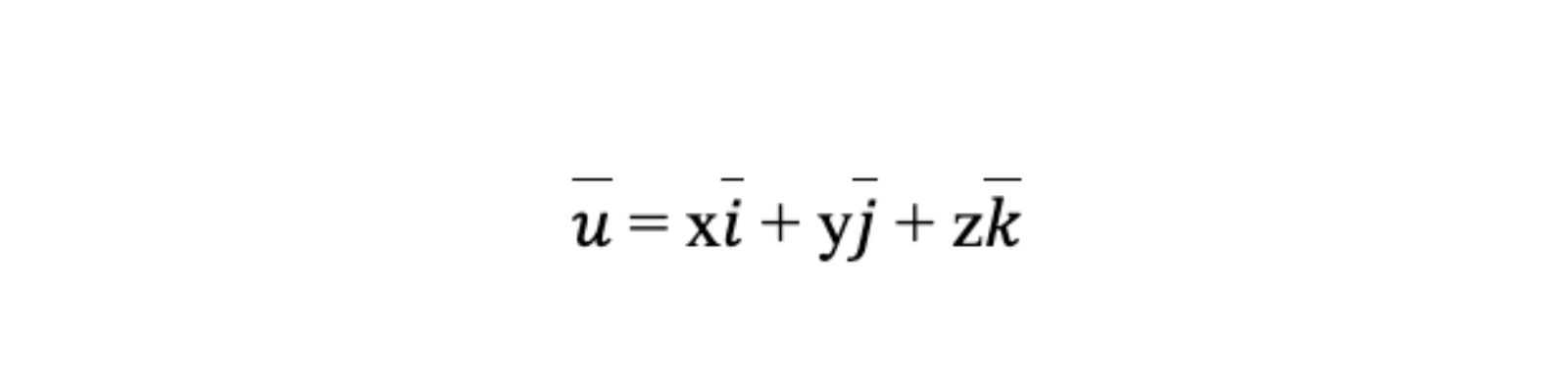
Với dạng công thức toán hình 12 nãy sẽ giúp học sinh dễ dàng biểu diễn vị trí và độ lớn của vectơ trong hệ tọa độ ba chiều, điều này cũng rất quan trọng trong việc giải các bài toán hình học không gian.
Công thức của tích có hướng của 2 vectơ
Tích có hướng của hai vectơ ( bar{u} ) = (a, b, c) và ( bar{u} ) = (a’, b’, c’) là một vectơ mới, được ký hiệu là [u, v]. Công thức tính tích có hướng như sau:
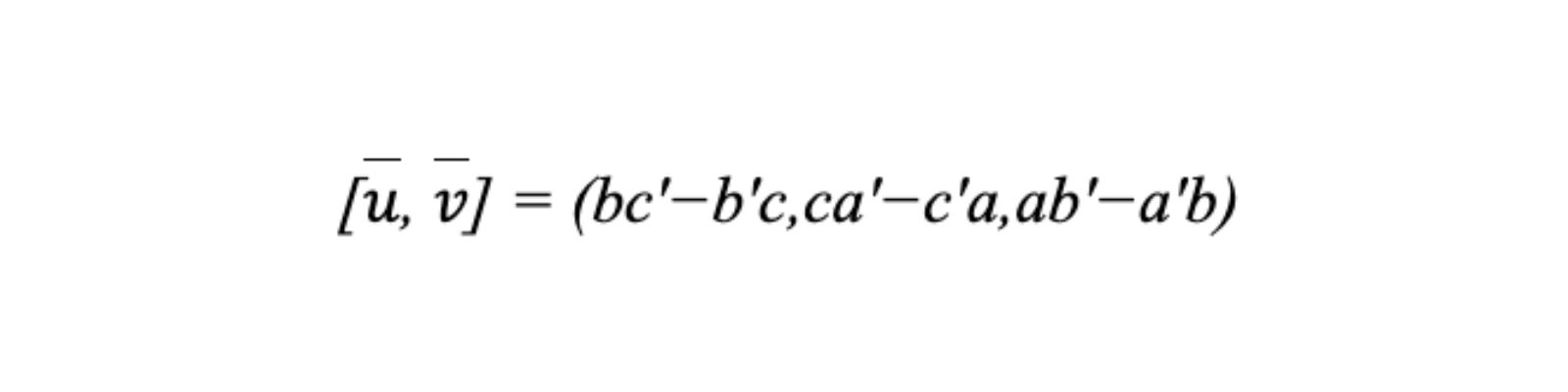
Tích có hướng của hai vectơ có các tính chất quan trọng, bao gồm:
- Tích có hướng luôn vuông góc với cả hai vectơ ( bar{u} ) và ( bar{v} )
- Độ lớn của tích có hướng được tính bằng công thức:
[ |[bar{u}, bar{v}]| = |bar{u}| cdot |bar{v}| cdot sin(bar{u}, bar{v}) ]
- Nếu ( [bar{u}, bar{v}] ) = ( bar{0} ), thì ( bar{u} ) và ( bar{v} ) cùng phương.
Công thức toán hình 12 về cách tính tọa độ điểm
Một điểm M trong không gian ba chiều có tọa độ (x,y,z). Vị trí của điểm M được xác định bởi vectơ ( bar{OM} ) nối từ gốc tọa độ O đến M, và điều này được biểu diễn như sau:
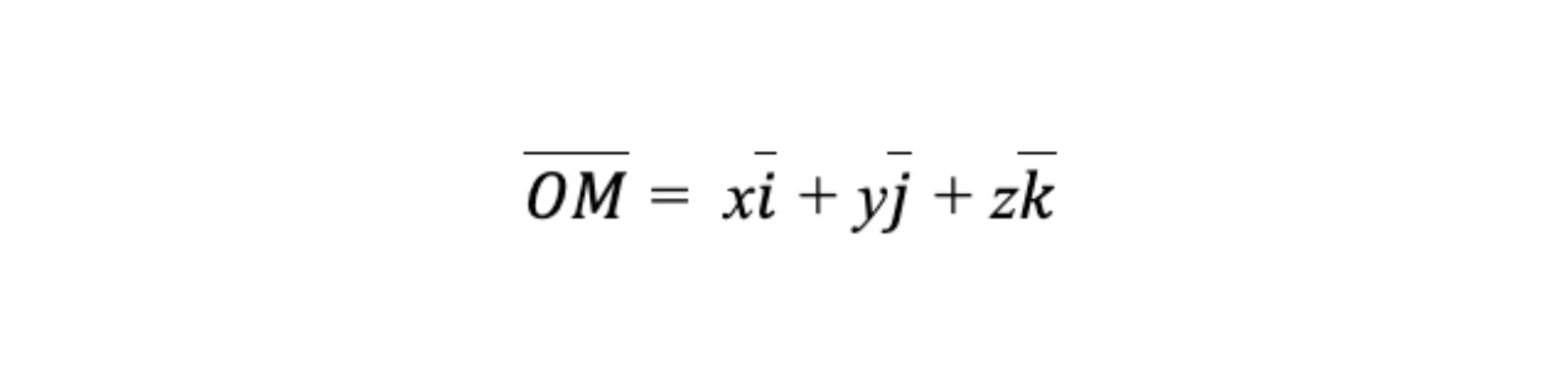
Phương trình mặt cầu, đường thẳng, mặt phẳng
Trong không gian Oxyz, một đường thẳng có thể được biểu diễn qua nhiều dạng phương trình khác nhau, bao gồm:
a) Phương trình mặt cầu
Phương trình mặt cầu biểu diễn tập hợp các điểm M (x, y, z) trong không gian có khoảng cách không đổi (bán kính R) đến một điểm cố định I = (a, b, c) gọi là tâm mặt cầu.
- Dạng 1: Phương trình mặt cầu có tâm I = (a, b, c) và bán kính R:
[ (x – a)^2 + (y – b)^2 + (z – c)^2 = R^2 ]
- Dạng 2: Phương trình mặt cầu dạng mở rộng:
[ x^2 + y^2 + z^2 – 2ax – 2by – 2cz + d = 0 ]
Với điều kiện [ a^2 + b^2 + c^2 – d > 0 ]
Tâm mặt cầu là I (a, b, c) và bán kính [R = sqrt{a^2 + b^2 + c^2 – d}].
b) Phương trình đường thẳng trong không gian
- Vectơ chỉ phương của đường thẳng:
Cho đường thẳng d, nếu vectơ ( bar{a} neq 0 ) có giá song song hoặc trùng với đường thẳng d, thì ( bar{a} ) được gọi là vectơ chỉ phương (VTCP) của d. Vectơ này thường có dạng: 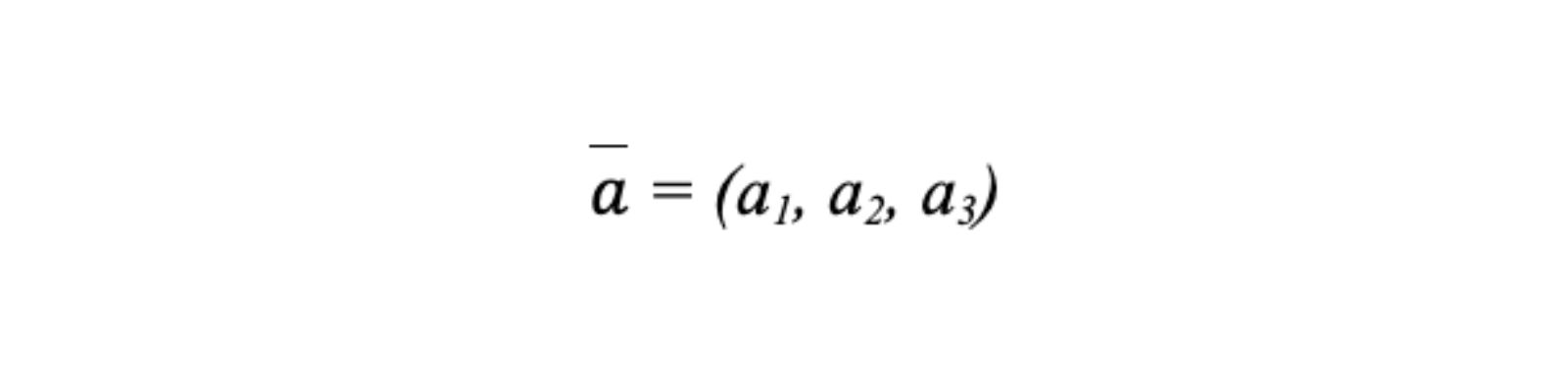
Ví dụ, vectơ chỉ phương của các trục tọa độ là:
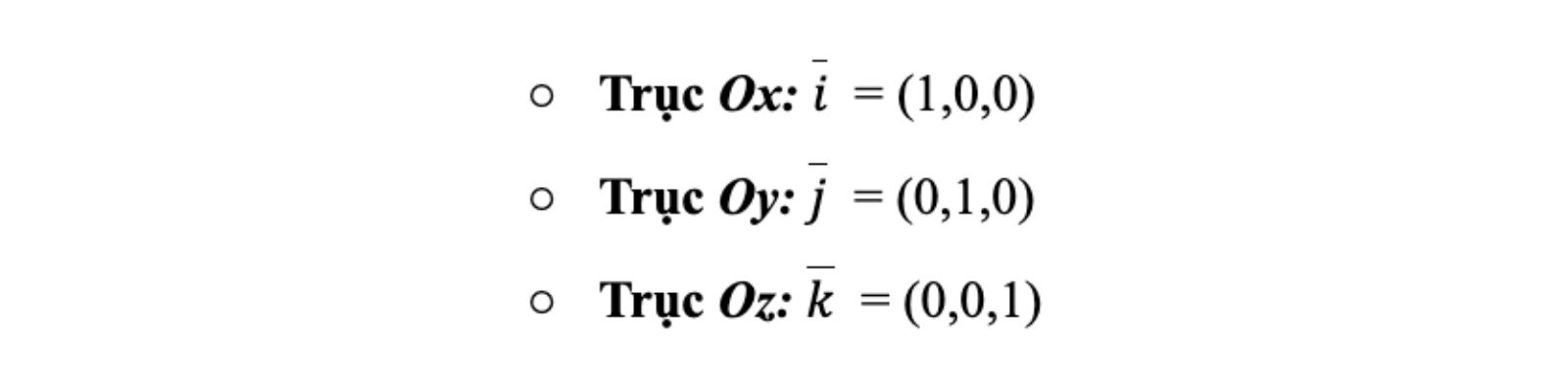
- Phương trình tham số của đường thẳng:
Đường thẳng đi qua điểm (M_0)((x_0), (y_0), (z_0)) và có VTCP ( bar{a} ) = ((a_1), (a_2), (a_3)) sẽ có phương trình tham số:
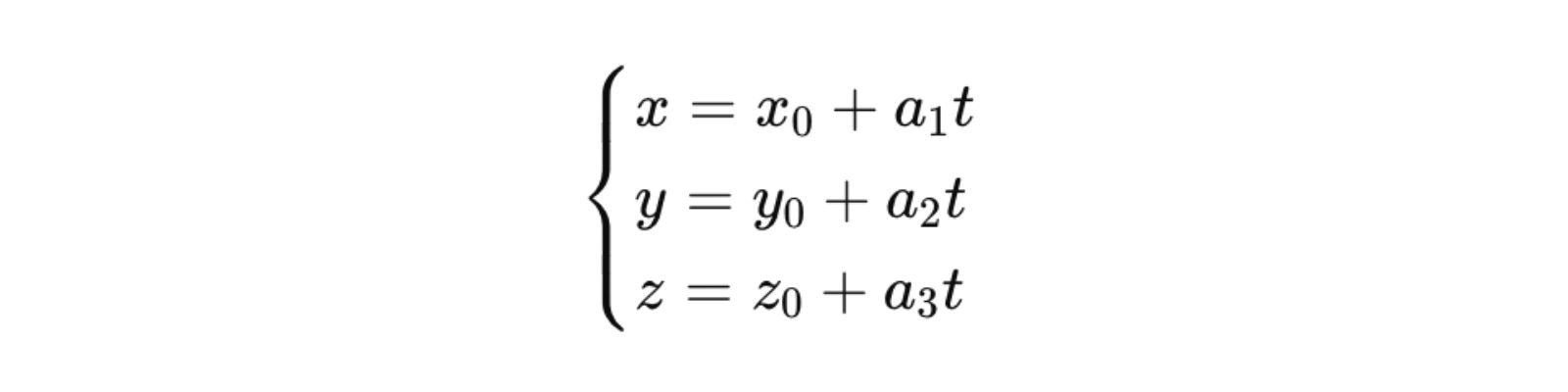
- Phương trình chính tắc của đường thẳng:
Phương trình chính tắc của đường thẳng Δ đi qua điểm (M_0)((x_0), (y_0), (z_0)) và có VTCP ( bar{a} ) = ((a_1), (a_2), (a_3)) là:
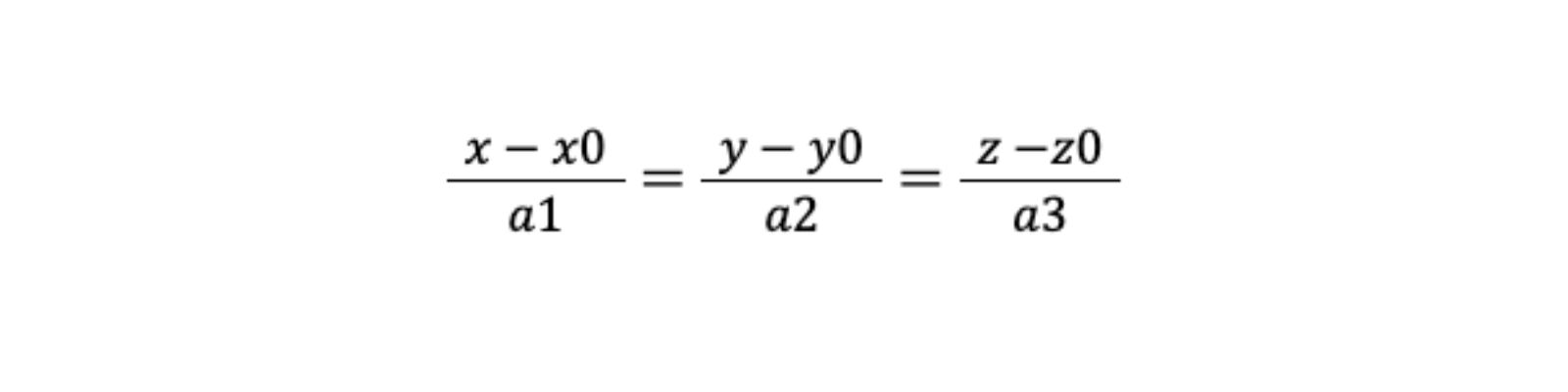
c) Phương trình mặt phẳng:
- Phương trình tổng quát:
Mặt phẳng a có phương trình tổng quát:
Ax + By + Cz + D = 0
Vectơ pháp tuyến của mặt phẳng là ( bar{a} ) = (A, B, C) với ( A^2 + B^2 + C neq 0 ).
- Phương trình đoạn chắn:
Mặt phẳng đi qua các điểm A (a, 0, 0), B (0, b, 0), C (0, 0, c) có phương trình đoạn chắn:
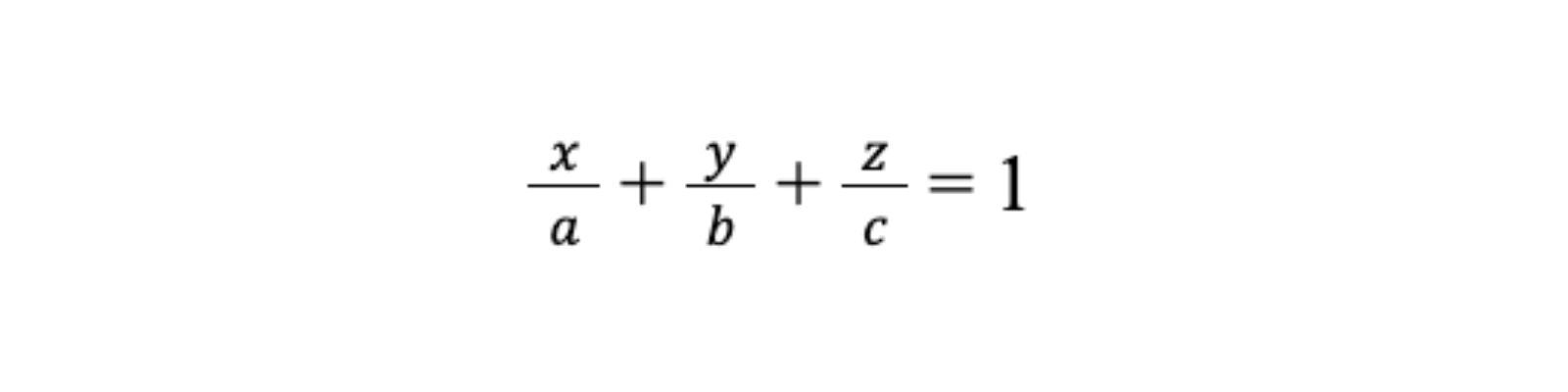
- Góc giữa hai mặt phẳng:
Cho hai mặt phẳng a: Ax + By + Cz + D = 0 và b: A’x + B’y + C’z + D’ = 0, góc giữa hai mặt phẳng được tính bằng công thức:
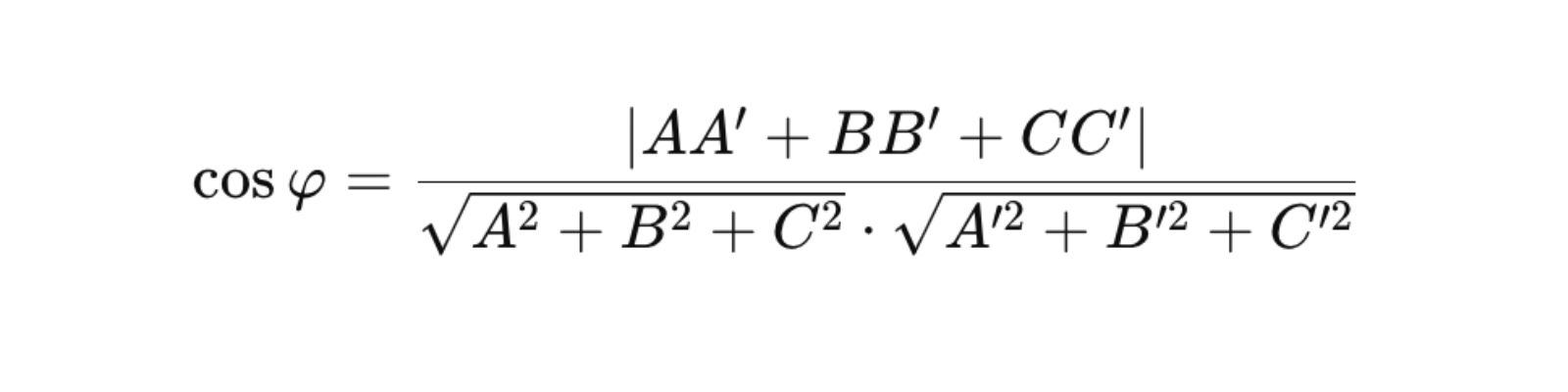
- Khoảng cách từ một điểm đến mặt phẳng:
Khoảng cách từ điểm (M_0)((x_0), (y_0), (z_0)) đến mặt phẳng a: Ax + By + Cz + D = 0 được tính bằng công thức:
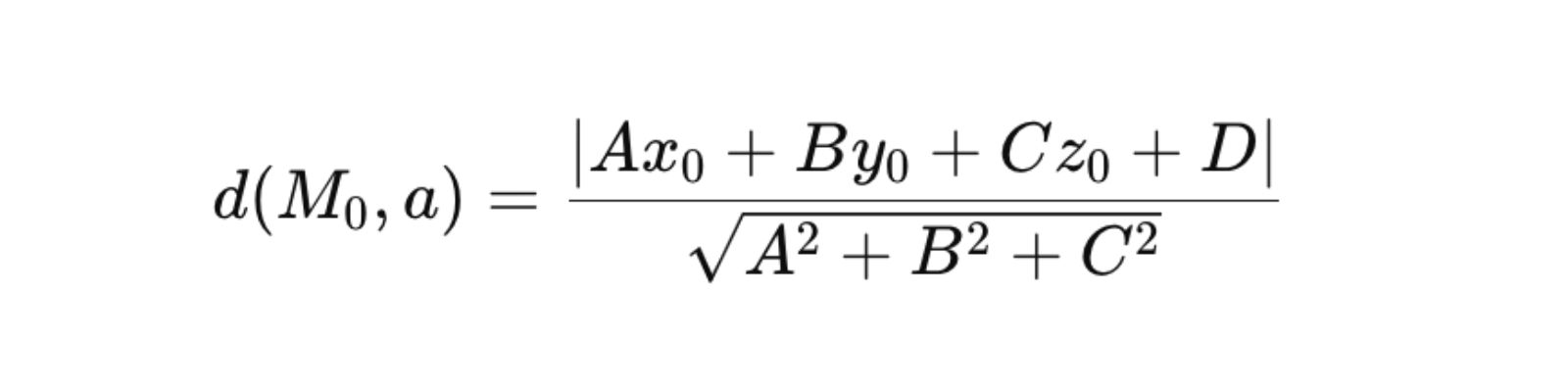
Hiểu và nắm vững những công thức toán hình 12 không chỉ là cách học giỏi toán phần hình học không gian mà còn giúp bạn giải quyết nhanh chóng các bài tập trong sách giáo khoa. Đồng thời, còn giúp rèn luyện tư duy logic, khả năng phân tích và giải quyết vấn đề. Đây là những kỹ năng quan trọng, cần thiết cho việc học tập và phát triển sau này.
Nếu bạn đang tìm kiếm một Trường Quốc Tế với môi trường học tập năng động, sáng tạo, nơi bạn có thể phát triển toàn diện cả về kiến thức và kỹ năng, hãy đến với Trường Việt Anh. Với đội ngũ giáo viên tận tâm, giàu kinh nghiệm và chương trình học tập hiện đại, Việt Anh sẽ là nơi chắp cánh cho những ước mơ của bạn.
Mọi thông tin chi tiết về chương trình đào tạo và học phí trường Quốc Tế tại Trường Việt Anh, vui lòng liên hệ theo một trong những phương thức sau:
- Địa chỉ:
- Cơ sở Gò Vấp: 160/72 Phan Huy Ích, phường An Hội Tây, Tp.HCM.
- Cơ sở Phú Nhuận: 269A Nguyễn Trọng Tuyển, phường Phú Nhuận, Tp.HCM.
- Cơ sở Bình Tân: 951/7 Tỉnh lộ 10, phường Bình Tân, Tp.HCM.
- Hotline: 091 696 1409
- Zalo: 0901849306
- Website: www.truongvietanh.com

