Học công thức tính Vectơ là một phần quan trọng của toán học và được ứng dụng rộng rãi trong đời sống hàng ngày, các bài toán về Vectơ sẽ giúp bạn rèn luyện kỹ năng phân tích và giải quyết vấn đề phức tạp. Hãy cùng Trường Việt Anh tìm hiểu về công thức Vectơ lớp 10 và các bài tập ứng dụng qua bài viết.
Lý thuyết tổng hợp và các công thức Vectơ lớp 10
Lý thuyết tổng hợp công thức Vectơ là một phần quan trọng trong toán học lớp 10, giúp chúng ta hiểu rõ hơn về cách hoạt động của Vectơ và cách chúng tương tác với nhau. Việc hiểu sâu về lý thuyết Vectơ cũng giúp bạn phát triển kỹ năng tư duy logic, tư duy không gian và khả năng giải toán nâng cao.
Tham khảo: Cách học Toán lớp 10 hiệu quả nhanh chóng
Các định nghĩa
Hiểu rõ các khái niệm cơ bản Vectơ lớp 10 và các tính chất của chúng giúp chúng ta giải quyết nhiều bài toán từ đơn giản đến phức tạp trong toán học và các lĩnh vực ứng dụng khác.
Khái niệm Vectơ
Vectơ được biểu diễn bằng một đoạn thẳng có hướng, có điểm đầu và điểm cuối. Chúng được sử dụng để biểu diễn các đại lượng có cả độ lớn và hướng như lực, vận tốc, gia tốc.
Công thức:
- Một Vectơ 𝐀 trong không gian hai chiều có thể được biểu diễn như sau: A=(a1,a2)
- Trong không gian ba chiều: A=(a1,a2,a3)
Công thức vectơ cùng phương
Hai Vectơ được gọi là cùng phương nếu chúng có giá song song hoặc trùng nhau. Hai Vectơ này có thể cùng nằm trên một đường thẳng hoặc trên các đường thẳng song song. Vectơ cùng phương không nhất thiết phải có cùng hướng hoặc độ lớn, thường xuất hiện trong các bài toán công thức Vectơ chỉ phương.
Điều kiện Vectơ A=(a1,a2,a3) và B=(b1,b2,b3) cùng phương nếu tồn tại số k sao cho: B=kA. Nghĩa là: b1=ka1, b2=ka2, b3=ka3.
Vectơ cùng hướng
Chỉ hai Vectơ vừa có giá song song vừa cùng chiều. Chúng sẽ cùng một hướng nhất định và độ lớn có thể khác nhau. Vectơ cùng hướng là một khái niệm quan trọng trong bài tập công thức tính độ dài Vectơ trong không gian.
Điều kiện Vectơ A và B cùng hướng nếu chúng thỏa mãn điều kiện cùng phương và k phải là số dương: B=kA, k>0
Hai Vectơ bằng nhau
Hai Vectơ được coi là bằng nhau nếu chúng có cùng độ lớn và cùng hướng. Nói cách khác, nếu bạn di chuyển một Vectơ mà không thay đổi độ dài hay hướng của nó thì hai Vectơ đó bằng nhau. Khái niệm này thường được sử dụng để so sánh các đại lượng vật lý trong không gian.
Điều kiện Vectơ A=(a1,a2,a3) và B=(b1,b2,b3) bằng nhau nếu: a1=b1, a2=b2, a3=b3.
Vectơ – không
Đây là khái niệm quan trọng trong công thức tính tọa độ Vectơ, vì nó là Vectơ trung tính trong phép cộng Vectơ. Vectơ – không sẽ không thay đổi khi cộng với bất kỳ Vectơ nào khác. Công thức Vectơ không được ký hiệu Toán học là 0 và trong không gian ba chiều là 0=(0,0,0).
Tổng và hiệu của hai Vectơ
Tổng và hiệu của hai Vectơ là các phép toán cơ bản trong toán học Vectơ để diễn đạt sự kết hợp và khác biệt giữa các Vectơ với nhau.
Tổng của hai Vectơ

Phép toán tìm tổng của hai Vectơ còn được gọi là phép cộng Vectơ.
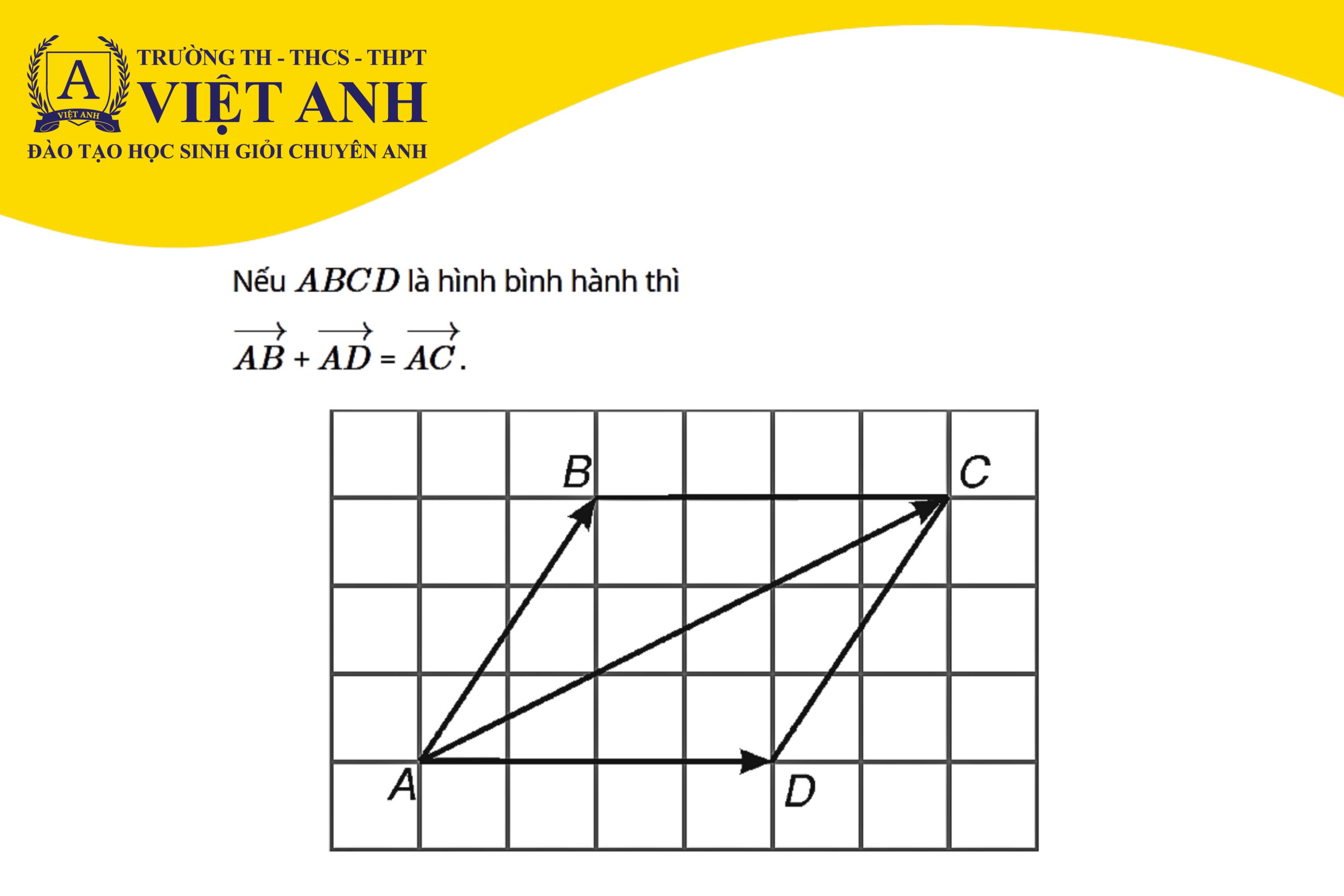
Tính chất của phép cộng các Vectơ

Hiệu của hai Vectơ
Đây là một Vectơ mới được tạo ra bằng cách trừ các thành phần tương ứng của hai Vectơ ban đầu. Nếu hai Vectơ được biểu diễn dưới dạng a và b thì hiệu của chúng là a−b. Trong không gian 2 chiều, nếu a=(a1,a2) và b=(b1,b2), thì a−b=(a1−b1,a2−b2).
Vectơ đối

Định nghĩa hiệu của hai Vectơ

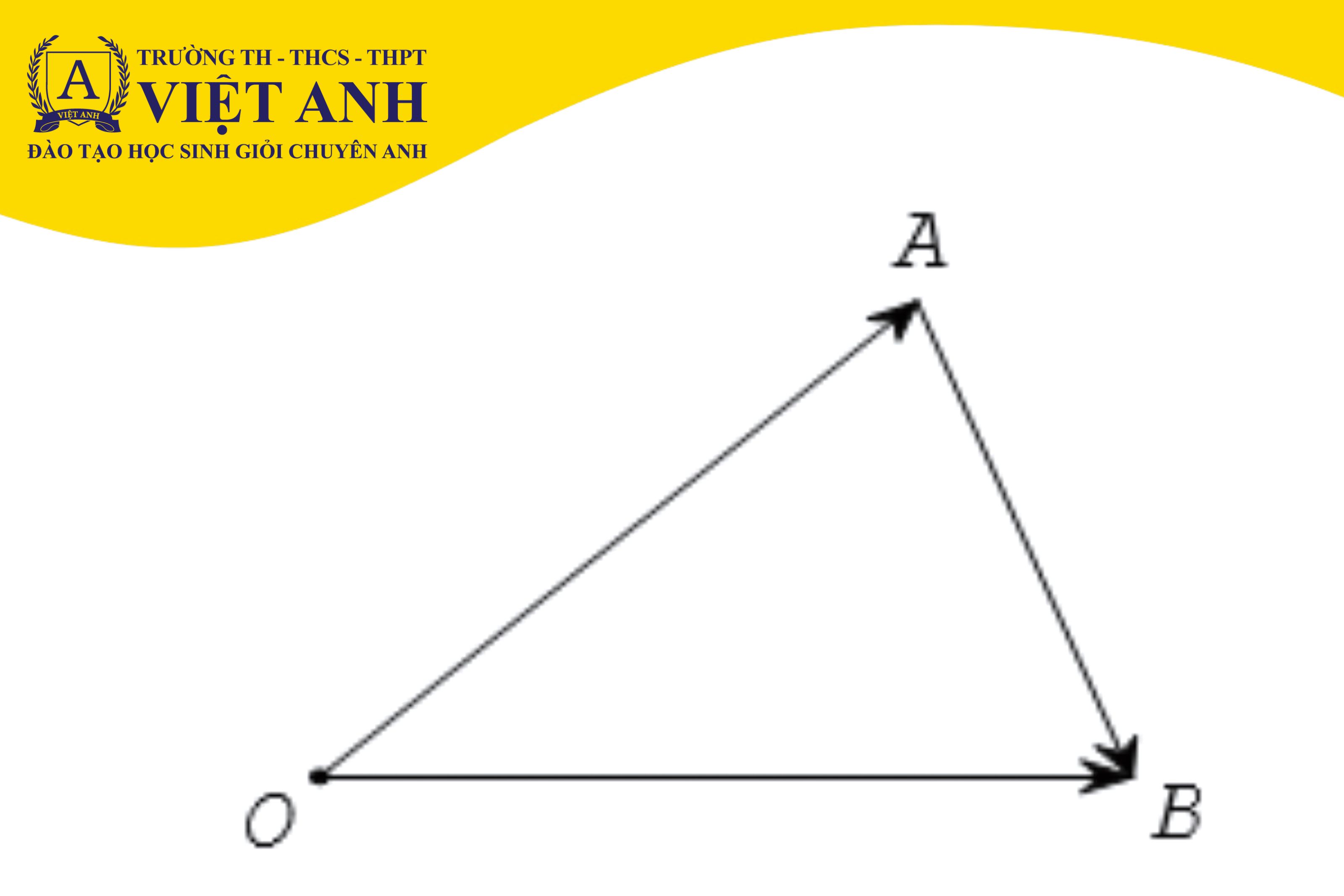
Định nghĩa này giúp chúng ta hiểu rằng hiệu Vectơ thực chất là thêm Vectơ đối của nó, làm cho việc tính toán công thức tính độ dài Vectơ ab trở nên đơn giản hơn.
Tích của Vectơ với một số
Định nghĩa
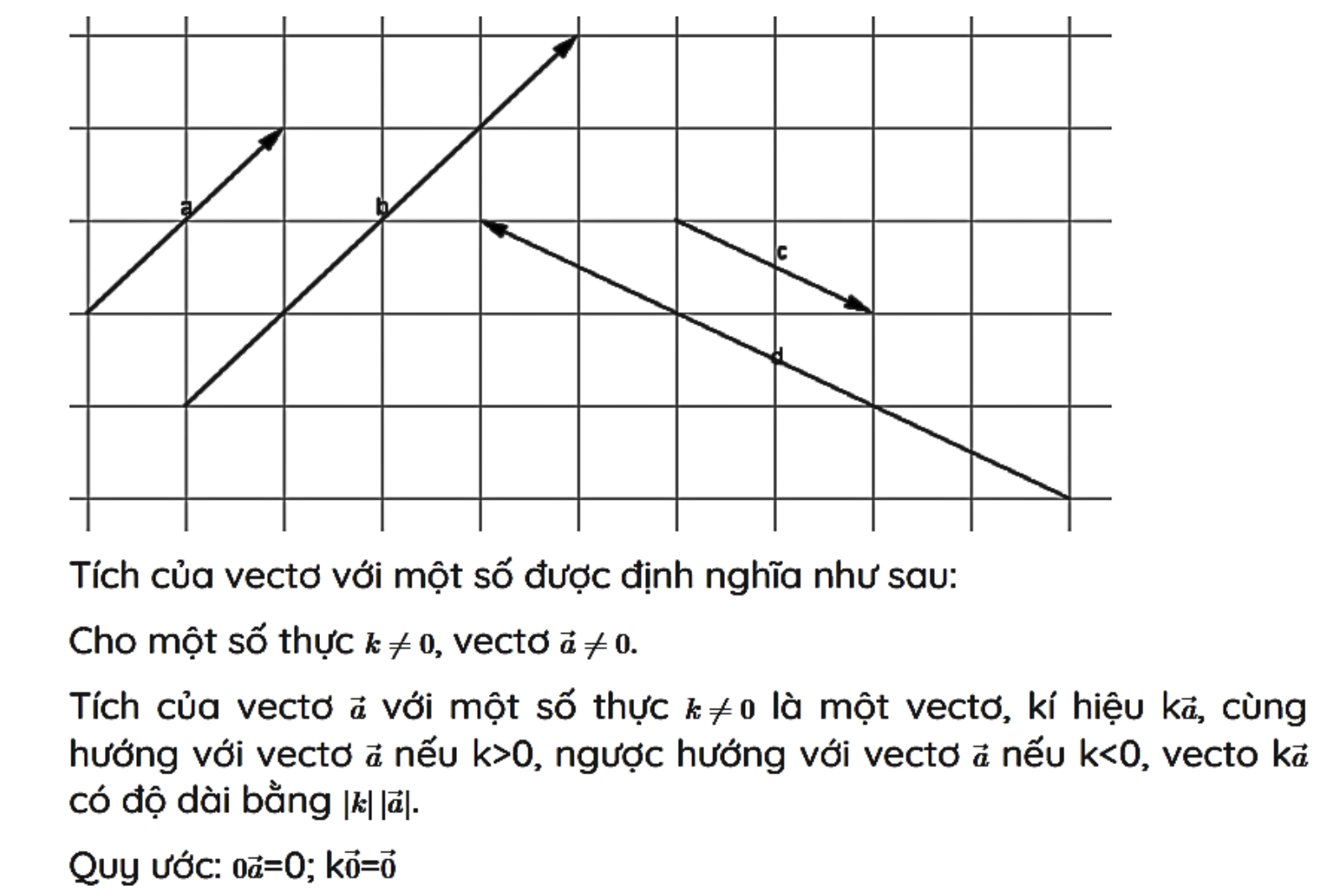
Tính chất

Trung điểm của đoạn thẳng và trọng tâm của tam giác
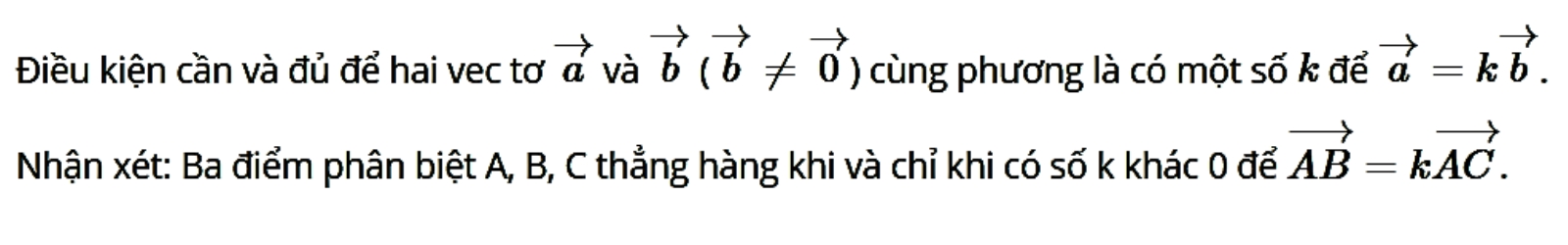
Điều kiện để hai Vectơ cùng phương

Phân tích một Vectơ theo hai Vectơ không cùng phương

Lý thuyết này thường được áp dụng trong các bài tập về công thức tích vô hướng của 2 Vectơ (hay công thức tính tích vô hướng của hai Vectơ).
Hệ trục tọa độ
Hệ trục tọa độ là một hệ thống xác định vị trí của các điểm trong không gian bằng cách sử dụng các trục số. Trong mặt phẳng, hệ trục tọa độ phổ biến nhất là Descartes gồm 2 trục vuông góc với nhau là trục hoành (trục x) và trục tung (trục y).
Trục và độ dài đại số trên trục
Trục trong hệ trục tọa độ là các đường thẳng được sử dụng làm cơ sở để xác định vị trí của các điểm. Độ dài đại số của một đoạn thẳng trên trục là khoảng cách từ một điểm gốc đến điểm đích trên cùng một trục, kèm theo dấu dương hoặc âm để chỉ phương.
Hệ trục tọa độ
Hệ trục tọa độ là một hệ thống các trục số thường vuông góc với nhau và được sử dụng để xác định vị trí của các điểm trong một không gian. Mỗi điểm trong không gian được xác định bởi một tập hợp các tọa độ, chẳng hạn như (x, y) trong hai chiều hoặc (x, y, z) trong ba chiều.
a. Định nghĩa: Trong hệ trục tọa độ, tọa độ là các số xác định vị trí của một điểm. Mỗi điểm trong không gian được mô tả bởi một tập hợp các số gọi là tọa độ, tương ứng với khoảng cách của điểm đó đến các trục tọa độ.
b. Tọa độ của Vectơ: Tọa độ của Vectơ là các giá trị xác định hướng và độ dài của Vectơ. Nếu a là một Vectơ trong mặt phẳng hai chiều và A(x1,y1) là điểm đầu và B(x2,y2) là điểm cuối của Vectơ thì tọa độ của Vectơ a là (x2−x1,y2−y1).
c. Tọa độ của một điểm: Đây là một cặp số (x, y) trong mặt phẳng hai chiều, hoặc một bộ ba số (x, y, z) trong không gian ba chiều. Các số này giúp xác định vị trí của điểm đó so với các trục tọa độ.
d. Liên hệ giữa tọa độ của điểm và tọa độ của Vectơ trong mặt phẳng: Trong mặt phẳng, tọa độ của một điểm có thể được sử dụng để xác định tọa độ của Vectơ.
Tọa độ của các Vectơ
Tọa độ của các Vectơ là các giá trị xác định hướng và độ dài của chúng. Với Vectơ a = (a1,a2) trong không gian hai chiều, a1 là thành phần x và a2 thành phần y. Trong không gian ba chiều, Vectơ a = (a1,a2,a3) có thêm thành phần z a3.
Tọa độ trung điểm của đoạn thẳng
Tọa độ trung điểm của đoạn thẳng nối hai điểm A(x_1, y_1) và B(x_2, y_2) là trung bình cộng của các tọa độ tương ứng của hai điểm đó. Công thức xác định tọa độ trung điểm M là [(x1+x2)/2,(y1+y2)/2]. Trung điểm này chia đoạn thẳng AB thành hai đoạn bằng nhau.
Tọa độ trọng tâm của tam giác
Tọa độ trọng tâm của tam giác là trung bình cộng của tọa độ các đỉnh của tam giác. Nếu tam giác có các đỉnh A(x_1, y_1), B(x_2, y_2), và C(x_3, y_3) thì tọa độ trọng tâm G là [(x1+x2+x3)/3,(y1+y2+y3)/3]. Trọng tâm là điểm giao của ba đường trung tuyến và chia mỗi đường trung tuyến theo tỷ lệ 2:1.
Các dạng bài tập về công thức Vectơ lớp 10
Xem và thực hành nhiều bài tập có lời giải về công thức Vectơ là một phương pháp học tập hiệu quả và cần thiết, đặc biệt trong lĩnh vực toán học. Dưới đây là các bài tập tổng hợp các công thức Vectơ và công thức tính góc giữa hai Vectơ có lời giải cho bạn tham khảo:
Bài tập Tìm tọa độ của một điểm, tọa độ Vectơ có đáp án
Câu hỏi: Cho ba điểm A(1,2,3), B(4,6,8) và C(7,9,11) trong không gian ba chiều. Tìm tọa độ của điểm D sao cho điểm D chia đoạn thẳng BC theo tỉ lệ 2:3. Sau đó, tính Vectơ AD.
Đáp án:
a. Tìm tọa độ của điểm D:
Điểm D chia đoạn thẳng BC theo tỉ lệ 2:3.
Áp dụng công thức điểm chia đoạn thẳng theo tỉ lệ với B(4,6,8), C(7,9,11), m=2, n=3 ta có:
D=(2×7+3×4/(2+3) , 2×9+3×6/(2+3) , 2×11+3×8/(2+3))
Trong đó:
xD=2×7+3×4/(2+3)=(14+12)/5=5.2
yD=2×9+3×6/(2+3)=(18+18)/5=36/5=7.2
zD=2×11+3×8/(2+3)=(22+24)/5=56/5=9.2
Vậy, tọa độ của điểm D là D(5.2,7.2,9.2)
b. Tính tọa độ của Vectơ AD:
Áp dụng công thức tọa độ của Vectơ với A(1,2,3), D(5.2,7.2,9.2) ta có: AD=(5.2−1,7.2−2,9.2−3)
Trong đó:
xAD=5.2−1=4.2
yAD=7.2−2=5.2
zAD=9.2−3=6.2
Vậy tọa độ của Vectơ AD là AD=(4.2,5.2,6.2)
Bài tập Tìm tổng của hai Vectơ và tổng của nhiều Vectơ có đáp án
Câu hỏi: Cho ba Vectơ u=(2,−1,3), v=(−4,5,1) và w=(0,−2,4). Hãy tìm:
– Tổng của hai Vectơ u+v.
– Tổng của ba Vectơ u+v+w.
Đáp án:
1. Tổng của hai Vectơ u+v sẽ được tính áp dụng theo công thức: a+b=(a1+b1,a2+b2,a3+b3), trong đó Vectơ a=(a1,a2,a3) và b=(b1,b2,b3)
Áp dụng công thức trên ta có: u+v=(2+(−4),−1+5,3+1)
Trong đó:
x(u+v)=2+(−4)=−2
y(u+v)=−1+5=4
z(u+v)=3+1=4
Vậy tổng của hai Vectơ u+v là u+v=(−2,4,4).
2. Tổng của hai Vectơ u+v sẽ được tính áp dụng theo công thức:
a+b+c=(a1+b1+c1,a2+b2+c2,a3+b3+c3), trong đó Vectơ a=(a1,a2,a3), b=(b1,b2,b3) và c=(c1,c2,c3)
Áp dụng công thức trên ta có: u+v+w=(2+(−4)+0,−1+5+(−2),3+1+4)
Trong đó:
x(u+v+w)=2+(−4)+0=−2
y(u+v+w)=−1+5+(−2)=2
z(u+v+w)=3+1+4=8
Vậy tổng của ba Vectơ u+v+w=(−2,2,8).
Bài tập tự luyện Tìm Vectơ đối và hiệu của hai Vectơ có đáp án
Câu hỏi: Cho hai Vectơ u=(3,−2,5) và v=(−1,4,−3). Tìm:
1. Vectơ đối của u.
2. Hiệu của hai Vectơ u−v.
Đáp án:
1. Vectơ đối của u sẽ được tính dựa theo công thức: −a=(−a1,−a2,−a3)
Áp dụng công thức trên ta có: −u=(−3,2,−5)
Vậy Vectơ đối của u là −u=(−3,2,−5)
2. Hiệu của hai Vectơ u−v sẽ được tính dựa theo công thức:
a−b=(a1−b1,a2−b2,a3−b3)
Áp dụng công thức trên ta có: u−v=(3−(−1),−2−4,5−(−3))
Suy ra:
x(u−v)=3−(−1)=3
y(u−v)=−2−4=−6
z(u−v)=5−(−3)=5+3=8
Vậy, hiệu của hai Vectơ u−v là u−v=(4,−6,8).
Bài tập tự luyện Phân tích một Vectơ qua hai Vectơ không cùng phương chọn lọc
Câu hỏi: Cho Vectơ v = (7,8) và hai Vectơ không cùng phương u = (1,2) và w = (3,1). Phân tích Vectơ v theo u và w; tức là tìm các số a và b sao cho v = au+bw.
Đáp án: Giả sử:
v = au+bw
(7,8) = a(1,2) + b(3,1)
Suy ra hệ phương trình:
7 = a+3b
8 = 2a+b => b = 8-2a
Thay vào phương trình thứ nhất:
7 = a+3(8−2a) => 7 = a+24−6a => 7 = 24−5a => 5a = 17 => a = 3.4
Thay a vào phương trình b = 8−2a => b = 8−2(3.4) => b = 1.2
Vậy a = 3.4 và b = 1.2, tức là: v = 3.4u+1.2w
Xem thêm: Cách giải phương trình bậc 2 đơn giản kèm theo File bài tập
Câu hỏi thường gặp về công thức Vectơ
1. Vectơ cùng phương là gì?
Là hai vectơ có giá song song hoặc trùng nhau.
2. Vectơ 0 là gì?
Là vectơ có độ dài bằng 0, điểm đầu trùng với điểm cuối.
3. Vectơ 0 bằng bao nhiêu?
Bằng 0
4. Tổng 2 vectơ bằng 0 khi nào?
Khi hai vectơ bằng nhau về độ dài, ngược hướng và cùng giá.
5. Giá của vectơ là gì?
Là đường thẳng đi qua điểm đầu và điểm cuối của vectơ.
6. Khi nào góc giữa hai vectơ bằng 0?
Là đường thẳng đi qua điểm đầu và điểm cuối của vectơ.
7. Hai vectơ vuông góc với nhau khi nào?
Khi góc giữa chúng bằng 90 độ.
Trường Việt Anh luôn tự hào là một trong những ngôi trường hàng đầu về chất lượng giáo dục và đào tạo học sinh toàn diện. Toán học được xem là một trong những môn học chủ chốt trong tất cả chương trình dạy. Nhà trường thường xuyên tổ chức các kỳ thi, cuộc thi toán và các buổi thảo luận chuyên đề để học sinh có cơ hội thực hành và phát triển kỹ năng tính toán, logic của mình.
Chúng tôi thiết kế chương trình giảng dạy toán học theo tiêu chuẩn quốc tế, kết hợp với những phương pháp giảng dạy tiên tiến và hiệu quả. Học sinh được tiếp cận với các kiến thức toán học từ cơ bản đến nâng cao. Đồng thời phát triển tư duy logic và khả năng giải quyết vấn đề nhanh chóng, là nền tảng vững chắc cho học sinh phát triển toàn diện và đột phá trong tương lai.
Như vậy, công thức Vectơ và những định nghĩa quan trọng liên quan đã được Trường Việt Anh gửi đến bạn đọc trong bài viết trên. Hy vọng bài viết sẽ mang lại thông tin hữu ích cho các bạn để hỗ trợ trong việc tiếp cận và giải toán Vectơ chính xác, dễ dàng. Đồng thời, nếu bạn đang tìm kiếm một trường tư thục giảng dạy chuyên nghiệp, chú trọng đào tạo Toán học thì liên hệ ngay với Trường Việt Anh qua hotline để được tư vấn chương trình học phù hợp nhất nhé.

