Đề bài
Câu 1 :
$M$ là trung điểm của đoạn thẳng $AB$ khi và chỉ khi:
-
A.
$MA = MB$
-
B.
\(AM = \dfrac{1}{2}AB\)
-
C.
\(MA + MB = AB\)
-
D.
$MA + MB = AB$ và $MA = MB$
Câu 2 :
Nếu ta có \(P\) là trung điểm của \(MN\) thì
-
A.
\(MP = NP = \dfrac{{MN}}{2}\)
-
B.
\(MP + NP = 2MN\)
-
C.
\(MP = NP = \dfrac{{MN}}{4}\)
-
D.
\(MP = NP = MN\)
Câu 3 :
Cho đoạn thẳng $AB$ dài $12cm$, $M$ là trung điểm của đoạn thẳng $AB.$ Khi đó, độ dài của đoạn thẳng $MA$ bằng
-
A.
$3cm$
-
B.
$15cm$
-
C.
$6cm$
-
D.
$20cm$
Câu 4 :
Cho $I$ là trung điểm của đoạn thẳng $MN.$ Biết $NI = 8cm$. Khi đó, độ dài của đoạn thẳng $MN$ bằng
-
A.
$4cm$
-
B.
$16cm$
-
C.
$21cm$
-
D.
$24cm$
Câu 5 :
Cho đoạn thẳng $AB.$Gọi $M$ và $N$ lần lượt là trung điểm của các đoạn thẳng $AB$ và $AM.$ Giả sử $AN = 1,5cm$. Đoạn thẳng $AB$ có độ dài là?
-
A.
$1,5cm$
-
B.
$3cm$
-
C.
$4,5cm$
-
D.
$6cm$
Câu 6 :
Cho đoạn thẳng $AB = 8cm$. Gọi $I$ và $K$ lần lượt là trung điểm của các đoạn thẳng $AB$ và $AI.$ Đoạn thẳng $IK$ có độ dài là?
-
A.
$8cm$
-
B.
$4cm$
-
C.
$2cm$
-
D.
$6cm$
Câu 7 :
Cho ba điểm $M,{\rm{ }}N,{\rm{ }}P$ thẳng hàng và điểm $N$ nằm giữa hai điểm $M$ và $P.$ Gọi $H,{\rm{ }}K$ lần lượt là trung điểm của các đoạn thẳng $MN,{\rm{ }}NP.$ Biết $MN = 5cm,NP = 9cm.$ Khi đó, độ dài của đoạn thẳng $HK$ bằng
-
A.
$4cm$
-
B.
$7cm$
-
C.
$14cm$
-
D.
$28cm$
Câu 8 :
Trên tia $Ox$ có các điểm $A,{\rm{ }}B$ sao cho $OA = 2cm;OB = 5cm.$ Gọi $M$ là trung điểm của đoạn thẳng $OB.$ Tính độ dài đoạn thẳng $AM.$
-
A.
$AM = 1,5cm.$
-
B.
$AM = 0,5cm.$
-
C.
$AM = 1cm.$
-
D.
$AM = 2cm.$
Câu 9 :
Trên đường thẳng $d$ vẽ đoạn thẳng $AB = 10cm.$ Lấy điểm $N$ nằm giữa hai điểm $A,{\rm{ }}B$ và $AN = 2cm.$ Gọi $M$ là trung điểm của đoạn thẳng $BN,$ gọi $P$ là trung điểm của đoạn thẳng $MN.$ So sánh \(MP\) và \(AN.\)
-
A.
$MP < AN.$
-
B.
$MP > AN.$
-
C.
$MP = AN.$
-
D.
Không đủ điều kiện so sánh
Trên tia $Ox$ lấy các điểm $M,{\rm{ }}N$ sao cho $OM = 2cm;ON = 3cm.$Trên tia đối của tia $NO$ lấy điểm $P$ sao cho $NP = 1cm.$
Tính độ dài các đoạn thẳng $MN$ và $MP.$
-
A.
$MN = 1cm;\,MP = 3cm$
-
B.
$MN = 2cm;\,MP = 3cm$
-
C.
$MN = 2cm;\,MP = 1cm$
-
D.
$MN = 1cm;\,MP = 2cm$
Hãy chọn câu đúng nhất
-
A.
$N$ là trung điểm của đoạn thẳng $MP.$
-
B.
$M$ là trung điểm của đoạn thẳng $OP.$
-
C.
$M$ là trung điểm của đoạn thẳng $NP. $
-
D.
Cả A, B đều đúng.
Lời giải và đáp án
Câu 1 :
$M$ là trung điểm của đoạn thẳng $AB$ khi và chỉ khi:
-
A.
$MA = MB$
-
B.
\(AM = \dfrac{1}{2}AB\)
-
C.
\(MA + MB = AB\)
-
D.
$MA + MB = AB$ và $MA = MB$
Đáp án : D
\(M\) là trung điểm của đoạn thẳng \(AB\)$ \Leftrightarrow \left\{ \begin{array}{l}AM + MB = AB\\{\rm{MA = MB}}\end{array} \right.$
Câu 2 :
Nếu ta có \(P\) là trung điểm của \(MN\) thì
-
A.
\(MP = NP = \dfrac{{MN}}{2}\)
-
B.
\(MP + NP = 2MN\)
-
C.
\(MP = NP = \dfrac{{MN}}{4}\)
-
D.
\(MP = NP = MN\)
Đáp án : A
Ta có \(P\) là trung điểm của \(MN\) thì \(MP = NP = \dfrac{{MN}}{2}\)
Câu 3 :
Cho đoạn thẳng $AB$ dài $12cm$, $M$ là trung điểm của đoạn thẳng $AB.$ Khi đó, độ dài của đoạn thẳng $MA$ bằng
-
A.
$3cm$
-
B.
$15cm$
-
C.
$6cm$
-
D.
$20cm$
Đáp án : C
Sử dụng kiến thức \(M\) là trung điểm của đoạn thẳng \(AB\) $ \Leftrightarrow {\rm{AM = BM = }}\dfrac{1}{2}AB$
Vì \(M\) là trung điểm của đoạn thẳng \(AB\) $ \Leftrightarrow {\rm{AM = }}\dfrac{1}{2}AB = \dfrac{1}{2}.12 = 6cm$
Vậy $AM = 6cm$.
Câu 4 :
Cho $I$ là trung điểm của đoạn thẳng $MN.$ Biết $NI = 8cm$. Khi đó, độ dài của đoạn thẳng $MN$ bằng
-
A.
$4cm$
-
B.
$16cm$
-
C.
$21cm$
-
D.
$24cm$
Đáp án : B
Sử dụng kiến thức \(M\) là trung điểm của đoạn thẳng \(AB\) $ \Leftrightarrow {\rm{AM = BM = }}\dfrac{1}{2}AB$
Vì $I$ là trung điểm của đoạn thẳng $MN$ nên $IM = IN = \dfrac{1}{2}MN$ hay $MN = 2.IN = 2.8 = 16cm$.
Câu 5 :
Cho đoạn thẳng $AB.$Gọi $M$ và $N$ lần lượt là trung điểm của các đoạn thẳng $AB$ và $AM.$ Giả sử $AN = 1,5cm$. Đoạn thẳng $AB$ có độ dài là?
-
A.
$1,5cm$
-
B.
$3cm$
-
C.
$4,5cm$
-
D.
$6cm$
Đáp án : D
Sử dụng kiến thức về trung điểm đoạn thẳng : “\(M\) là trung điểm của đoạn thẳng \(AB\) $ \Leftrightarrow {\rm{AM = BM = }}\dfrac{1}{2}AB$” để tính toán.
Vì $N$ là trung điểm đoạn $AM$ nên $AN = \dfrac{1}{2}AM$ hay $AM = 2AN = 2.1,5 = 3cm$
Lại có điểm $M$ là trung điểm đoạn thẳng $AB$ nên ta có $AM = \dfrac{1}{2}AB$ hay $AB = 2AM = 2.3 = 6cm$
Vậy $AB = 6cm$.
Câu 6 :
Cho đoạn thẳng $AB = 8cm$. Gọi $I$ và $K$ lần lượt là trung điểm của các đoạn thẳng $AB$ và $AI.$ Đoạn thẳng $IK$ có độ dài là?
-
A.
$8cm$
-
B.
$4cm$
-
C.
$2cm$
-
D.
$6cm$
Đáp án : C
Sử dụng kiến thức về trung điểm đoạn thẳng : “\(M\) là trung điểm của đoạn thẳng \(AB\) $ \Leftrightarrow {\rm{AM = BM = }}\dfrac{1}{2}AB$” để tính toán.
Vì điểm $I$ là trung điểm đoạn thẳng $AB$ nên $AI = \dfrac{1}{2}AB = \dfrac{1}{2}.8 = 4cm$
Vì điểm $K$ là trung điểm đoạn thẳng $AI$ nên $AK = \dfrac{1}{2}AI = \dfrac{1}{2}.4 = 2cm$
Vậy $AI = 2cm$.
Câu 7 :
Cho ba điểm $M,{\rm{ }}N,{\rm{ }}P$ thẳng hàng và điểm $N$ nằm giữa hai điểm $M$ và $P.$ Gọi $H,{\rm{ }}K$ lần lượt là trung điểm của các đoạn thẳng $MN,{\rm{ }}NP.$ Biết $MN = 5cm,NP = 9cm.$ Khi đó, độ dài của đoạn thẳng $HK$ bằng
-
A.
$4cm$
-
B.
$7cm$
-
C.
$14cm$
-
D.
$28cm$
Đáp án : B
Dựa vào tính chất trung điểm của đoạn thẳng.
“\(M\) là trung điểm của đoạn thẳng \(AB\) $ \Leftrightarrow {\rm{AM = BM = }}\dfrac{1}{2}AB$”

Vì $H$ là trung điểm của đoạn thẳng $MN$ nên $HN = \dfrac{1}{2}MN = \dfrac{1}{2} \cdot 5 = 2,5\,cm$.
Vì $K$ là trung điểm của đoạn thẳng $NP$ nên ${\rm{NK}} = \dfrac{1}{2}NP = \dfrac{1}{2} \cdot 9 = 4,5\,cm$.
Ta có $N$ nằm giữa hai điểm $M$ và $P$ nên $NM$ và $NP$ là hai tia đối nhau. (1)
Vì $H$ là trung điểm của $MN$ nên $H$ thuộc $NM$ (2)
Vì $K$ là trung điểm của $NP$ nên $K$ thuộc $NP$ (3)
Từ (1), (2) và (3) suy ra $N$ là điểm nằm giữa hai điểm $H$ và $K.$
\( \Rightarrow HN + NK = HK \Rightarrow 2,5 + 4,5 = HK\) \( \Rightarrow HK = 7\,cm.\)
Câu 8 :
Trên tia $Ox$ có các điểm $A,{\rm{ }}B$ sao cho $OA = 2cm;OB = 5cm.$ Gọi $M$ là trung điểm của đoạn thẳng $OB.$ Tính độ dài đoạn thẳng $AM.$
-
A.
$AM = 1,5cm.$
-
B.
$AM = 0,5cm.$
-
C.
$AM = 1cm.$
-
D.
$AM = 2cm.$
Đáp án : B
+ Sử dụng tính chất trung điểm của đoạn thẳng: “\(M\) là trung điểm của đoạn thẳng \(AB\) $ \Leftrightarrow {\rm{AM = BM = }}\dfrac{1}{2}AB$” để tính đoạn $OM$.
+ Sử dụng công thức cộng đoạn thẳng để tính đoạn $AM$.

Vì $M$ là trung điểm của đoạn thẳng $OB$ nên ta có $OM = \dfrac{1}{2}OB = \dfrac{1}{2}.5 = 2,5cm$
Vì $A$ và $M$ cùng thuộc tia $Ox$ mà $OA < OM\,\left( {2cm < 2,5cm} \right)$ nên điểm $A$ nằm giữa hai điểm $O$ và $M$.
Do đó $OA + AM = OM$ $ \Rightarrow AM = OM - OA = 2,5 - 2 = 0,5cm$
Vậy $AM = 0,5cm.$
Câu 9 :
Trên đường thẳng $d$ vẽ đoạn thẳng $AB = 10cm.$ Lấy điểm $N$ nằm giữa hai điểm $A,{\rm{ }}B$ và $AN = 2cm.$ Gọi $M$ là trung điểm của đoạn thẳng $BN,$ gọi $P$ là trung điểm của đoạn thẳng $MN.$ So sánh \(MP\) và \(AN.\)
-
A.
$MP < AN.$
-
B.
$MP > AN.$
-
C.
$MP = AN.$
-
D.
Không đủ điều kiện so sánh
Đáp án : C
+ Vì điểm $N$ nằm giữa hai điểm $A,{\rm{ }}B\;$
Áp dụng tính chất cộng độ dài đoạn thẳng để tính $NB$
+ Vì $M$ là trung điểm của đoạn thẳng $NB$ nên tính được $MN$ dựa vào tính chất trung điểm của đoạn thẳng
+ Vì $P$ là trung điểm của $MN$ nên tính được $NP$ dựa vào tính chất trung điểm của đoạn thẳng
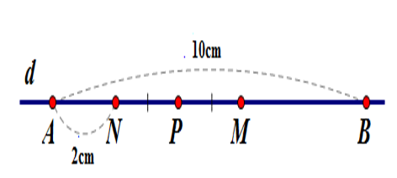
Vì điểm $N$ nằm giữa hai điểm $A,{\rm{ }}B\;$
nên $AN + NB = AB \Rightarrow NB = AB - AN = 10 - 2 = 8cm$
Vì $M$ là trung điểm của đoạn thẳng $NB$ nên $MN = \dfrac{1}{2}NB = \dfrac{1}{2}.8 = 4cm$
Vì $P$ là trung điểm của $MN$ nên $MP = \dfrac{1}{2}NM = \dfrac{1}{2}.4 = 2cm$
Suy ra $MP = 2cm;AN = 2cm$ nên $MP = AN.$
Trên tia $Ox$ lấy các điểm $M,{\rm{ }}N$ sao cho $OM = 2cm;ON = 3cm.$Trên tia đối của tia $NO$ lấy điểm $P$ sao cho $NP = 1cm.$
Tính độ dài các đoạn thẳng $MN$ và $MP.$
-
A.
$MN = 1cm;\,MP = 3cm$
-
B.
$MN = 2cm;\,MP = 3cm$
-
C.
$MN = 2cm;\,MP = 1cm$
-
D.
$MN = 1cm;\,MP = 2cm$
Đáp án: D
Sử dụng công thức cộng đoạn thẳng để tính độ dài các đoạn thẳng.

Vì hai điểm $M;N$ cùng thuộc tia $Ox$ mà $OM < ON\left( {2cm < 3cm} \right)$ nên điểm $M$ nằm giữa hai điểm $O$ và $N$.
Do đó $OM + MN = ON $ nên $MN = ON - OM$ $ = 3 - 2 = 1cm$
Vì hai tia $NP$ và $NO$ đối nhau mà $M$ nằm giữa hai điểm $O$ và $N$ nên $N$ là điểm nằm giữa $M$ và $P$
Do đó $MN + NP = MP$ hay $MP = 1 + 1 = 2cm$.
Vậy $MN = 1cm;\,MP = 2cm$.
Hãy chọn câu đúng nhất
-
A.
$N$ là trung điểm của đoạn thẳng $MP.$
-
B.
$M$ là trung điểm của đoạn thẳng $OP.$
-
C.
$M$ là trung điểm của đoạn thẳng $NP. $
-
D.
Cả A, B đều đúng.
Đáp án: D
Ta sử dụng kiến thức sau:
Nếu \(M\) nằm giữa \(A\) và \(B\) đồng thời \(MA = MB\) thì \(M\) là trung điểm của \(AB.\)

Từ câu trước và đề bài ta có $MN = 1cm;\,MP = 2cm;\,OM = 2cm;NP = 1cm$
Suy ra $MN = NP\left( { = 1cm} \right)\,\,\,\left( 1 \right);\,MP = OM\left( { = 2cm} \right)\,\left( 2 \right)$
Lại có $M$ nằm giữa hai điểm $O$ và $N$ mà $N$ nằm giữa hai điểm $M$ và $P$ nên điểm $M$ nằm giữa hai điểm $O$ và $P$ (3)
Từ (2) và (3) ta có $M$ là trung điểm đoạn $OP.$
Theo câu trước ta có $N$ là điểm nằm giữa $M$ và $P$ nên kết hợp với $\left( 1 \right)$ suy ra $N$ là trung điểm đoạn $MP$.
Nên cả A, B đều đúng.
Luyện tập và củng cố kiến thức Bài 36: Góc Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Xem chi tiết
Luyện tập và củng cố kiến thức Bài 37: Số đo góc Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Xem chi tiết
Luyện tập và củng cố kiến thức Bài tập cuối chương VIII Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Xem chi tiết
Luyện tập và củng cố kiến thức Bài 34: Đoạn thẳng. Độ dài đoạn thẳng Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Xem chi tiết
Luyện tập và củng cố kiến thức Bài 33: Điểm nằm giữa hai điểm. Tia Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Xem chi tiết
Luyện tập và củng cố kiến thức Bài 32: Điểm và đường thẳng Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Xem chi tiết

