Đề bài
Câu 1 :
Tính: \(\dfrac{1}{{12}} \cdot \dfrac{8}{{ - 9}}\)
-
A.
\(\dfrac{{ - 2}}{{27}}\)
-
B.
\(\dfrac{{ - 4}}{9}\)
-
C.
\(\dfrac{{ - 1}}{{18}}\)
-
D.
\(\dfrac{{ - 3}}{2}\)
Câu 2 :
Chọn câu đúng.
-
A.
\({\left( {\dfrac{{ - 7}}{6}} \right)^2} = \dfrac{{ - 49}}{{36}}\)
-
B.
\({\left( {\dfrac{2}{3}} \right)^3} = \dfrac{8}{9}\)
-
C.
\({\left( {\dfrac{2}{{ - 3}}} \right)^3} = \dfrac{8}{{ - 27}}\)
-
D.
\({\left( {\dfrac{{ - 2}}{3}} \right)^4} = \dfrac{{ - 16}}{{81}}\)
Câu 3 :
Có bao nhiêu giá trị nguyên dương của \(x\) thỏa mãn \({\left( {\dfrac{{ - 5}}{3}} \right)^3} < x < \dfrac{{ - 24}}{{35}}.\dfrac{{ - 5}}{6}\) ?
-
A.
$1$
-
B.
\(0\)
-
C.
\(2\)
-
D.
\(3\)
Câu 4 :
Giá trị nào dưới đây của \(x\) thỏa mãn $x\;:\;\dfrac{5}{8} = \dfrac{{ - 14}}{{35}} \cdot \dfrac{{15}}{{ - 42}}$
-
A.
$\dfrac{5}{{56}}$
-
B.
\(\dfrac{{ - 5}}{{56}}\)
-
C.
\(\dfrac{5}{{28}}\)
-
D.
\(\dfrac{{ - 5}}{{28}}\)
Câu 5 :
Có bao nhiêu giá trị của \(x\) thỏa mãn $\left( {\dfrac{7}{6} + x} \right):\dfrac{{16}}{{25}} = \dfrac{{ - 5}}{4}?$
-
A.
$\dfrac{{17}}{{30}}$
-
B.
\(\dfrac{{ - 11}}{{30}}\)
-
C.
\(\dfrac{{ - 59}}{{30}}\)
-
D.
\(\dfrac{{59}}{{30}}\)
Câu 6 :
Cho \(M = \dfrac{{17}}{5}.\dfrac{{ - 31}}{{125}}.\dfrac{1}{2}.\dfrac{{10}}{{17}}.{\left( {\dfrac{{ - 1}}{2}} \right)^3}\) và \(N = \left( {\dfrac{{17}}{{28}} + \dfrac{{28}}{{29}} - \dfrac{{19}}{{30}} - \dfrac{{20}}{{31}}} \right).\left( {\dfrac{{ - 5}}{{12}} + \dfrac{1}{4} + \dfrac{1}{6}} \right)\). Khi đó tổng \(M + N\) bằng
-
A.
$\dfrac{{ - 62}}{{125}}$
-
B.
\(\dfrac{{31}}{{1000}}\)
-
C.
\(\dfrac{{ - 31}}{{100}}\)
-
D.
\(\dfrac{{31}}{{100}}\)
Câu 7 :
Tính: \(B = \dfrac{{{2^2}}}{3} \cdot \dfrac{{{3^2}}}{8} \cdot \dfrac{{{4^2}}}{{15}} \cdot \dfrac{{{5^2}}}{{24}} \cdot \dfrac{{{6^2}}}{{35}} \cdot \dfrac{{{7^2}}}{{48}} \cdot \dfrac{{{8^2}}}{{63}} \cdot \dfrac{{{9^2}}}{{80}}\) ta được
-
A.
$\dfrac{9}{5}$
-
B.
\(\dfrac{3}{5}\)
-
C.
\(3\)
-
D.
\(\dfrac{6}{5}\)
Câu 8 :
Tìm số tự nhiên \(x\) biết \(\dfrac{1}{3} + \dfrac{1}{6} + \dfrac{1}{{10}} + ... + \dfrac{1}{{x\left( {x + 1} \right):2}} = \dfrac{{2019}}{{2021}}\)
-
A.
\(\dfrac{{2019}}{{2021}}\)
-
B.
\(2021\)
-
C.
\(2020\)
-
D.
\(2019\)
Câu 9 :
Tính \(M = 1 + \dfrac{1}{2} + \dfrac{1}{{{2^2}}} + \dfrac{1}{{{2^3}}} + ... + \dfrac{1}{{{2^{99}}}} + \dfrac{2}{{{2^{100}}}}\)
-
A.
\(\dfrac{1}{{{2^{99}}}}\)
-
B.
\(\dfrac{{{2^{101}} - 2}}{{{2^{100}}}}\)
-
C.
\(\dfrac{{{2^{101}} + 1}}{{{2^{100}}}}\)
-
D.
\(\dfrac{{{2^{101}} - 1}}{{{2^{100}}}}\)
Câu 10 :
Để làm bánh caramen, Linh cần \(\dfrac{4}{5}\) cốc đường để làm được \(10\) cái bánh. Vậy muốn làm \(15\) cái bánh thì Linh cần bao nhiêu cốc đường?
-
A.
\(\dfrac{4}{5}\) cốc đường
-
B.
\(1\) cốc đường
-
C.
\(\dfrac{7}{5}\) cốc đường
-
D.
\(\dfrac{6}{5}\) cốc đường
Câu 11 :
Tính giá trị biểu thức sau theo cách hợp lí
\(\left( {\dfrac{{20}}{7}.\dfrac{{ - 4}}{{ - 5}}} \right) + \left( {\dfrac{{20}}{7}.\dfrac{3}{{ - 5}}} \right)\)
-
A.
\(\dfrac{4}{7}\)
-
B.
\(\dfrac{{ - 4}}{7}\)
-
C.
\( - 4\)
-
D.
\(\dfrac{{11}}{7}\)
Câu 12 :
Một hình chữ nhật có diện tích \(\dfrac{{48}}{{35}}\) \(m^2\) và có chiều dài là \(\dfrac{6}{5}\) m. Tính chiều rộng của hình chữ nhật đó.
-
A.
\(\dfrac{8}{7}\,\left( m \right)\)
-
B.
\(\dfrac{7}{8}\,\left( m \right)\)
-
C.
\(\dfrac{{36}}{7}\,\left( m \right)\)
-
D.
\(\dfrac{{18}}{7}\,\left( m \right)\)
Câu 13 :
Tính: \(\dfrac{{28}}{{15}}.\dfrac{1}{{{4^2}}}.3 + \left( {\dfrac{8}{{15}} - \dfrac{{69}}{{60}}.\dfrac{5}{{23}}} \right):\dfrac{{51}}{{54}}\)
-
A.
\(\dfrac{1}{3}\)
-
B.
\(\dfrac{{20}}{{13}}\)
-
C.
\(3\)
-
D.
\(\dfrac{{13}}{{20}}\)
Câu 14 :
Phân số nghịch đảo của số \( - 3\) là
-
A.
$1$
-
B.
\(3\)
-
C.
\(\dfrac{1}{{ - 3}}\)
-
D.
\(\dfrac{1}{3}\)
Câu 15 :
Kết quả của phép tính \(\dfrac{{\left( { - 7} \right)}}{6}:\left( { - \dfrac{{14}}{3}} \right)\) là phân số có tử số là
-
A.
$\dfrac{1}{4}$
-
B.
\(\dfrac{1}{2}\)
-
C.
\( - \dfrac{1}{2}\)
-
D.
\(1\)
Câu 16 :
Giá trị nào dưới đây của \(x\) thỏa mãn \(\left( { - \dfrac{3}{5}} \right).x = \dfrac{4}{{15}}\)?
-
A.
$ - \dfrac{1}{{10}}$
-
B.
\( - \dfrac{4}{9}\)
-
C.
\( - \dfrac{4}{3}\)
-
D.
\( - 4\)
Câu 17 :
Tính \(\dfrac{2}{3}:\dfrac{7}{{12}}:\dfrac{4}{{18}}\)
-
A.
$\dfrac{7}{{18}}$
-
B.
\(\dfrac{9}{{14}}\)
-
C.
\(\dfrac{{36}}{7}\)
-
D.
\(\dfrac{{18}}{7}\)
Câu 18 :
Giá trị biểu thức \(M = \dfrac{5}{6}:{\left( {\dfrac{5}{2}} \right)^2} + \dfrac{7}{{15}}\) là phân số tối giản có dạng \(\dfrac{a}{b}\) với \(a > 0.\) Tính \(b + a.\)
-
A.
$8$
-
B.
\(\dfrac{9}{5}\)
-
C.
\(\dfrac{3}{5}\)
-
D.
\(2\)
Câu 19 :
Rút gọn \(N = \dfrac{{\dfrac{4}{{17}} - \dfrac{4}{{49}} - \dfrac{4}{{131}}}}{{\dfrac{3}{{17}} - \dfrac{3}{{49}} - \dfrac{3}{{131}}}}\) ta được
-
A.
$\dfrac{4}{3}$
-
B.
\(1\)
-
C.
\(0\)
-
D.
\( - \dfrac{4}{3}\)
Câu 20 :
Cho \(P = \left( {\dfrac{7}{{20}} + \dfrac{{11}}{{15}} - \dfrac{{15}}{{12}}} \right):\left( {\dfrac{{11}}{{20}} - \dfrac{{26}}{{45}}} \right)\) và \(Q = \dfrac{{5 - \dfrac{5}{3} + \dfrac{5}{9} - \dfrac{5}{{27}}}}{{8 - \dfrac{8}{3} + \dfrac{8}{9} - \dfrac{8}{{27}}}}:\dfrac{{15 - \dfrac{{15}}{{11}} + \dfrac{{15}}{{121}}}}{{16 - \dfrac{{16}}{{11}} + \dfrac{{16}}{{121}}}}\) . Chọn kết luận đúng:
-
A.
$P > Q$
-
B.
\(P < Q\)
-
C.
\(P < - Q\)
-
D.
\(P = Q\)
Câu 21 :
Tìm \(x\) biết \(\left( {x + \dfrac{1}{4} - \dfrac{1}{3}} \right):\left( {2 + \dfrac{1}{6} - \dfrac{1}{4}} \right) = \dfrac{7}{{46}}\)
-
A.
$\dfrac{9}{{64}}$
-
B.
\(\dfrac{9}{{16}}\)
-
C.
\(\dfrac{5}{{24}}\)
-
D.
\(\dfrac{3}{8}\)
Câu 22 :
Giá trị của \(x\) thỏa mãn \(\dfrac{{13}}{{15}} - \left( {\dfrac{{13}}{{21}} + x} \right).\dfrac{7}{{12}} = \dfrac{7}{{10}}?\)
-
A.
$ - \dfrac{1}{3}$
-
B.
\(\dfrac{6}{5}\)
-
C.
\( - \dfrac{3}{7}\)
-
D.
\(\dfrac{3}{7}\)
Câu 23 :
Một hình chữ nhật có diện tích là \(\dfrac{8}{{15}}\,\left( {c{m^2}} \right)\), chiều dài là \(\dfrac{4}{3}\,\left( {cm} \right)\). Tính chu vi hình chữ nhật đó.
-
A.
\(\dfrac{{52}}{5}\left( {cm} \right)\)
-
B.
\(\dfrac{{26}}{{15}}\left( {cm} \right)\)
-
C.
\(\dfrac{{52}}{{15}}\left( {cm} \right)\)
-
D.
\(\dfrac{{52}}{{15}}\left( {c{m^2}} \right)\)
Câu 24 :
Số các số nguyên \(x\) để \(\dfrac{{5x}}{3}:\dfrac{{10{x^2} + 5x}}{{21}}\) có giá trị là số nguyên là:
-
A.
$1$
-
B.
\(4\)
-
C.
\(2\)
-
D.
\(3\)
Câu 25 :
Một người đi xe máy, đi đoạn đường AB với vận tốc \(40km/h\) hết \(\dfrac{5}{4}\) giờ. Lúc về, người đó đi với vận tốc \(45km/h\). Tính thời gian người đó đi từ B về A?
-
A.
\(\dfrac{{10}}{9}\)
-
B.
\(\dfrac{{9}}{10}\)
-
C.
\(\dfrac{{11}}{9}\)
-
D.
\(2\)
Câu 26 :
Phân số \(\dfrac{a}{b}\) là phân số lớn nhất mà khi chia mỗi phân số \(\dfrac{{12}}{{35}};\) \(\dfrac{{18}}{{49}}\) cho \(\dfrac{a}{b}\) ta được kết quả là một số nguyên. Tính \(a + b.\)
-
A.
\(245\)
-
B.
\(251\)
-
C.
\(158\)
-
D.
\(496\)
Lời giải và đáp án
Câu 1 :
Tính: \(\dfrac{1}{{12}} \cdot \dfrac{8}{{ - 9}}\)
-
A.
\(\dfrac{{ - 2}}{{27}}\)
-
B.
\(\dfrac{{ - 4}}{9}\)
-
C.
\(\dfrac{{ - 1}}{{18}}\)
-
D.
\(\dfrac{{ - 3}}{2}\)
Đáp án : A
Muốn nhân hai phân số, ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số.
Khi nhân ta chú ý rút gọn phân số.
$\dfrac{1}{{12}} \cdot \dfrac{8}{{ - 9}} = \dfrac{{1.8}}{{12.\left( { - 9} \right)}}$$ = \dfrac{{1.2.4}}{{4.3.\left( { - 9} \right)}} = \dfrac{2}{{ - 27}} = \dfrac{{ - 2}}{{27}}$
Câu 2 :
Chọn câu đúng.
-
A.
\({\left( {\dfrac{{ - 7}}{6}} \right)^2} = \dfrac{{ - 49}}{{36}}\)
-
B.
\({\left( {\dfrac{2}{3}} \right)^3} = \dfrac{8}{9}\)
-
C.
\({\left( {\dfrac{2}{{ - 3}}} \right)^3} = \dfrac{8}{{ - 27}}\)
-
D.
\({\left( {\dfrac{{ - 2}}{3}} \right)^4} = \dfrac{{ - 16}}{{81}}\)
Đáp án : C
Thực hiện các phép tính ở mỗi đáp án rồi kết luận đáp án đúng.
Sử dụng nhận xét lũy thừa của một phân số:
Với \(n \in N\) thì \({\left( {\dfrac{a}{b}} \right)^n} = \underbrace {\dfrac{a}{b}.\dfrac{a}{b}...\dfrac{a}{b}}_{n\,\,{\rm{thừa}}\,{\rm{số}}} = \dfrac{{{a^n}}}{{{b^n}}}\)
Đáp án A: \({\left( {\dfrac{{ - 7}}{6}} \right)^2} = \dfrac{{{{\left( { - 7} \right)}^2}}}{{{6^2}}} = \dfrac{{49}}{{36}} \ne \dfrac{{ - 49}}{{36}}\) nên A sai.
Đáp án B: \({\left( {\dfrac{2}{3}} \right)^3} = \dfrac{{{2^3}}}{{{3^3}}} = \dfrac{8}{{27}} \ne \dfrac{8}{9}\) nên B sai.
Đáp án C: \({\left( {\dfrac{2}{{ - 3}}} \right)^3} = \dfrac{{{2^3}}}{{{{\left( { - 3} \right)}^3}}} = \dfrac{8}{{ - 27}}\) nên C đúng.
Đáp án D: \({\left( {\dfrac{{ - 2}}{3}} \right)^4} = \dfrac{{{{\left( { - 2} \right)}^4}}}{{{3^4}}} = \dfrac{{16}}{{81}} \ne \dfrac{{ - 16}}{{81}}\) nên D sai.
Câu 3 :
Có bao nhiêu giá trị nguyên dương của \(x\) thỏa mãn \({\left( {\dfrac{{ - 5}}{3}} \right)^3} < x < \dfrac{{ - 24}}{{35}}.\dfrac{{ - 5}}{6}\) ?
-
A.
$1$
-
B.
\(0\)
-
C.
\(2\)
-
D.
\(3\)
Đáp án : B
Thực hiện các phép tính rồi tìm \(x\)
Chú ý \(x\) nguyên dương nên \(x > 0\)
Vì \(x\) nguyên dương nên \(x > 0\)
mà \({\left( {\dfrac{{ - 5}}{3}} \right)^3} = \dfrac{{ - 125}}{{27}} < 0\) nên
\({\left( {\dfrac{{ - 5}}{3}} \right)^3} < 0 < x <\dfrac{{ - 24}}{{35}}.\dfrac{{ - 5}}{6} \)
Khi đó:
\(0 < x < \dfrac{{ - 24}}{{35}}.\dfrac{{ - 5}}{6}\)
\(0 < x < \dfrac{4}{7}\)
Vì \(\dfrac{4}{7} < 1\) nên \(0 < x < 1\) nên không có số nguyên dương nào thỏa mãn.
Câu 4 :
Giá trị nào dưới đây của \(x\) thỏa mãn $x\;:\;\dfrac{5}{8} = \dfrac{{ - 14}}{{35}} \cdot \dfrac{{15}}{{ - 42}}$
-
A.
$\dfrac{5}{{56}}$
-
B.
\(\dfrac{{ - 5}}{{56}}\)
-
C.
\(\dfrac{5}{{28}}\)
-
D.
\(\dfrac{{ - 5}}{{28}}\)
Đáp án : A
+ Tính vế phải theo qui tắc nhân phân số
+ Xác định rằng \(x\) là số bị chia bằng thương nhân với số chia
$\begin{array}{l}x\;:\;\dfrac{5}{8} = \dfrac{{ - 14}}{{35}} \cdot \dfrac{{15}}{{ - 42}}\\x:\dfrac{5}{8} = \dfrac{{ - 2}}{5}.\dfrac{5}{{ - 14}}\\x:\dfrac{5}{8} = \dfrac{1}{7}\\x = \dfrac{1}{7}.\dfrac{5}{8}\\x = \dfrac{5}{{56}}\end{array}$
Câu 5 :
Có bao nhiêu giá trị của \(x\) thỏa mãn $\left( {\dfrac{7}{6} + x} \right):\dfrac{{16}}{{25}} = \dfrac{{ - 5}}{4}?$
-
A.
$\dfrac{{17}}{{30}}$
-
B.
\(\dfrac{{ - 11}}{{30}}\)
-
C.
\(\dfrac{{ - 59}}{{30}}\)
-
D.
\(\dfrac{{59}}{{30}}\)
Đáp án : C
- Tìm \(\dfrac{7}{6} + x\) dựa vào quy tắc muốn tìm số bị chia, ta lấy thương nhân số chia.
- Chuyển vế, đổi dấu và tìm \(x\)
$\left( {\dfrac{7}{6} + x} \right):\dfrac{{16}}{{25}} = \dfrac{{ - 5}}{4}$
\(\dfrac{7}{6} + x = \dfrac{{ - 5}}{4}.\dfrac{{16}}{{25}}\)
\(\dfrac{7}{6} + x = \dfrac{{ - 1}}{1}.\dfrac{4}{5}\)
\(\dfrac{7}{6} + x = \dfrac{{ - 4}}{5}\)
\(x = \dfrac{{ - 4}}{5} - \dfrac{7}{6}\)
\(x = \dfrac{{ - 59}}{{30}}\)
Câu 6 :
Cho \(M = \dfrac{{17}}{5}.\dfrac{{ - 31}}{{125}}.\dfrac{1}{2}.\dfrac{{10}}{{17}}.{\left( {\dfrac{{ - 1}}{2}} \right)^3}\) và \(N = \left( {\dfrac{{17}}{{28}} + \dfrac{{28}}{{29}} - \dfrac{{19}}{{30}} - \dfrac{{20}}{{31}}} \right).\left( {\dfrac{{ - 5}}{{12}} + \dfrac{1}{4} + \dfrac{1}{6}} \right)\). Khi đó tổng \(M + N\) bằng
-
A.
$\dfrac{{ - 62}}{{125}}$
-
B.
\(\dfrac{{31}}{{1000}}\)
-
C.
\(\dfrac{{ - 31}}{{100}}\)
-
D.
\(\dfrac{{31}}{{100}}\)
Đáp án : B
Thực hiện tính giá trị của hai biểu thức \(M,N\) rồi tính tổng \(M + N\)
\(M = \dfrac{{17}}{5}.\dfrac{{ - 31}}{{125}}.\dfrac{1}{2}.\dfrac{{10}}{{17}}.{\left( {\dfrac{{ - 1}}{2}} \right)^3}\)
\(M = \dfrac{{17.\left( { - 31} \right).1.10.{{\left( { - 1} \right)}^3}}}{{{{5.125.2.17.2}^3}}}\)
\(M = \dfrac{{ - 31.\left( { - 1} \right)}}{{{{125.2}^3}}}\)
\(M = \dfrac{{31}}{{1000}}\)
\(N = \left( {\dfrac{{17}}{{28}} + \dfrac{{28}}{{29}} - \dfrac{{19}}{{30}} - \dfrac{{20}}{{31}}} \right).\left( {\dfrac{{ - 5}}{{12}} + \dfrac{1}{4} + \dfrac{1}{6}} \right)\)
\(N = \left( {\dfrac{{17}}{{28}} + \dfrac{{28}}{{29}} - \dfrac{{19}}{{30}} - \dfrac{{20}}{{31}}} \right).\left( {\dfrac{{ - 5}}{{12}} + \dfrac{3}{{12}} + \dfrac{2}{{12}}} \right)\)
\(N = \left( {\dfrac{{17}}{{28}} + \dfrac{{28}}{{29}} - \dfrac{{19}}{{30}} - \dfrac{{20}}{{31}}} \right).0\)
\(N = 0\)
Vậy \(M + N = \dfrac{{31}}{{1000}} + 0 = \dfrac{{31}}{{1000}}\)
Câu 7 :
Tính: \(B = \dfrac{{{2^2}}}{3} \cdot \dfrac{{{3^2}}}{8} \cdot \dfrac{{{4^2}}}{{15}} \cdot \dfrac{{{5^2}}}{{24}} \cdot \dfrac{{{6^2}}}{{35}} \cdot \dfrac{{{7^2}}}{{48}} \cdot \dfrac{{{8^2}}}{{63}} \cdot \dfrac{{{9^2}}}{{80}}\) ta được
-
A.
$\dfrac{9}{5}$
-
B.
\(\dfrac{3}{5}\)
-
C.
\(3\)
-
D.
\(\dfrac{6}{5}\)
Đáp án : A
Để nhân nhiều phân số, ta nhân các tử số lại với nhau, các mẫu số nhân lại với nhau, sau đó rút gọn phân số.
\(B = \dfrac{{{2^2}}}{3} \cdot \dfrac{{{3^2}}}{8} \cdot \dfrac{{{4^2}}}{{15}} \cdot \dfrac{{{5^2}}}{{24}} \cdot \dfrac{{{6^2}}}{{35}} \cdot \dfrac{{{7^2}}}{{48}} \cdot \dfrac{{{8^2}}}{{63}} \cdot \dfrac{{{9^2}}}{{80}}\)
\( = \dfrac{{2.2}}{{1.3}} \cdot \dfrac{{3.3}}{{2.4}} \cdot \dfrac{{4.4}}{{3.5}} \cdot \dfrac{{5.5}}{{4.6}} \cdot \dfrac{{6.6}}{{5.7}} \cdot \dfrac{{7.7}}{{6.8}} \cdot \dfrac{{8.8}}{{7.9}} \cdot \dfrac{{9.9}}{{8.10}}\)
\( = \dfrac{{2.3.4.5.6.7.8.9}}{{1.2.3.4.5.6.7.8}} \cdot \dfrac{{2.3.4.5.6.7.8.9}}{{3.4.5.6.7.8.9.10}}\)
\( = \dfrac{9}{1} \cdot \dfrac{2}{{10}} = \dfrac{{9.2}}{{1.10}} = \dfrac{9}{5}\)
Câu 8 :
Tìm số tự nhiên \(x\) biết \(\dfrac{1}{3} + \dfrac{1}{6} + \dfrac{1}{{10}} + ... + \dfrac{1}{{x\left( {x + 1} \right):2}} = \dfrac{{2019}}{{2021}}\)
-
A.
\(\dfrac{{2019}}{{2021}}\)
-
B.
\(2021\)
-
C.
\(2020\)
-
D.
\(2019\)
Đáp án : C
Đặt 2 làm nhân tử chung, rút gọn và tìm x
\(\begin{array}{l}\dfrac{1}{3} + \dfrac{1}{6} + \dfrac{1}{{10}} + ... + \dfrac{1}{{x\left( {x + 1} \right):2}} = \dfrac{{2019}}{{2021}}\\2.\left[ {\dfrac{1}{{2.3}} + \dfrac{1}{{3.4}} + ... + \dfrac{1}{{x(x + 1)}}} \right] = \dfrac{{2019}}{{2021}}\\2.\left( {\dfrac{1}{2} - \dfrac{1}{3} + \dfrac{1}{3} - \dfrac{1}{4} + ... + \dfrac{1}{x} - \dfrac{1}{{x + 1}}} \right) = \dfrac{{2019}}{{2021}}\\2.\left( {\dfrac{1}{2} - \dfrac{1}{{x + 1}}} \right) = \dfrac{{2019}}{{2021}}\\1 - \dfrac{2}{{x + 1}} = \dfrac{{2019}}{{2021}}\\\dfrac{2}{{x + 1}} = 1 - \dfrac{{2019}}{{2021}}\\\dfrac{2}{{x + 1}} = \dfrac{2}{{2021}}\\x + 1 = 2021\\x = 2020\end{array}\)
Câu 9 :
Tính \(M = 1 + \dfrac{1}{2} + \dfrac{1}{{{2^2}}} + \dfrac{1}{{{2^3}}} + ... + \dfrac{1}{{{2^{99}}}} + \dfrac{2}{{{2^{100}}}}\)
-
A.
\(\dfrac{1}{{{2^{99}}}}\)
-
B.
\(\dfrac{{{2^{101}} - 2}}{{{2^{100}}}}\)
-
C.
\(\dfrac{{{2^{101}} + 1}}{{{2^{100}}}}\)
-
D.
\(\dfrac{{{2^{101}} - 1}}{{{2^{100}}}}\)
Đáp án : D
Nhân hai vế của biểu thức cho 2
Khai triển biểu thức đưa về tính hợp lý
\(\begin{array}{l}M = 1 + \dfrac{1}{2} + \dfrac{1}{{{2^2}}} + \dfrac{1}{{{2^3}}} + ... + \dfrac{1}{{{2^{99}}}} + \dfrac{1}{{{2^{100}}}}\\2M = 2.\left( {1 + \dfrac{1}{2} + \dfrac{1}{{{2^2}}} + \dfrac{1}{{{2^3}}} + ... + \dfrac{1}{{{2^{99}}}} + \dfrac{1}{{{2^{100}}}}} \right)\\ = 2 + 1 + \dfrac{1}{2} + \dfrac{1}{{{2^2}}} + \dfrac{1}{{{2^3}}} + ... + \dfrac{1}{{{2^{99}}}}\end{array}\)
Ta có:
\(\begin{array}{l}M = 2M - M\\ = \left( {2 + 1 + \dfrac{1}{2} + \dfrac{1}{{{2^2}}} + \dfrac{1}{{{2^3}}} + ... + \dfrac{1}{{{2^{98}}}} + \dfrac{1}{{{2^{99}}}}} \right)\\ - \left( {1 + \dfrac{1}{2} + \dfrac{1}{{{2^2}}} + \dfrac{1}{{{2^3}}} + ... + \dfrac{1}{{{2^{99}}}} + \dfrac{1}{{{2^{100}}}}} \right)\\ = 2-\dfrac{1}{{{2^{100}}}} \\ =\dfrac{{{2^{101}} - 1}}{{{2^{100}}}} \end{array}\)
Câu 10 :
Để làm bánh caramen, Linh cần \(\dfrac{4}{5}\) cốc đường để làm được \(10\) cái bánh. Vậy muốn làm \(15\) cái bánh thì Linh cần bao nhiêu cốc đường?
-
A.
\(\dfrac{4}{5}\) cốc đường
-
B.
\(1\) cốc đường
-
C.
\(\dfrac{7}{5}\) cốc đường
-
D.
\(\dfrac{6}{5}\) cốc đường
Đáp án : D
Xác định để làm một cái bánh cần bao nhiêu phần cốc đường
Suy ra muốn làm 15 cái bánh thì cần bao nhiêu cốc đường.
Để làm một cái bánh thì cần lượng đường là: \(\dfrac{4}{5}.\dfrac{1}{{10}} = \dfrac{4}{{50}}\) (cốc đường)
Để làm 15 cái bánh thì cần số cốc đường là: \(\dfrac{4}{{50}}.15 = \dfrac{{60}}{{50}} = \dfrac{6}{5}\) (cốc đường)
Câu 11 :
Tính giá trị biểu thức sau theo cách hợp lí
\(\left( {\dfrac{{20}}{7}.\dfrac{{ - 4}}{{ - 5}}} \right) + \left( {\dfrac{{20}}{7}.\dfrac{3}{{ - 5}}} \right)\)
-
A.
\(\dfrac{4}{7}\)
-
B.
\(\dfrac{{ - 4}}{7}\)
-
C.
\( - 4\)
-
D.
\(\dfrac{{11}}{7}\)
Đáp án : A
Áp dụng tính chất: \(a.b + a.c = a.(b + c)\)
\(\begin{array}{l}\left( {\dfrac{{20}}{7}.\dfrac{{ - 4}}{{ - 5}}} \right) + \left( {\dfrac{{20}}{7}.\dfrac{3}{{ - 5}}} \right)\\ = \dfrac{{20}}{7}.\left( {\dfrac{{ - 4}}{{ - 5}} + \dfrac{3}{{ - 5}}} \right)\\ = \dfrac{{20}}{7}.\left( {\dfrac{{ - 1}}{{ - 5}}} \right)\\ = \dfrac{{20}}{7}.\dfrac{1}{5}\\ = \dfrac{{20}}{{35}} = \dfrac{4}{7}\end{array}\)
Câu 12 :
Một hình chữ nhật có diện tích \(\dfrac{{48}}{{35}}\) \(m^2\) và có chiều dài là \(\dfrac{6}{5}\) m. Tính chiều rộng của hình chữ nhật đó.
-
A.
\(\dfrac{8}{7}\,\left( m \right)\)
-
B.
\(\dfrac{7}{8}\,\left( m \right)\)
-
C.
\(\dfrac{{36}}{7}\,\left( m \right)\)
-
D.
\(\dfrac{{18}}{7}\,\left( m \right)\)
Đáp án : A
Diện tích hình chữ nhật = Chiều dài . chiều rộng
=> Chiều rộng = Diện tích : Chiều dài
Chiều rộng của hình chữ nhật là:
\(\dfrac{{48}}{{35}}:\dfrac{6}{5} = \dfrac{{48}}{{35}}.\dfrac{5}{6} = \dfrac{{6.8}}{{7.5}}.\dfrac{5}{6} = \dfrac{8}{7}\) (m)
Câu 13 :
Tính: \(\dfrac{{28}}{{15}}.\dfrac{1}{{{4^2}}}.3 + \left( {\dfrac{8}{{15}} - \dfrac{{69}}{{60}}.\dfrac{5}{{23}}} \right):\dfrac{{51}}{{54}}\)
-
A.
\(\dfrac{1}{3}\)
-
B.
\(\dfrac{{20}}{{13}}\)
-
C.
\(3\)
-
D.
\(\dfrac{{13}}{{20}}\)
Đáp án : D
Thực hiện phép tính theo thứ tự: Lũy thừa => Phép tính trong ngoặc => Nhân, chia => Cộng, trừ.
\(\begin{array}{l}\dfrac{{28}}{{15}}.\dfrac{1}{{{4^2}}}.3 + \left( {\dfrac{8}{{15}} - \dfrac{{69}}{{60}}.\dfrac{5}{{23}}} \right):\dfrac{{51}}{{54}}\\ = \dfrac{{28.1.3}}{{{{15.4}^2}}} + \left( {\dfrac{8}{{15}} - \dfrac{{23.3}}{{4.3.5}}.\dfrac{5}{{23}}} \right).\dfrac{{54}}{{51}}\\ = \dfrac{{7.4.1.3}}{{3.5.4.4}} + \left( {\dfrac{8}{{15}} - \dfrac{1}{4}} \right).\dfrac{{54}}{{51}}\\ = \dfrac{7}{{20}} + \left( {\dfrac{{32}}{{60}} - \dfrac{{15}}{{60}}} \right).\dfrac{{54}}{{51}}\\ = \dfrac{7}{{20}} + \dfrac{{17}}{{60}}.\dfrac{{54}}{{51}}\\ = \dfrac{7}{{20}} + \dfrac{{17}}{{6.10}}.\dfrac{{6.3.3}}{{17.3}}\\ = \dfrac{7}{{20}} + \dfrac{3}{{10}}\\ = \dfrac{7}{{20}} + \dfrac{6}{{20}}\\ = \dfrac{{13}}{{20}}\end{array}\)
Câu 14 :
Phân số nghịch đảo của số \( - 3\) là
-
A.
$1$
-
B.
\(3\)
-
C.
\(\dfrac{1}{{ - 3}}\)
-
D.
\(\dfrac{1}{3}\)
Đáp án : C
+ Phân số nghịch đảo của số nguyên \(a\,\left( {a \ne 0} \right)\) là \(\dfrac{1}{a}.\)
Phân số nghịch đảo của số \( - 3\) là \(\dfrac{1}{{ - 3}}\)
Câu 15 :
Kết quả của phép tính \(\dfrac{{\left( { - 7} \right)}}{6}:\left( { - \dfrac{{14}}{3}} \right)\) là phân số có tử số là
-
A.
$\dfrac{1}{4}$
-
B.
\(\dfrac{1}{2}\)
-
C.
\( - \dfrac{1}{2}\)
-
D.
\(1\)
Đáp án : D
Muốn chia hai phân số, ta lấy phân số thứ nhất nhân với nghịch đảo của phân số thứ hai.
\(\dfrac{{\left( { - 7} \right)}}{6}:\left( { - \dfrac{{14}}{3}} \right) = \dfrac{{ - 7}}{6}.\dfrac{{ - 3}}{{14}} = \dfrac{{1.1}}{{2.2}} = \dfrac{1}{4}\)
Phân số này có tử số là 1.
Câu 16 :
Giá trị nào dưới đây của \(x\) thỏa mãn \(\left( { - \dfrac{3}{5}} \right).x = \dfrac{4}{{15}}\)?
-
A.
$ - \dfrac{1}{{10}}$
-
B.
\( - \dfrac{4}{9}\)
-
C.
\( - \dfrac{4}{3}\)
-
D.
\( - 4\)
Đáp án : B
Muốn tìm thừa số chưa biết trong phép nhân, ta lấy tích chia cho thừa số đã biết.
\(\begin{array}{l}\left( { - \dfrac{3}{5}} \right).x = \dfrac{4}{{15}}\\x = \dfrac{4}{{15}}:\left( {\dfrac{{ - 3}}{5}} \right)\\x = \dfrac{4}{{15}}.\dfrac{5}{{ - 3}}\\x = - \dfrac{4}{9}\end{array}\)
Câu 17 :
Tính \(\dfrac{2}{3}:\dfrac{7}{{12}}:\dfrac{4}{{18}}\)
-
A.
$\dfrac{7}{{18}}$
-
B.
\(\dfrac{9}{{14}}\)
-
C.
\(\dfrac{{36}}{7}\)
-
D.
\(\dfrac{{18}}{7}\)
Đáp án : C
Trong biểu thức chỉ chứa nhân, chia, ta thực hiện từ trái qua phải.
Chú ý: Muốn chia hai phân số, ta thực hiện nhân phân số thứ nhất với nghịch đảo của phân số thứ hai.
\(\begin{array}{l}\dfrac{2}{3}:\dfrac{7}{{12}}:\dfrac{4}{{18}}\\ = \left( {\dfrac{2}{3}:\dfrac{7}{{12}}} \right):\dfrac{4}{{18}}\\ = \left( {\dfrac{2}{3}.\dfrac{{12}}{7}} \right):\dfrac{4}{{18}}\\ = \dfrac{8}{7}:\dfrac{4}{{18}}\\ = \dfrac{8}{7}.\dfrac{{18}}{4}\\ = \dfrac{{36}}{7}\end{array}\)
Sau này khi thực hiện một dãy các phép chia liên tiến, các em có thể thực hiện nhân nghịch đảo các phân số sau dấu chia được luôn, ví dụ trong bài toán này:
\(\dfrac{2}{3}:\dfrac{7}{{12}}:\dfrac{4}{{18}} = \dfrac{2}{3}.\dfrac{{12}}{7}.\dfrac{{18}}{4}\)\( = \dfrac{{2.12.18}}{{3.7.4}} = \dfrac{{2.3.6}}{{1.7.1}} = \dfrac{{36}}{7}\)
Rõ ràng các bước tính toán đã được rút gọn khá nhiều.
Câu 18 :
Giá trị biểu thức \(M = \dfrac{5}{6}:{\left( {\dfrac{5}{2}} \right)^2} + \dfrac{7}{{15}}\) là phân số tối giản có dạng \(\dfrac{a}{b}\) với \(a > 0.\) Tính \(b + a.\)
-
A.
$8$
-
B.
\(\dfrac{9}{5}\)
-
C.
\(\dfrac{3}{5}\)
-
D.
\(2\)
Đáp án : A
Trong biểu thức chỉ chứa các toán cộng trừ nhân chia, ta thực hiện nhân chia trước, cộng trừ sau.
\(\begin{array}{l}M = \dfrac{5}{6}:{\left( {\dfrac{5}{2}} \right)^2} + \dfrac{7}{{15}}\\M = \dfrac{5}{6}:\dfrac{{25}}{4} + \dfrac{7}{{15}}\\M = \dfrac{5}{6}.\dfrac{4}{{25}} + \dfrac{7}{{15}}\\M = \dfrac{{1.2}}{{3.5}} + \dfrac{7}{{15}}\\M = \dfrac{2}{{15}} + \dfrac{7}{{15}}\\M = \dfrac{9}{{15}} = \dfrac{3}{5}\end{array}\)
Khi đó \(a = 3,b = 5\) nên \(a + b = 8\)
Câu 19 :
Rút gọn \(N = \dfrac{{\dfrac{4}{{17}} - \dfrac{4}{{49}} - \dfrac{4}{{131}}}}{{\dfrac{3}{{17}} - \dfrac{3}{{49}} - \dfrac{3}{{131}}}}\) ta được
-
A.
$\dfrac{4}{3}$
-
B.
\(1\)
-
C.
\(0\)
-
D.
\( - \dfrac{4}{3}\)
Đáp án : A
Biến đổi tử và mẫu của \(N\) về dạng tích, rút gọn các thừa số chung của cả tử và mẫu rồi kết luận.
\(N = \dfrac{{\dfrac{4}{{17}} - \dfrac{4}{{49}} - \dfrac{4}{{131}}}}{{\dfrac{3}{{17}} - \dfrac{3}{{49}} - \dfrac{3}{{131}}}}\)\( = \dfrac{{4.\dfrac{1}{{17}} - 4.\dfrac{1}{{49}} - 4.\dfrac{1}{{131}}}}{{3.\dfrac{1}{{17}} - 3.\dfrac{1}{{49}} - 3.\dfrac{1}{{131}}}}\) \( = \dfrac{{4.\left( {\dfrac{1}{{17}} - \dfrac{1}{{49}} - \dfrac{1}{{131}}} \right)}}{{3.\left( {\dfrac{1}{{17}} - \dfrac{1}{{49}} - \dfrac{1}{{131}}} \right)}} = \dfrac{4}{3}\)
Câu 20 :
Cho \(P = \left( {\dfrac{7}{{20}} + \dfrac{{11}}{{15}} - \dfrac{{15}}{{12}}} \right):\left( {\dfrac{{11}}{{20}} - \dfrac{{26}}{{45}}} \right)\) và \(Q = \dfrac{{5 - \dfrac{5}{3} + \dfrac{5}{9} - \dfrac{5}{{27}}}}{{8 - \dfrac{8}{3} + \dfrac{8}{9} - \dfrac{8}{{27}}}}:\dfrac{{15 - \dfrac{{15}}{{11}} + \dfrac{{15}}{{121}}}}{{16 - \dfrac{{16}}{{11}} + \dfrac{{16}}{{121}}}}\) . Chọn kết luận đúng:
-
A.
$P > Q$
-
B.
\(P < Q\)
-
C.
\(P < - Q\)
-
D.
\(P = Q\)
Đáp án : A
Thực hiện tính giá trị các biểu thức \(P\) và \(Q\) rồi so sánh.
Chú ý: Trong biểu thức có chứa dấu ngoặc, ta ưu tiên thực hiện phép tính trong ngoặc trước, ngoài ngặc sau.
Biểu thức phức tạp nếu rút gọn được thì ta rút gọn nó trước rồi thực hiện tính toán.
\(P = \left( {\dfrac{7}{{20}} + \dfrac{{11}}{{15}} - \dfrac{{15}}{{12}}} \right):\left( {\dfrac{{11}}{{20}} - \dfrac{{26}}{{45}}} \right)\)
\(P = \left( {\dfrac{{21}}{{60}} + \dfrac{{44}}{{60}} - \dfrac{{75}}{{60}}} \right):\left( {\dfrac{{99}}{{180}} - \dfrac{{104}}{{180}}} \right)\)
\(P = \dfrac{{ - 10}}{{60}}:\dfrac{{ - 5}}{{180}} = \dfrac{{ - 10}}{{60}}.\dfrac{{180}}{{ - 5}} = 6\)
\(Q = \dfrac{{5 - \dfrac{5}{3} + \dfrac{5}{9} - \dfrac{5}{{27}}}}{{8 - \dfrac{8}{3} + \dfrac{8}{9} - \dfrac{8}{{27}}}}:\dfrac{{15 - \dfrac{{15}}{{11}} + \dfrac{{15}}{{121}}}}{{16 - \dfrac{{16}}{{11}} + \dfrac{{16}}{{121}}}}\)
\(Q = \dfrac{{5\left( {1 - \dfrac{1}{3} + \dfrac{1}{9} - \dfrac{1}{{27}}} \right)}}{{8\left( {1 - \dfrac{1}{3} + \dfrac{1}{9} - \dfrac{1}{{27}}} \right)}}:\dfrac{{15\left( {1 - \dfrac{1}{{11}} + \dfrac{1}{{121}}} \right)}}{{16\left( {1 - \dfrac{1}{{11}} + \dfrac{1}{{121}}} \right)}}\)
\(Q = \dfrac{5}{8}:\dfrac{{15}}{{16}} = \dfrac{5}{8}.\dfrac{{16}}{{15}} = \dfrac{2}{3}\)
Vì \(6 > \dfrac{2}{3}\) nên \(P > Q\)
Câu 21 :
Tìm \(x\) biết \(\left( {x + \dfrac{1}{4} - \dfrac{1}{3}} \right):\left( {2 + \dfrac{1}{6} - \dfrac{1}{4}} \right) = \dfrac{7}{{46}}\)
-
A.
$\dfrac{9}{{64}}$
-
B.
\(\dfrac{9}{{16}}\)
-
C.
\(\dfrac{5}{{24}}\)
-
D.
\(\dfrac{3}{8}\)
Đáp án : D
Thực hiện tính giá trị biểu thức trong ngoặc rồi sử dụng quy tắc tìm số bị chia trong phép chia, ta lấy thương nhân với số chia và quy tắc chuyển vế đổi dấu để tìm \(x\)
\(\left( {x + \dfrac{1}{4} - \dfrac{1}{3}} \right):\left( {2 + \dfrac{1}{6} - \dfrac{1}{4}} \right) = \dfrac{7}{{46}}\)
\(\left( {x + \dfrac{1}{4} - \dfrac{1}{3}} \right):\dfrac{{23}}{{12}} = \dfrac{7}{{46}}\)
\(x + \dfrac{1}{4} - \dfrac{1}{3} = \dfrac{7}{{46}}.\dfrac{{23}}{{12}}\)
\(x + \dfrac{1}{4} - \dfrac{1}{3} = \dfrac{7}{{24}}\)
\(x = \dfrac{7}{{24}} - \dfrac{1}{4} + \dfrac{1}{3}\)
\(x = \dfrac{3}{8}\)
Câu 22 :
Giá trị của \(x\) thỏa mãn \(\dfrac{{13}}{{15}} - \left( {\dfrac{{13}}{{21}} + x} \right).\dfrac{7}{{12}} = \dfrac{7}{{10}}?\)
-
A.
$ - \dfrac{1}{3}$
-
B.
\(\dfrac{6}{5}\)
-
C.
\( - \dfrac{3}{7}\)
-
D.
\(\dfrac{3}{7}\)
Đáp án : A
Áp dụng các kiến thức tìm số trừ trong phép trừ, tìm thừa số trong một tích và quy tắc chuyển vế đổi dấu để tìm \(x\)
\(\dfrac{{13}}{{15}} - \left( {\dfrac{{13}}{{21}} + x} \right).\dfrac{7}{{12}} = \dfrac{7}{{10}}\)
\(\left( {\dfrac{{13}}{{21}} + x} \right).\dfrac{7}{{12}} = \dfrac{{13}}{{15}} - \dfrac{7}{{10}}\)
\(\left( {\dfrac{{13}}{{21}} + x} \right).\dfrac{7}{{12}} = \dfrac{1}{6}\)
\(\dfrac{{13}}{{21}} + x = \dfrac{1}{6}:\dfrac{7}{{12}}\)
\(\dfrac{{13}}{{21}} + x = \dfrac{2}{7}\)
\(x = \dfrac{2}{7} - \dfrac{{13}}{{21}}\)
\(x = - \dfrac{1}{3}\)
Câu 23 :
Một hình chữ nhật có diện tích là \(\dfrac{8}{{15}}\,\left( {c{m^2}} \right)\), chiều dài là \(\dfrac{4}{3}\,\left( {cm} \right)\). Tính chu vi hình chữ nhật đó.
-
A.
\(\dfrac{{52}}{5}\left( {cm} \right)\)
-
B.
\(\dfrac{{26}}{{15}}\left( {cm} \right)\)
-
C.
\(\dfrac{{52}}{{15}}\left( {cm} \right)\)
-
D.
\(\dfrac{{52}}{{15}}\left( {c{m^2}} \right)\)
Đáp án : C
+ Tính chiều rộng hình chữ nhật bằng cách lấy diện tích chia cho chiều dài
+ Tính chu vi hình chữ nhật bằng cách lấy tổng chiều dài và chiều rộng tất cả nhân hai.
Chiều rộng hình chữ nhật là: \(\dfrac{8}{{15}}:\dfrac{4}{3} = \dfrac{2}{5}\left( {cm} \right)\)
Cho vi hình chữ nhật là: \(\left( {\dfrac{4}{3} + \dfrac{2}{5}} \right).2 = \dfrac{{52}}{{15}}\left( {cm} \right)\)
Một số em nhầm đơn vị chu vi nên chọn đáp án D là sai. Ở bài này chu vi có đơn vị là $cm$.
Câu 24 :
Số các số nguyên \(x\) để \(\dfrac{{5x}}{3}:\dfrac{{10{x^2} + 5x}}{{21}}\) có giá trị là số nguyên là:
-
A.
$1$
-
B.
\(4\)
-
C.
\(2\)
-
D.
\(3\)
Đáp án : B
- Rút gọn biểu thức đã cho.
- Biểu thức \(\dfrac{a}{{mx + n}}\) với \(a,m,n \in Z\) có giá trị là số nguyên nếu \(mx + n \in Ư\left( a \right)\)
\(\dfrac{{5x}}{3}:\dfrac{{10{x^2} + 5x}}{{21}}\) \( = \dfrac{{5x}}{3}.\dfrac{{21}}{{10{x^2} + 5x}}\) \( = \dfrac{{5x.21}}{{3.5x.\left( {2x + 1} \right)}}\) \( = \dfrac{7}{{2x + 1}}\)
Để biểu thức đã cho có giá trị là số nguyên thì \(\dfrac{7}{{2x + 1}}\) nguyên
Do đó \(2x + 1 \in Ư\left( 7 \right) = \left\{ { \pm 1; \pm 7} \right\}\)
Ta có bảng:
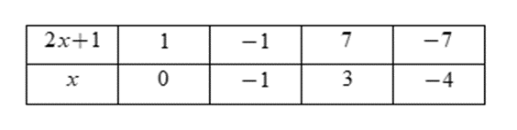
Vậy \(x \in \left\{ {0; - 1;3; - 4} \right\}\) suy ra có \(4\) giá trị thỏa mãn.
Một số em có thể sẽ quên mất hai ước nguyên âm là \( - 1\) và \( - 7\) nên chỉ chọn được hai giá trị.
Câu 25 :
Một người đi xe máy, đi đoạn đường AB với vận tốc \(40km/h\) hết \(\dfrac{5}{4}\) giờ. Lúc về, người đó đi với vận tốc \(45km/h\). Tính thời gian người đó đi từ B về A?
-
A.
\(\dfrac{{10}}{9}\)
-
B.
\(\dfrac{{9}}{10}\)
-
C.
\(\dfrac{{11}}{9}\)
-
D.
\(2\)
Đáp án : A
Tìm quãng đường AB
Tính thời gian đi từ A đến B: thời gian = quãng đường chia cho vận tốc
Quãng đường AB là: \(40.\dfrac{5}{4} = 50\) (km)
Thời gian người đó đi từ B về A là: \(\dfrac{{50}}{{45}} = \dfrac{{10}}{9}\) (giờ)
Câu 26 :
Phân số \(\dfrac{a}{b}\) là phân số lớn nhất mà khi chia mỗi phân số \(\dfrac{{12}}{{35}};\) \(\dfrac{{18}}{{49}}\) cho \(\dfrac{a}{b}\) ta được kết quả là một số nguyên. Tính \(a + b.\)
-
A.
\(245\)
-
B.
\(251\)
-
C.
\(158\)
-
D.
\(496\)
Đáp án : B
Lập luận để đưa về tính chia hết của tử và mẫu của phân số cần tìm.
Từ đó tìm được phân số và tính tổng của tử và mẫu.
Gọi phân số lớn nhất cần tìm là: \(\dfrac{a}{b}\) (\(a;b\) là nguyên tố cùng nhau)
Ta có: \(\dfrac{{12}}{{35}}:\dfrac{a}{b} = \dfrac{{12b}}{{35{\rm{a}}}}\) là số nguyên, mà \(12;35\) là nguyên tố cùng nhau
Nên \(12 \vdots a;b \vdots 35\)
Ta lại có: \(\dfrac{{18}}{{49}}:\dfrac{a}{b} = \dfrac{{18b}}{{49{\rm{a}}}}\) là số nguyên, mà \(18\) và \(49\) nguyên tố cùng nhau
Nên \(18 \vdots a;b \vdots 49\)
Để \(\dfrac{a}{b}\) lớn nhất ta có \(a = UCLN(12;18) = 6\) và \(b = BCNN(35;49) = 245\)
Vậy tổng \(a + b = 6 + 245 = 251\)
Luyện tập và củng cố kiến thức Bài 5: Số thập phân Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Xem chi tiết
Luyện tập và củng cố kiến thức Bài 6,7: Các phép tính với số thập phân Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Xem chi tiết
Luyện tập và củng cố kiến thức Bài 8: Ước lượng và làm tròn số Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Xem chi tiết
Luyện tập và củng cố kiến thức Bài 9: Tỉ số. Tỉ số phần trăm Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Xem chi tiết
Luyện tập và củng cố kiến thức Bài 10: Hai bài toán về phân số Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Xem chi tiết
Luyện tập và củng cố kiến thức Bài tập cuối chương V Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Xem chi tiết
Luyện tập và củng cố kiến thức Bài 4: Phép nhân, phép chia phân số Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Xem chi tiết
Luyện tập và củng cố kiến thức Các dạng toán về phép cộng, phép trừ phân số Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Xem chi tiết
Luyện tập và củng cố kiến thức Bài 3: Phép cộng, phép trừ phân số Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Xem chi tiết
Luyện tập và củng cố kiến thức Bài 2: Hỗn số dương Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Xem chi tiết
Luyện tập và củng cố kiến thức Bài 2: So sánh phân số Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Xem chi tiết
Luyện tập và củng cố kiến thức Các dạng toán về tính chất cơ bản của phân số Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Xem chi tiết
Luyện tập và củng cố kiến thức Tính chất cơ bản của phân số Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Xem chi tiết
Luyện tập và củng cố kiến thức Các dạng toán về phân số với tử và mẫu là số nguyên Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Xem chi tiết
Luyện tập và củng cố kiến thức Bài 1: Phân số với tử và mẫu là số nguyên Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Xem chi tiết

