Đề bài
Câu 1 :
Chọn phát biểu đúng nhất về định lí Pythagore:
-
A.
Trong một tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
-
B.
Trong một tam giác vuông, cạnh huyền bằng cạnh góc vuông.
-
C.
Trong tam giác vuông, bình phương cạnh huyền bằng bình phương cạnh góc vuông.
-
D.
Trong một tam giác vuông, bình phương cạnh huyền bằng tổng hai cạnh góc vuông.
Câu 2 :
Cho tam giác ABC vuông cân ở A. Tính độ dài BC biết AB = AC = 2 dm
-
A.
BC = 4 dm.
-
B.
\(BC = \sqrt {64} dm\).
-
C.
BC = 8 dm.
-
D.
\(BC = \sqrt 8 dm\)
Câu 3 :
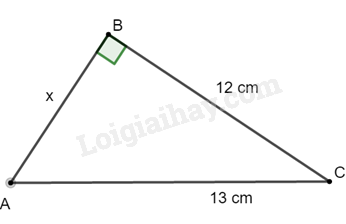
Cho hình vẽ. Tính x.
-
A.
x = 10 cm.
-
B.
x = 11 cm.
-
C.
x = 8 cm.
-
D.
x = 5 cm
Câu 4 :
Một tam giác vuông có cạnh huyền bằng 26cm độ dài các cạnh góc vuông tỉ lệ với 5 và 12. Tính độ dài các cạnh góc vuông.
-
A.
12cm ; 24cm.
-
B.
10cm ; 22 cm.
-
C.
10cm ; 24cm.
-
D.
15cm ; 24cm.
Câu 5 :
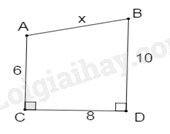
Cho hình vẽ sau. Tính \(x\).
-
A.
\(5\).
-
B.
\(5\sqrt 4 \).
-
C.
\(4\).
-
D.
\(4\sqrt 5 \).
Câu 6 :
Lựa chọn phương án đúng nhất:
-
A.
Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác nhọn.
-
B.
Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông.
-
C.
Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác tù.
-
D.
Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác cân.
Câu 7 :
Cho tam giác ABC vuông tại B, khi đó:
-
A.
\(A{B^2} + B{C^2} = A{C^2}\)
-
B.
\(A{B^2} - B{C^2} = A{C^2}\)
-
C.
\(A{B^2} + A{C^2} = B{C^2}\).
-
D.
\(A{B^2} = A{C^2} + B{C^2}\)
Câu 8 :
Tam giác ABC có AB = 3 cm, AC = 4cm, BC = 5cm. Tam giác ABC là tam giác gì?
-
A.
Tam giác nhọn
-
B.
Tam giác tù.
-
C.
Tam giác vuông.
-
D.
Không đủ dữ kiện để xác định
Câu 9 :
Cạnh huyền của một tam giác là bao nhiêu biết hai cạnh góc vuông là 3 và 4.
-
A.
8
-
B.
7
-
C.
6
-
D.
5
Câu 10 :
Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC tại H. Cho BH = 2cm, AB = 4cm. Tính AH:
-
A.
\(\sqrt {10} cm\).
-
B.
\(\sqrt {13} cm\).
-
C.
\(\sqrt {12} cm\).
-
D.
12 cm.
Câu 11 :
Tam giác nào là tam giác vuông trong các tam giác có độ dài ba cạnh như sau:
-
A.
15cm; 8cm; 18cm.
-
B.
21dm; 20dm; 29dm.
-
C.
5m; 6m; 8m.
-
D.
2m; 3m; 4m.
Câu 12 :
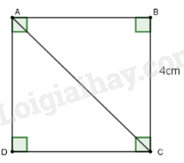
Cho ABCD là hình vuông cạnh 4 cm (hình vẽ). Khi đó độ dài đường chéo AC là:
-
A.
\(AC = 4\sqrt 2 cm\).
-
B.
\(AC = 4cm\).
-
C.
\(AC = \sqrt {30} cm\).
-
D.
\(AC = 8cm\).
Câu 13 :
Tìm câu sai trong các câu sau đây. Cho tam giác PQR vuông tại P. Khi đó:
-
A.
QR > PQ
-
B.
QR > PR
-
C.
\(Q{{{R}}^2} = P{Q^2} + P{{{R}}^2}\)
-
D.
\(Q{{{R}}^2} + P{{{R}}^2} = P{Q^2}\)
Câu 14 :
Cho tam giác ABC vuông ở A có AC = 20 cm. Kẻ \(AH \bot BC\). Biết BH = 9cm; HC = 16cm. Tính AB , AH
-
A.
AH = 12cm; AB = 15cm.
-
B.
AH = 10cm; AB = 15 cm.
-
C.
AH = 15cm; AB = 12cm.
-
D.
AH = 12cm; AB = 13 cm.
Câu 15 :
Cho tam giác ABC. Kẻ AH vuông góc với BC. Tính chu vi tam giác ABC biết AB = 5cm, AH = 4 cm, \(HC = \sqrt {184} cm\). (làm tròn đến chữ số thập phân thứ nhất).
-
A.
30,8cm.
-
B.
35, 7cm.
-
C.
31 cm.
-
D.
31, 7cm.
Câu 16 :
Tính cạnh huyền của một tam giác vuông biết tỉ số các cạnh góc vuông là 3 : 4 và chu vi tam giác là 36 cm
-
A.
9cm.
-
B.
12cm .
-
C.
15cm.
-
D.
16cm.
Câu 17 :
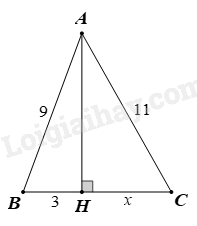
Tìm x trong hình vẽ sau:
-
A.
x = 6
-
B.
x = 7
-
C.
x = 8
-
D.
x = 5
Câu 18 :
Tìm x trong hình vẽ sau:
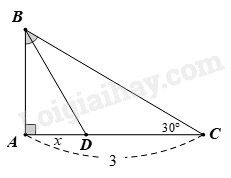
-
A.
x = 2
-
B.
x = 1,5
-
C.
x = 1
-
D.
x = 1,2
Câu 19 :
Tìm câu trả lời sai. Cho hình vẽ biết DE // HK. Khi đó:
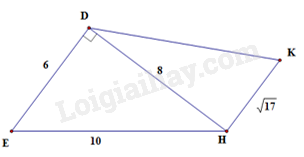
-
A.
DK = 9
-
B.
\(\widehat {E{{D}}H} = {90^o}\)
-
C.
DK = 10
-
D.
\(\widehat {DHK} = {90^o}\)
Câu 20 :
Cho tam giác ABC biết BC = 7,5cm; CA = 4,5cm, AB = 6cm. Độ dài đường cao AH của tam giác ABC là:
-
A.
12,96cm
-
B.
6,48cm
-
C.
3,6cm
-
D.
6,3cm
Câu 21 :
Cho tam giác ABC cân tại A biết AB = AC = 17cm. Kẻ \(B{\rm{D}} \bot AC\), biết BD = 15cm. Tính cạnh đáy BC.
-
A.
17 cm
-
B.
16 cm
-
C.
\(3\sqrt {14} \)cm
-
D.
\(3\sqrt {34} cm\)
Câu 22 :
Tính x trong hình sau:
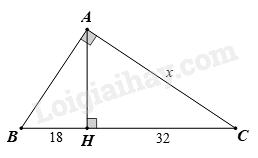
-
A.
36
-
B.
40
-
C.
42
-
D.
30
Câu 23 :
Cho tam giác ABC có \(\widehat B,\widehat C\) là các góc nhọn. Gọi H là chân đường vuông góc hạ từ A xuống BC. Biết AH = 6cm ; BH = 4,5cm và HC = 8cm. Khi đó tam giác ABC là tam giác gì?
-
A.
Tam giác cân
-
B.
Tam giác vuông
-
C.
Tam giác vuông cân
-
D.
Tam giác đều
Câu 24 :
Một tam giác có độ dài ba đường cao là 4,8cm ; 6cm ; 8cm. Tam giác đó là tam giác gì?
-
A.
Tam giác cân
-
B.
Tam giác vuông
-
C.
Tam giác vuông cân
-
D.
Tam giác đều
Lời giải và đáp án
Câu 1 :
Chọn phát biểu đúng nhất về định lí Pythagore:
-
A.
Trong một tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
-
B.
Trong một tam giác vuông, cạnh huyền bằng cạnh góc vuông.
-
C.
Trong tam giác vuông, bình phương cạnh huyền bằng bình phương cạnh góc vuông.
-
D.
Trong một tam giác vuông, bình phương cạnh huyền bằng tổng hai cạnh góc vuông.
Đáp án : A
Câu 2 :
Cho tam giác ABC vuông cân ở A. Tính độ dài BC biết AB = AC = 2 dm
-
A.
BC = 4 dm.
-
B.
\(BC = \sqrt {64} dm\).
-
C.
BC = 8 dm.
-
D.
\(BC = \sqrt 8 dm\)
Đáp án : D
Tam giác ABC vuông cân ở A nên theo định lý Pythagore ta có \(A{B^2} + A{C^2} = B{C^2}\) mà
AB = AC = 2 dm
Nên \(B{C^2} = {2^2} + {2^2} = 8 \Rightarrow BC = \sqrt 8 dm\)
Câu 3 :
Cho hình vẽ. Tính x.

-
A.
x = 10 cm.
-
B.
x = 11 cm.
-
C.
x = 8 cm.
-
D.
x = 5 cm
Đáp án : D
Áp dụng định lí Pythagore cho tam giác ABC vuông tại B ta được :
\(A{C^2} = A{B^2} + B{C^2} \)
\(A{B^2} = A{C^2} - B{C^2} \)
\({x^2} = {13^2} - {12^2} = 25 \)
\(x = 5cm\)
Vậy x = 5 cm
Câu 4 :
Một tam giác vuông có cạnh huyền bằng 26cm độ dài các cạnh góc vuông tỉ lệ với 5 và 12. Tính độ dài các cạnh góc vuông.
-
A.
12cm ; 24cm.
-
B.
10cm ; 22 cm.
-
C.
10cm ; 24cm.
-
D.
15cm ; 24cm.
Đáp án : C
Gọi độ dài hai cạnh góc vuông là \(x,y\left( {x,y > 0} \right)\)
Theo định lý Pytago ta có: \({x^2} + {y^2} = 26{}^2 \Rightarrow {x^2} + {y^2} = 676\)
Theo đề bài ta có: \(\frac{x}{5} = \frac{y}{{12}} \Rightarrow \frac{{{x^2}}}{{25}} = \frac{{{y^2}}}{{144}} = \frac{{{x^2} + {y^2}}}{{25 + 144}} = \frac{{676}}{{169}} = 4\)
Suy ra \({x^2} = 25.4 \Rightarrow {x^2} = 100 \Rightarrow x = 10cm\)
\({y^2} = 144.4 \Rightarrow {y^2} = 576 \Rightarrow y = 24cm\)
Câu 5 :
Cho hình vẽ sau. Tính \(x\).

-
A.
\(5\).
-
B.
\(5\sqrt 4 \).
-
C.
\(4\).
-
D.
\(4\sqrt 5 \).
Đáp án : D
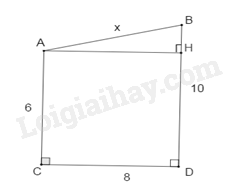
Kẻ \(AH \bot B{{D}}\) tại H.
Khi đó ACDH là hình chữ nhật, suy ra: HD = AC = 6; AH = CD = 8.
Do đó: BH = BD – HD = 10 – 6 = 4
Áp dụng định lí Pythagore cho tam giác AHB vuông tại H, ta có:
\(A{B^2} = B{H^2} + A{H^2} = {4^2} + {8^2} = 80\)
suy ra \(AB = 4\sqrt 5 \)
Vậy \(x = 4\sqrt 5 \)
Câu 6 :
Lựa chọn phương án đúng nhất:
-
A.
Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác nhọn.
-
B.
Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông.
-
C.
Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác tù.
-
D.
Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác cân.
Đáp án : B
Câu 7 :
Cho tam giác ABC vuông tại B, khi đó:
-
A.
\(A{B^2} + B{C^2} = A{C^2}\)
-
B.
\(A{B^2} - B{C^2} = A{C^2}\)
-
C.
\(A{B^2} + A{C^2} = B{C^2}\).
-
D.
\(A{B^2} = A{C^2} + B{C^2}\)
Đáp án : A
Vì tam giác ABC vuông tại B nên theo định lý Pythagore ta có \(A{B^2} + B{C^2} = A{C^2}\).
Câu 8 :
Tam giác ABC có AB = 3 cm, AC = 4cm, BC = 5cm. Tam giác ABC là tam giác gì?
-
A.
Tam giác nhọn
-
B.
Tam giác tù.
-
C.
Tam giác vuông.
-
D.
Không đủ dữ kiện để xác định
Đáp án : C
\(\begin{array}{l}A{B^2} + A{C^2} = {3^2} + {4^2} = 25\\B{C^2} = {5^2} = 25\\ \Rightarrow A{B^2} + A{C^2} = B{C^2}\end{array}\)
Vậy tam giác ABC là tam giác vuông
Câu 9 :
Cạnh huyền của một tam giác là bao nhiêu biết hai cạnh góc vuông là 3 và 4.
-
A.
8
-
B.
7
-
C.
6
-
D.
5
Đáp án : D
Câu 10 :
Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC tại H. Cho BH = 2cm, AB = 4cm. Tính AH:
-
A.
\(\sqrt {10} cm\).
-
B.
\(\sqrt {13} cm\).
-
C.
\(\sqrt {12} cm\).
-
D.
12 cm.
Đáp án : C
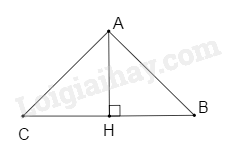
Áp dụng định lí Pythagore cho \(\Delta ABH\) vuông tại H ta có:
\(A{B^2} = B{H^2} + A{H^2} \)
suy ra \(A{H^2} = A{B^2} - B{H^2} = {4^2} - {2^2} = 12\)
nên \(AH = \sqrt {12} cm\)
Vậy \(AH = \sqrt {12} cm\)
Câu 11 :
Tam giác nào là tam giác vuông trong các tam giác có độ dài ba cạnh như sau:
-
A.
15cm; 8cm; 18cm.
-
B.
21dm; 20dm; 29dm.
-
C.
5m; 6m; 8m.
-
D.
2m; 3m; 4m.
Đáp án : B
+) Với bộ số: 15cm; 8cm; 18cm ta thấy : \({18^2} = 324{,^{}}{15^2} + {8^2} = 289 < 324\) nên loại đáp án A.
+) Với bộ số: 21dm; 20dm; 29dm ta thấy : \({29^2} = 841{;^{}}{21^2} + {20^2} = 841 = {29^2}\) nên đây là ba cạnh của tam giác vuông.
+) Với bộ số: 5m; 6m; 8m ta thấy : \({8^2} = 64{;^{}}{5^2} + {6^2} = 61 < 64\) nên loại đáp án C.
+) Với bộ số: 2m; 3m; 4m ta thấy : \({4^2} = 16{;^{}}{3^2} + {2^2} = 13 < 16\) nên loại đáp án D.
Câu 12 :
Cho ABCD là hình vuông cạnh 4 cm (hình vẽ). Khi đó độ dài đường chéo AC là:

-
A.
\(AC = 4\sqrt 2 cm\).
-
B.
\(AC = 4cm\).
-
C.
\(AC = \sqrt {30} cm\).
-
D.
\(AC = 8cm\).
Đáp án : A
Vì ABCD là hình vuông nên AB = AC = 4cm
Áp dụng định lý Pythagore: Trong một tam giác vuông, bình phương hai cạnh huyền bằng tổng bình phương hai cạnh góc vuông. cho tam giác ABC vuông tại B ta có
\(A{C^2} = A{B^2} + B{C^2} = {4^2} + {4^2} = 32 \Rightarrow AC = \sqrt {32} = 4\sqrt 2 cm\)
Câu 13 :
Tìm câu sai trong các câu sau đây. Cho tam giác PQR vuông tại P. Khi đó:
-
A.
QR > PQ
-
B.
QR > PR
-
C.
\(Q{{{R}}^2} = P{Q^2} + P{{{R}}^2}\)
-
D.
\(Q{{{R}}^2} + P{{{R}}^2} = P{Q^2}\)
Đáp án : D
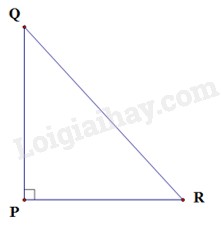
Tam giác PQR vuông tại P nên theo định lí Pythagore ta có: \(Q{{{R}}^2} = P{Q^2} + P{{{R}}^2}\) nên câu C đúng.
Vì độ dài đoạn thẳng là một số dương nên QR > PQ; QR > PR
Suy ra các câu A, B đúng.
Câu trả lời sai là câu D.
Câu 14 :
Cho tam giác ABC vuông ở A có AC = 20 cm. Kẻ \(AH \bot BC\). Biết BH = 9cm; HC = 16cm. Tính AB , AH
-
A.
AH = 12cm; AB = 15cm.
-
B.
AH = 10cm; AB = 15 cm.
-
C.
AH = 15cm; AB = 12cm.
-
D.
AH = 12cm; AB = 13 cm.
Đáp án : A
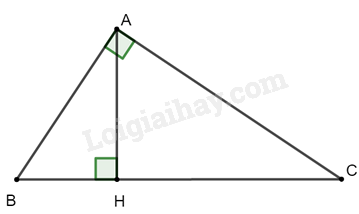
+) Ta có: BC = BH + HC = 9 + 16 = 25 cm
+) Xét tam giác ABC vuông tại A, theo định lí Pythagore ta có:
\(A{B^2} + A{C^2} = B{C^2} \Rightarrow A{B^2} = B{C^2} - A{C^2} = {25^2} - {20^2} = 225 \Rightarrow AB = 15cm\)
+) Xét tam giác ABH vuông tại H, theo định lí Pythagore ta có:
\(H{B^2} + H{A^2} = A{B^2} \Rightarrow A{H^2} = A{B^2} - H{B^2} = {15^2} - {9^2} = 144 \Rightarrow AH = 12cm\)
+) Vậy AH = 12cm ; AB = 15cm
Câu 15 :
Cho tam giác ABC. Kẻ AH vuông góc với BC. Tính chu vi tam giác ABC biết AB = 5cm, AH = 4 cm, \(HC = \sqrt {184} cm\). (làm tròn đến chữ số thập phân thứ nhất).
-
A.
30,8cm.
-
B.
35, 7cm.
-
C.
31 cm.
-
D.
31, 7cm.
Đáp án : B
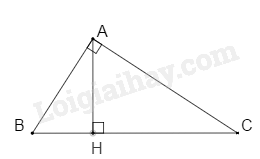
Áp dụng định lí Pythagore cho tam giác ABH vuông tại H, ta có:
\(\begin{array}{l}A{B^2} = B{H^2} + A{H^2} \Rightarrow B{H^2} = A{B^2} - A{H^2} = {5^2} - {4^2} = 9\\ \Rightarrow BH = 3(cm)\end{array}\)
Suy ra: \(BC = HB + HC = 3 + \sqrt {184} \)
Áp dụng định lí Pythagore cho tam giác AHC vuông tại H ta có:
\(A{C^2} = C{H^2} + A{H^2} = {4^2} + {\left( {\sqrt {184} } \right)^2} = 200 \Rightarrow AC = \sqrt {200} \)
Vậy chu vi tam giác ABC là: \(AB + AC + BC = 5 + \sqrt {200} + 3 + \sqrt {184} \approx 35,7cm\)
Câu 16 :
Tính cạnh huyền của một tam giác vuông biết tỉ số các cạnh góc vuông là 3 : 4 và chu vi tam giác là 36 cm
-
A.
9cm.
-
B.
12cm .
-
C.
15cm.
-
D.
16cm.
Đáp án : C
Gọi độ dài hai cạnh góc vuông là \(x,y\left( {y > x > 0} \right)\) (cm) và độ dài cạnh huyền là \(z\left( {z > y} \right)\)(cm)
Theo đề bài ta có \(\frac{x}{3} = \frac{y}{4}\) và x + y + z = 36
Đặt \(\frac{x}{3} = \frac{y}{4} = k\left( {k > 0} \right) \Rightarrow x = 3k;y = 4k\)
Theo định lý Pythagore ta có: \({x^2} + {y^2} = {z^2} \Rightarrow {z^2} = {\left( {3k} \right)^2} + {\left( {4k} \right)^2} = 25{k^2} = {\left( {5k} \right)^2} \Rightarrow z = 5k\)
Suy ra \(x + y + z = 3k + 4k + 5k = 12k = 36 \Rightarrow k = 3\) (thỏa mãn)
Từ đó: \(x{{ }} = {{ }}9{{ }}cm;{{ }}y{{ }} = {{ }}12{{ }}cm;{{ }}z{{ }} = {{ }}15cm.\)
Vậy cạnh huyền dài 15 cm
Câu 17 :
Tìm x trong hình vẽ sau:

-
A.
x = 6
-
B.
x = 7
-
C.
x = 8
-
D.
x = 5
Đáp án : B
Áp dụng định lý Pythagore: Trong một tam giác vuông, bình phương hai cạnh huyền bằng tổng bình phương hai cạnh góc vuông. vào Tam giác ABH vuông tại H ta có:
\(\begin{array}{l}A{B^2} = A{H^2} + B{H^2}\\ \Rightarrow A{H^2} = A{B^2} - B{H^2} = {9^2} - {3^2} = 72\end{array}\)
Áp dụng định lý Pythagore: Trong một tam giác vuông, bình phương hai cạnh huyền bằng tổng bình phương hai cạnh góc vuông. vào tam giác ACH vuông tại H ta có:
\(\begin{array}{l}A{C^2} = A{H^2} + H{C^2}\\ \Rightarrow H{C^2} = A{C^2} - A{H^2} = {11^2} - 72 = 49\\ \Rightarrow x = HC = \sqrt {49} = 7\end{array}\)
Câu 18 :
Tìm x trong hình vẽ sau:

-
A.
x = 2
-
B.
x = 1,5
-
C.
x = 1
-
D.
x = 1,2
Đáp án : C
Tam giác ABC vuông tại A nên \(\widehat {ABC} + \widehat {ACB} = {90^o} \) nên \(\widehat {ABC} = {90^o} - \widehat {ACB} = {90^o} - {30^o} = {60^o}\).
Lại có BD là tia phân giác của \(\widehat {ABC}\) (gỉa thiết) nên \(\widehat {AB{{D}}} = \widehat {DBC} = \frac{{\widehat {ABC}}}{2} = \frac{{{{60}^o}}}{2} = {30^o}\).
Tam giác ABC vuông tại A có \(\widehat {ACB} = {30^o}\) nên \(AB = \frac{1}{2}BC\) hay BC = 2 AB.
Áp dụng định lý Pythagore vào tam giác ABC vuông tại A ta có:
\(\begin{array}{l}B{C^2} = A{B^2} + A{C^2}\\ {\left( {2{{A}}B} \right)^2} = A{B^2} + {3^2}\\ 4{{A}}B = A{B^2} + 9\\ 3{{A}}{B^2} = 9\\ A{B^2} = 3\\ AB = \sqrt 3 \end{array}\)
Tam giác ABC vuông tại A có: \(\widehat {AB{{D}}} = {30^o}\) nên \(A{{D}} = \frac{1}{2}B{{D}}\) hay BD = 2AD.
Áp dụng định lý Pythagore vào tam giác ABD vuông tại A ta có:
\(\begin{array}{l}B{{{D}}^2} = A{B^2} + A{{{D}}^2}\\ {\left( {2{{AD}}} \right)^2} = A{B^2} + A{{{D}}^2}\\ {\left( {2x} \right)^2} = {\left( {\sqrt 3 } \right)^2} + {x^2}\\ 4{{{x}}^2} = 3 + {x^2}\\ 3{{{x}}^2} = 3\\ {x^2} = 1\\ x = 1\end{array}\)
Câu 19 :
Tìm câu trả lời sai. Cho hình vẽ biết DE // HK. Khi đó:

-
A.
DK = 9
-
B.
\(\widehat {E{{D}}H} = {90^o}\)
-
C.
DK = 10
-
D.
\(\widehat {DHK} = {90^o}\)
Đáp án : C
Ta có DE // HK nên: \(\widehat {E{{D}}H} = \widehat {DHK} = {90^o}\) (so le trong)
Áp dụng định lí Pythagore trong tam giác vuông DHK ta được:
\(D{K^2} = D{H^2} + H{K^2}\)
\(D{K^2} = {8^2} + {\left( {\sqrt {17} } \right)^2}\)
\(D{K^2} = 64 + 17 = 81 = {9^2}\\DK = 9\)
Câu 20 :
Cho tam giác ABC biết BC = 7,5cm; CA = 4,5cm, AB = 6cm. Độ dài đường cao AH của tam giác ABC là:
-
A.
12,96cm
-
B.
6,48cm
-
C.
3,6cm
-
D.
6,3cm
Đáp án : C
+ Áp dụng định lí Pythagore trong tam giác vuông.
+ Trong tam giác vuông, tích của hai cạnh góc vuông bằng tích của đường cao nhân với cạnh huyền.
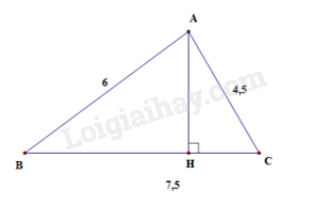
\(B{C^2} = {\left( {7,5} \right)^2} = 56,25\)
\(A{C^2} + A{B^2} = {\left( {4,5} \right)^2} + {6^2} = 56,25\)
Ta thấy: \(B{C^2} = A{B^2} + A{C^2}\)
Suy ra tam giác ABC vuông tại A.
Ta lại có: \(AB.AC = AH.BC \Rightarrow AH = \frac{{AB.AC}}{{BC}} = \frac{{6.4,5}}{{7,5}} = 3,6(cm)\)
Câu 21 :
Cho tam giác ABC cân tại A biết AB = AC = 17cm. Kẻ \(B{\rm{D}} \bot AC\), biết BD = 15cm. Tính cạnh đáy BC.
-
A.
17 cm
-
B.
16 cm
-
C.
\(3\sqrt {14} \)cm
-
D.
\(3\sqrt {34} cm\)
Đáp án : D
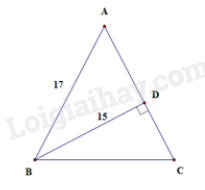
Tam giác ABD vuông tại D nên theo định lí Pythagore ta có: \(A{{\rm{D}}^2} = A{B^2} - B{{\rm{D}}^2} = {17^2} - {15^2} = 64 = {8^2} \)
nên \(A{\rm{D}} = 8(cm)\)
Suy ra \( C{\rm{D}} = AC - A{\rm{D}} = 17 - 8 = 9(cm)\)
Tam giác BCD vuông tại D nên theo định lí Pythagore ta có:
\(\begin{array}{l}B{C^2} = C{{\rm{D}}^2} - B{{\rm{D}}^2} = {9^2} + {15^2} = 81 + 225 = 306\end{array}\)
nên \(BC = 3\sqrt {34} (cm)\)
Câu 22 :
Tính x trong hình sau:

-
A.
36
-
B.
40
-
C.
42
-
D.
30
Đáp án : B
Áp dụng định lý Pythagore vào tam giác AHB vuông tại H ta có:
\(A{H^2} + B{H^2} = A{B^2} \Rightarrow A{H^2} = A{B^2} - B{H^2}(1)\)
Áp dụng định lý Pythagore vào tam giác AHC vuông tại H ta có:
\(A{H^2} + C{H^2} = A{C^2} \Rightarrow A{H^2} = A{C^2} - C{H^2} = (2)\)
Từ (1) và (2) ta có: \(A{B^2} - B{H^2} = A{C^2} - C{H^2}\)
\(\begin{array}{l} \Rightarrow A{B^2} - {18^2} = {x^2} - {32^2}\\ \Rightarrow A{B^2} = {x^2} - {32^2} + {18^2}\\ \Rightarrow A{B^2} = {x^2} - 1024 + 324\\ \Rightarrow A{B^2} = {x^2} - 700\end{array}\)
Ta có: BC = BH + CH = 18 + 32 = 50
Áp dụng định lý Pythagore vào tam giác ABC vuông tại A ta có:
\(\begin{array}{l}A{B^2} + A{C^2} = B{C^2}\\ \Rightarrow A{B^2} + {x^2} = {50^2}(3)\end{array}\)
Thay \(A{B^2} = {x^2} - 700\) vào (3) ta được:
\(\begin{array}{l}{x^2} - 700 + {{\rm{x}}^2} = {50^2}\\ \Rightarrow 2{{\rm{x}}^2} = 2500 + 700\\ \Rightarrow 2{{\rm{x}}^2} = 3200\\ \Rightarrow {x^2} = 3200:2 = 1600\\ \Rightarrow x = \sqrt {1600} = 40\end{array}\)
Câu 23 :
Cho tam giác ABC có \(\widehat B,\widehat C\) là các góc nhọn. Gọi H là chân đường vuông góc hạ từ A xuống BC. Biết AH = 6cm ; BH = 4,5cm và HC = 8cm. Khi đó tam giác ABC là tam giác gì?
-
A.
Tam giác cân
-
B.
Tam giác vuông
-
C.
Tam giác vuông cân
-
D.
Tam giác đều
Đáp án : B
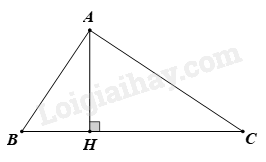
Áp dụng định lý Pythagore vào tam giác AHB vuông tại H ta có:
\(\begin{array}{l}A{B^2} = A{H^2} + B{H^2}\\ \Rightarrow AB = {6^2} + 4,{5^2} = 36 + \frac{{81}}{4} = \frac{{225}}{4}\end{array}\)
Áp dụng định lý Pythagore vào tam giác AHC vuông tại H ta có:
\(\begin{array}{l}A{C^2} = A{H^2} + H{C^2}\\ \Rightarrow A{C^2} = {6^2} + {8^2} = 100\end{array}\)
Ta có: \(BC = BH + HC = 4,5 + 8 = \frac{{25}}{2}\)
\( \Rightarrow B{C^2} = {\left( {\frac{{25}}{2}} \right)^2} = \frac{{625}}{4}(1)\)
Ta có: \(A{B^2} + A{C^2} = \frac{{225}}{4} + 100 = \frac{{625}}{4}(2)\)
Từ (1) và (2) suy ra: \(B{C^2} = A{B^2} + A{C^2}\)
Vậy tam giác ABC vuông tại A
Câu 24 :
Một tam giác có độ dài ba đường cao là 4,8cm ; 6cm ; 8cm. Tam giác đó là tam giác gì?
-
A.
Tam giác cân
-
B.
Tam giác vuông
-
C.
Tam giác vuông cân
-
D.
Tam giác đều
Đáp án : B
Gọi a, b, c lần lượt là độ dài ba cạnh của tam giác ứng với các đường cao theo thứ tự đã cho, S là diện tích của tam giác ABC \(\left( {a,b,c,S > 0} \right)\). Chứng minh \({a^2} = {b^2} + {c^2}\) suy ra tam giác ABC là tam giác vuông.
Gọi a, b, c lần lượt là độ dài ba cạnh của tam giác ứng với các đường cao theo thứ tự đã cho, S là diện tích của tam giác ABC \(\left( {a,b,c,S > 0} \right)\)
Ta có: \(S = \frac{1}{2}.4,8.a = \frac{1}{6}.6.b = \frac{1}{2}.8.c\) hay \(4,8{\rm{a}} = 6b = 8c = 2{\rm{S}}\)
Do đó: \(a = \frac{{2{\rm{S}}}}{{4,8}} = \frac{{5{\rm{S}}}}{{12}};b = \frac{{2{\rm{S}}}}{6} = \frac{S}{3};c = \frac{{2{\rm{S}}}}{8} = \frac{S}{4}\)
Ta có: \({b^2} + {c^2} = {\left( {\frac{S}{3}} \right)^2} + {\left( {\frac{S}{4}} \right)^2} = \frac{{{S^2}}}{9} + \frac{{{S^2}}}{{16}} = \frac{{25{{\rm{S}}^2}}}{{144}};{a^2} = {\left( {\frac{{5{\rm{S}}}}{{12}}} \right)^2} = \frac{{25{{\rm{S}}^2}}}{{144}}\)
Suy ra \({a^2} = {b^2} + {c^2}\) nên tam giác đã cho là tam giác vuông, đỉnh góc vuông ứng với đường cao có độ dài là 4,8cm
Luyện tập và củng cố kiến thức Bài 2: Tứ giác Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Xem chi tiết
Luyện tập và củng cố kiến thức Bài 3: Hình thang - Hình thang cân Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Xem chi tiết
Luyện tập và củng cố kiến thức Bài 4: Hình bình hành - Hình thoi Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Xem chi tiết
Luyện tập và củng cố kiến thức Bài 5: Hình chữ nhật - Hình vuông Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Xem chi tiết

