Đề bài
Câu 1 :
Phương trình với ẩn x có dạng:
-
A.
\(A\left( x \right) = B\left( x \right)\), trong đó vế trái A(x) và vế phải B(x) là hai biểu thức của cùng một biến x
-
B.
\(A\left( x \right) > B\left( x \right)\), trong đó vế trái A(x) và vế phải B(x) là hai biểu thức của cùng một biến x
-
C.
\(A\left( x \right) < B\left( x \right)\), trong đó vế trái A(x) và vế phải B(x) là hai biểu thức của cùng một biến x
-
D.
\(A\left( x \right) \ge B\left( x \right)\), trong đó vế trái A(x) và vế phải B(x) là hai biểu thức của cùng một biến x
Câu 2 :
Phương trình nào dưới đây là phương trình một ẩn?
-
A.
\(2x - 2y + 1 = 0\)
-
B.
\(xzy = 6\)
-
C.
\(2{x^2} + 1 = x - 2\)
-
D.
\(3{x^2} + 4{y^2} = 2y\)
Câu 3 :
\({x_0}\) được gọi là nghiệm của phương trình \(A\left( x \right) = B\left( x \right)\) nếu:
-
A.
\(A\left( {{x_0}} \right) < B\left( {{x_0}} \right)\)
-
B.
\(A\left( {{x_0}} \right) > B\left( {{x_0}} \right)\)
-
C.
\(A\left( {{x_0}} \right) \ne B\left( {{x_0}} \right)\)
-
D.
\(A\left( {{x_0}} \right) = B\left( {{x_0}} \right)\)
Câu 4 :
Phương trình dạng \(ax + b = 0\), với a, b là hai số đã cho được gọi là phương trình bậc nhất một ẩn x khi:
-
A.
Với mọi giá trị của a, b
-
B.
\(a \ne 0;b \ne 0\)
-
C.
\(a \ne 0\)
-
D.
\(b \ne 0\)
Câu 5 :
Cho phương trình \(2x + 1 = 0\), chọn khẳng định đúng
-
A.
Hệ số của x là 2, hạng tử tự do là 1
-
B.
Hệ số của x là 1, hạng tử tự do là 2
-
C.
Hệ số của x là \( - 1,\) hạng tử tự do là 2
-
D.
Hệ số của x là 2, hạng tử tự do là \( - 1\)
Câu 6 :
Nghiệm của phương trình \(3x - 6 = 0\) là:
-
A.
\(x = \frac{1}{2}\)
-
B.
\(x = \frac{{ - 1}}{2}\)
-
C.
\(x = 2\)
-
D.
\(x = - 2\)
Câu 7 :
Nghiệm của phương trình \(\frac{3}{4} + \frac{2}{5}x = 0\) có dạng \(x = - \frac{a}{b},\) trong đó \(b > 0\) và \(\frac{a}{b}\) là phân số tối giản. Khẳng định nào sau đây đúng?
-
A.
\(a + b = 21\)
-
B.
\(a + b = 23\)
-
C.
\(a + b = 20\)
-
D.
\(a + b = 24\)
Câu 8 :
Ở một số quốc gia, người ta dùng cả hai đơn vị đo nhiệt độ là Fahrenheit (oF) và độ Celcius (oC), liên hệ với nhau bởi công thức \(C = \frac{5}{9}\left( {F - 32} \right).\) Khi ở 20 oC thì ứng với độ Fahrenheit là:
-
A.
34 oF
-
B.
38 oF
-
C.
64 oF
-
D.
68 oF
Câu 9 :
Biết rằng \(4x - 8 = 0\). Giá trị của biểu thức \(5{x^2} - 4\) là:
-
A.
\( - 24\)
-
B.
\(24\)
-
C.
\( - 16\)
-
D.
16
Câu 10 :
Phương trình \({x^2} + 4 = 0\) có bao nhiêu nghiệm?
-
A.
Vô nghiệm
-
B.
Vô số nghiệm
-
C.
1 nghiệm
-
D.
2 nghiệm
Câu 11 :
Tìm x, biết rằng nếu lấy x trừ đi \(\frac{1}{4},\) rồi nhân kết quả với \(\frac{1}{2}\) thì được \(\frac{1}{8}\)
-
A.
\(x = \frac{1}{2}\)
-
B.
\(x = - \frac{1}{2}\)
-
C.
\(x = \frac{1}{4}\)
-
D.
\(x = \frac{{ - 1}}{4}\)
Câu 12 :
Gọi \({x_0}\) là nghiệm của phương trình \(3\left( {x - 5} \right) + 9x\left( {x - 3} \right) = 9{x^2}.\)
Hãy chọn đáp án đúng.
-
A.
\({x_0}
- B.
\({x_0}- C.
\({x_0} > 0\)- D.
\({x_0} > 1\)Câu 13 :
Cho \(A = \frac{{2\left( {x + 1} \right)}}{3} - \frac{1}{2},B = \frac{{1 + 3x}}{4}\). Tìm x để \(A = B\)
-
A.
\(x = 1\)
-
B.
\(x = - 1\)
-
C.
\(x = - 2\)
-
D.
\(x = 2\)
Câu 14 :
Cho hai phương trình \(8\left( {x - 2} \right) = 14 + 6\left( {x - 1} \right) + 2\left( {x + 5} \right)\,\,\left( 1 \right)\) và \({\left( {x - 2} \right)^2} = {x^2} - 2x - 2\left( {x - 2} \right)\;\;\left( 2 \right)\)
Hãy chọn đáp án đúng.
-
A.
Phương trình (1) vô nghiệm, phương trình (2) có nghiệm duy nhất
-
B.
Phương trình (1) có vô số nghiệm, phương trình (2) vô nghiệm
-
C.
Phương trình (1) vô nghiệm, phương trình (2) có vô số nghiệm
-
D.
Cả phương trình (1) và phương trình (2) đều có một nghiệm
Câu 15 :
Cho phương trình: \(\frac{{x - 11}}{{2011}} + \frac{{x - 10}}{{2012}} = \frac{{x - 74}}{{1948}} + \frac{{x - 72}}{{1950}}\).
Khẳng định nào sau đây đúng?
-
A.
Nghiệm của phương trình là một chia hết cho 5
-
B.
Nghiệm của phương trình là một số chia hết cho 2
-
C.
Nghiệm của phương trình là một chia hết cho 4
-
D.
Nghiệm của phương trình là một số nguyên tố
Câu 16 :
Tìm điều kiện của m để phương trình \(3mx + m - 4x = 3{m^2} + 1\) có nghiệm duy nhất
-
A.
\(m \ne \frac{4}{3}\)
-
B.
\(m = \frac{4}{3}\)
-
C.
\(m = \frac{3}{4}\)
-
D.
\(m \ne \frac{3}{4}\)
Câu 17 :
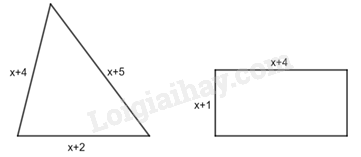
Hình tam giác và hình chữ nhật ở hình dưới có cùng chu vi. Khi đó, giá trị của x là:
-
A.
\(x = - 2\)
-
B.
\(x = 2\)
-
C.
\(x = 1\)
-
D.
\(x = - 1\)
Câu 18 :
Cho hai phương trình \(\frac{{7x}}{8} - 5\left( {x - 9} \right) = \frac{1}{6}\left( {20x + 1,5} \right)\left( 1 \right)\) và \(2\left( {a - 1} \right)x - a\left( {x - 1} \right) = 2a + 3\;\left( 2 \right)\)
Để phương trình (2) có một nghiệm bằng một phần ba nghiệm của phương trình (1) thì giá trị của a là:
-
A.
\(a = 7\)
-
B.
\(a = - 7\)
-
C.
\(a = \frac{1}{7}\)
-
D.
\(a = \frac{{ - 1}}{7}\)
Câu 19 :
Phương trình \(\frac{{x + 1}}{3} + \frac{{3\left( {2x + 1} \right)}}{4} = \frac{{2x + 3\left( {x + 1} \right)}}{6} + \frac{{7 + 12x}}{{12}}\) có bao nhiêu nghiệm?
-
A.
1 nghiệm
-
B.
2 nghiệm
-
C.
Không có nghiệm nào
-
D.
Có vô số nghiệm
Câu 20 :
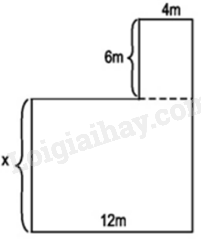
Cho hình vẽ dưới đây. Biết rằng diện tích của cả hình đó bằng \(168{m^2}.\) Khi đó, giá trị của x (mét) là:
-
A.
11m
-
B.
12m
-
C.
13m
-
D.
14m
Câu 21 :
Một xe máy khởi hành từ Hà Nội đi Hải Phòng với vận tốc trung bình 32km/h. Sau đó 1 giờ, một ô tô cũng khởi hành từ Hà Nội đi Hải Phòng, cùng đường với xe máy và với vận tốc trung bình 48km/h. Phương trình biểu thị việc ô tô gặp xe máy sau x giờ, kể từ khi ô tô khởi hành là:
-
A.
\(48 = 32\left( {x - 1} \right)\)
-
B.
\(48x = 32\left( {1 - x} \right)\)
-
C.
\(48x = 32\left( {x - 1} \right)\)
-
D.
\(48x = 32\left( {x + 1} \right)\)
Câu 22 :
Cho phương trình \(\left( {{m^2} - 3m + 2} \right)x = m - 2,\) với m là tham số. Giá trị của m để phương trình có vô số nghiệm là:
-
A.
\(m = 1\)
-
B.
\(m = 2\)
-
C.
\(m \in \left\{ {1;2} \right\}\)
-
D.
\(m = 0\)
Câu 23 :
Số nghiệm của phương trình \(\sqrt x + 1 = 2\sqrt { - x} \) là:
-
A.
1 nghiệm
-
B.
2 nghiệm
-
C.
0 nghiệm
-
D.
Vô số nghiệm
Câu 24 :
Hình dưới dây mô tả một đài phun nước. Tốc độ ban đầu của nước là 48 ft/s (ft là một đơn vị đo độ dài với 1ft=0,3048m). Tốc độ v(ft/s) của nước tại thời điểm t(s) được cho bởi công thức \(v = 48 - 30t.\) Thời gian để một giọt nước đi từ mặt đài phun nước đến khi đạt độ cao tối đa là:

-
A.
1,8s
-
B.
1,7s
-
C.
1,6s
-
D.
1,5s
Lời giải và đáp án
Câu 1 :
Phương trình với ẩn x có dạng:
-
A.
\(A\left( x \right) = B\left( x \right)\), trong đó vế trái A(x) và vế phải B(x) là hai biểu thức của cùng một biến x
-
B.
\(A\left( x \right) > B\left( x \right)\), trong đó vế trái A(x) và vế phải B(x) là hai biểu thức của cùng một biến x
-
C.
\(A\left( x \right) < B\left( x \right)\), trong đó vế trái A(x) và vế phải B(x) là hai biểu thức của cùng một biến x
-
D.
\(A\left( x \right) \ge B\left( x \right)\), trong đó vế trái A(x) và vế phải B(x) là hai biểu thức của cùng một biến x
Đáp án : A
Phương pháp giải :Sử dụng nhận biết phương trình một ẩn: Phương trình với ẩn x có dạng \(A\left( x \right) = B\left( x \right)\), trong đó vế trái A(x) và vế phải B(x) là hai biểu thức của cùng một biến x.Lời giải chi tiết :Phương trình với ẩn x có dạng \(A\left( x \right) = B\left( x \right)\), trong đó vế trái A(x) và vế phải B(x) là hai biểu thức của cùng một biến x.Câu 2 :
Phương trình nào dưới đây là phương trình một ẩn?
-
A.
\(2x - 2y + 1 = 0\)
-
B.
\(xzy = 6\)
-
C.
\(2{x^2} + 1 = x - 2\)
-
D.
\(3{x^2} + 4{y^2} = 2y\)
Đáp án : C
Phương pháp giải :Sử dụng nhận biết phương trình một ẩn: Phương trình với ẩn x có dạng \(A\left( x \right) = B\left( x \right)\), trong đó vế trái A(x) và vế phải B(x) là hai biểu thức của cùng một biến x.Lời giải chi tiết :\(2{x^2} + 1 = x - 2\) là phương trình một ẩn (ẩn x)
Lưu ý: Đề bài chỉ hỏi phương trình một ẩn.
Câu 3 :
\({x_0}\) được gọi là nghiệm của phương trình \(A\left( x \right) = B\left( x \right)\) nếu:
-
A.
\(A\left( {{x_0}} \right) < B\left( {{x_0}} \right)\)
-
B.
\(A\left( {{x_0}} \right) > B\left( {{x_0}} \right)\)
-
C.
\(A\left( {{x_0}} \right) \ne B\left( {{x_0}} \right)\)
-
D.
\(A\left( {{x_0}} \right) = B\left( {{x_0}} \right)\)
Đáp án : D
Phương pháp giải :Sử dụng khái niệm nghiệm của phương trình: Số \({x_0}\) được gọi là nghiệm của phương trình \(A\left( x \right) = B\left( x \right)\) nếu giá trị của A(x) và B(x) tại \({x_0}\) bằng nhau.Lời giải chi tiết :Số \({x_0}\) được gọi là nghiệm của phương trình \(A\left( x \right) = B\left( x \right)\) nếu giá trị của A(x) và B(x) tại \({x_0}\) bằng nhau. Tức là \(A\left( {{x_0}} \right) = B\left( {{x_0}} \right)\)Câu 4 :
Phương trình dạng \(ax + b = 0\), với a, b là hai số đã cho được gọi là phương trình bậc nhất một ẩn x khi:
-
A.
Với mọi giá trị của a, b
-
B.
\(a \ne 0;b \ne 0\)
-
C.
\(a \ne 0\)
-
D.
\(b \ne 0\)
Đáp án : C
Phương pháp giải :Sử dụng khái niệm phương trình bậc nhất một ẩn: Phương trình dạng \(ax + b = 0\), với a, b là hai số đã cho và \(a \ne 0\) được gọi là phương trình bậc nhất một ẩn x.Lời giải chi tiết :Theo khái niệm về phương trình bậc nhất một ẩn: Phương trình dạng \(ax + b = 0\), với a, b là hai số đã cho và \(a \ne 0\) được gọi là phương trình bậc nhất một ẩn x.Câu 5 :
Cho phương trình \(2x + 1 = 0\), chọn khẳng định đúng
-
A.
Hệ số của x là 2, hạng tử tự do là 1
-
B.
Hệ số của x là 1, hạng tử tự do là 2
-
C.
Hệ số của x là \( - 1,\) hạng tử tự do là 2
-
D.
Hệ số của x là 2, hạng tử tự do là \( - 1\)
Đáp án : A
Phương pháp giải :Phương trình bậc nhất một ẩn (ẩn x) \(ax + b = 0\) (\(a \ne 0\)) có a gọi là hệ số của x, b gọi là hạng tử tự doLời giải chi tiết :Phương trình \(2x + 1 = 0\) có hệ số của x là 2, hạng tử tự do là 1Câu 6 :
Nghiệm của phương trình \(3x - 6 = 0\) là:
-
A.
\(x = \frac{1}{2}\)
-
B.
\(x = \frac{{ - 1}}{2}\)
-
C.
\(x = 2\)
-
D.
\(x = - 2\)
Đáp án : C
Phương pháp giải :Sử dụng cách giải phương trình bậc nhất một ẩn.Lời giải chi tiết :\(3x - 6 = 0\)
\(3x = 0 + 6\)
\(3x = 6\)
\(x = \frac{6}{3} \)
\(x = 2\)
Vậy phương trình có nghiệm \(x = 2\)
Câu 7 :
Nghiệm của phương trình \(\frac{3}{4} + \frac{2}{5}x = 0\) có dạng \(x = - \frac{a}{b},\) trong đó \(b > 0\) và \(\frac{a}{b}\) là phân số tối giản. Khẳng định nào sau đây đúng?
-
A.
\(a + b = 21\)
-
B.
\(a + b = 23\)
-
C.
\(a + b = 20\)
-
D.
\(a + b = 24\)
Đáp án : B
Phương pháp giải :Sử dụng cách giải phương trình bậc nhất một ẩn.Lời giải chi tiết :\(\frac{3}{4} + \frac{2}{5}x = 0\)
\(\frac{2}{5}x = \frac{{ - 3}}{4}\)
\(x = \frac{{ - 3}}{4}:\frac{2}{5} = \frac{{ - 15}}{8}\)
Do đó, \(a = 15,b = 8\)
Vậy \(a + b = 15 + 8 = 23\)
Câu 8 :
Ở một số quốc gia, người ta dùng cả hai đơn vị đo nhiệt độ là Fahrenheit (oF) và độ Celcius (oC), liên hệ với nhau bởi công thức \(C = \frac{5}{9}\left( {F - 32} \right).\) Khi ở 20 oC thì ứng với độ Fahrenheit là:
-
A.
34 oF
-
B.
38 oF
-
C.
64 oF
-
D.
68 oF
Đáp án : D
Phương pháp giải :Sử dụng cách giải phương trình đưa về dạng \(ax + b = 0\).Lời giải chi tiết :Với \(C = {20^o}C\) ta có:
\(20 = \frac{5}{9}\left( {F - 32} \right)\)
\(F - 32 = 20 : \frac{5}{9}\)
\(F - 32 = 36\)
\(F = 36 + 32 = 68\)
Vậy \(C = {20^o}C\) thì ứng với 68 oF
Câu 9 :
Biết rằng \(4x - 8 = 0\). Giá trị của biểu thức \(5{x^2} - 4\) là:
-
A.
\( - 24\)
-
B.
\(24\)
-
C.
\( - 16\)
-
D.
16
Đáp án : D
Phương pháp giải :Sử dụng cách giải phương trình bậc nhất một ẩn.Lời giải chi tiết :\(4x - 8 = 0\)
\(4x = 8\)
\(x = \frac{8}{4} = 2\)
Với \(x = 2\) thay vào biểu thức \(5{x^2} - 4\) ta có: \({5.2^2} - 4 = 16\)
Câu 10 :
Phương trình \({x^2} + 4 = 0\) có bao nhiêu nghiệm?
-
A.
Vô nghiệm
-
B.
Vô số nghiệm
-
C.
1 nghiệm
-
D.
2 nghiệm
Đáp án : A
Phương pháp giải :Sử dụng khái niệm nghiệm của phương trình: Số \({x_0}\) được gọi là nghiệm của phương trình \(A\left( x \right) = B\left( x \right)\) nếu giá trị của A(x) và B(x) tại \({x_0}\) bằng nhau.Lời giải chi tiết :Vì \({x^2} \ge 0\) với mọi x nên \({x^2} + 4 > 0\) với mọi x.
Do đó, phương trình \({x^2} + 4 = 0\) vô nghiệm.
Câu 11 :
Tìm x, biết rằng nếu lấy x trừ đi \(\frac{1}{4},\) rồi nhân kết quả với \(\frac{1}{2}\) thì được \(\frac{1}{8}\)
-
A.
\(x = \frac{1}{2}\)
-
B.
\(x = - \frac{1}{2}\)
-
C.
\(x = \frac{1}{4}\)
-
D.
\(x = \frac{{ - 1}}{4}\)
Đáp án : A
Phương pháp giải :Sử dụng cách giải phương trình đưa về dạng \(ax + b = 0\).Lời giải chi tiết :Theo đề bài ta có: \(\left( {x - \frac{1}{4}} \right).\frac{1}{2} = \frac{1}{8}\)
\(x - \frac{1}{4} = \frac{1}{8}:\frac{1}{2} = \frac{1}{4}\)
\(x = \frac{1}{4} + \frac{1}{4} = \frac{1}{2}\)
Vậy \(x = \frac{1}{2}\)
Câu 12 :
Gọi \({x_0}\) là nghiệm của phương trình \(3\left( {x - 5} \right) + 9x\left( {x - 3} \right) = 9{x^2}.\)
Hãy chọn đáp án đúng.
-
A.
\({x_0}
- B.
\({x_0}- C.
\({x_0} > 0\)- D.
\({x_0} > 1\)Đáp án : A
Phương pháp giải :Sử dụng cách giải phương trình đưa về dạng \(ax + b = 0\).Lời giải chi tiết :\(3\left( {x - 5} \right) + 9x\left( {x - 3} \right) = 9{x^2}\)
\(3x - 15 + 9{x^2} - 27x = 9{x^2}\)
\( - 24x = 15\)
\(x = \frac{{ - 5}}{8}\)
Khi đó, nghiệm của phương là \({x_0} = \frac{{ - 5}}{8}\)
Do đó, \({x_0}
Câu 13 :
Cho \(A = \frac{{2\left( {x + 1} \right)}}{3} - \frac{1}{2},B = \frac{{1 + 3x}}{4}\). Tìm x để \(A = B\)
-
A.
\(x = 1\)
-
B.
\(x = - 1\)
-
C.
\(x = - 2\)
-
D.
\(x = 2\)
Đáp án : B
Phương pháp giải :Sử dụng cách giải phương trình đưa về dạng \(ax + b = 0\).Lời giải chi tiết :Vì \(A = B\) nên \(\frac{{2\left( {x + 1} \right)}}{3} - \frac{1}{2} = \frac{{1 + 3x}}{4}\)
\(\frac{{8\left( {x + 1} \right)}}{{12}} - \frac{6}{{12}} = \frac{{3\left( {1 + 3x} \right)}}{{12}}\)
\(8x + 8 - 6 = 3 + 9x\)
\(9x - 8x = 2 - 3\)
\(x = - 1\)
Câu 14 :
Cho hai phương trình \(8\left( {x - 2} \right) = 14 + 6\left( {x - 1} \right) + 2\left( {x + 5} \right)\,\,\left( 1 \right)\) và \({\left( {x - 2} \right)^2} = {x^2} - 2x - 2\left( {x - 2} \right)\;\;\left( 2 \right)\)
Hãy chọn đáp án đúng.
-
A.
Phương trình (1) vô nghiệm, phương trình (2) có nghiệm duy nhất
-
B.
Phương trình (1) có vô số nghiệm, phương trình (2) vô nghiệm
-
C.
Phương trình (1) vô nghiệm, phương trình (2) có vô số nghiệm
-
D.
Cả phương trình (1) và phương trình (2) đều có một nghiệm
Đáp án : C
Phương pháp giải :Sử dụng cách giải phương trình đưa về dạng \(ax + b = 0\).Lời giải chi tiết :\(8\left( {x - 2} \right) = 14 + 6\left( {x - 1} \right) + 2\left( {x + 5} \right)\,\)
\(8x - 16 = 14 + 6x - 6 + 2x + 10\)
\(8x - 6x - 2x = 18 + 16\)
\(0 = 34\) (vô lí)
Vậy phương trình (1) vô nghiệm.
\({\left( {x - 2} \right)^2} = {x^2} - 2x - 2\left( {x - 2} \right)\)
\({x^2} - 4x + 4 = {x^2} - 2x - 2x + 4\)
\({x^2} - 4x + 4 - {x^2} + 4x - 4 = 0\)
\(0 = 0\) (luôn đúng)
Vậy phương trình (2) có vô số nghiệm.
Câu 15 :
Cho phương trình: \(\frac{{x - 11}}{{2011}} + \frac{{x - 10}}{{2012}} = \frac{{x - 74}}{{1948}} + \frac{{x - 72}}{{1950}}\).
Khẳng định nào sau đây đúng?
-
A.
Nghiệm của phương trình là một chia hết cho 5
-
B.
Nghiệm của phương trình là một số chia hết cho 2
-
C.
Nghiệm của phương trình là một chia hết cho 4
-
D.
Nghiệm của phương trình là một số nguyên tố
Đáp án : B
Phương pháp giải :Sử dụng cách giải phương trình đưa về dạng \(ax + b = 0\): Trừ các phân thức đại số cho 1, các phân thức được biến đổi về cùng tử số x – 2022.Lời giải chi tiết :\(\frac{{x - 11}}{{2011}} + \frac{{x - 10}}{{2012}} = \frac{{x - 74}}{{1948}} + \frac{{x - 72}}{{1950}}\)
\(\left( {\frac{{x - 11}}{{2011}} - 1} \right) + \left( {\frac{{x - 10}}{{2012}} - 1} \right) = \left( {\frac{{x - 74}}{{1948}} - 1} \right) + \left( {\frac{{x - 72}}{{1950}} - 1} \right)\)
\(\frac{{x - 2022}}{{2011}} + \frac{{x - 2022}}{{2012}} - \frac{{x - 2022}}{{1948}} - \frac{{x - 2022}}{{1950}} = 0\)
\(\left( {x - 2022} \right)\left( {\frac{1}{{2011}} + \frac{1}{{2012}} - \frac{1}{{1948}} - \frac{1}{{1950}}} \right) = 0\)
\(x - 2022 = 0\) (vì \(\frac{1}{{2011}} + \frac{1}{{2012}} - \frac{1}{{1948}} - \frac{1}{{1950}} < 0\))
\(x = 2022\)
Vì 2022 chia hết cho 2, không chia hết cho 4, không chia hết cho 5 nên nghiệm của phương trình là một số chia hết cho 2
Câu 16 :
Tìm điều kiện của m để phương trình \(3mx + m - 4x = 3{m^2} + 1\) có nghiệm duy nhất
-
A.
\(m \ne \frac{4}{3}\)
-
B.
\(m = \frac{4}{3}\)
-
C.
\(m = \frac{3}{4}\)
-
D.
\(m \ne \frac{3}{4}\)
Đáp án : A
Phương pháp giải :+ Sử dụng cách giải phương trình đưa về dạng \(ax + b = 0\).
+ Sử dụng khái niệm phương trình bậc nhất một ẩn: Phương trình dạng \(ax + b = 0\), với a, b là hai số đã cho và \(a \ne 0\) được gọi là phương trình bậc nhất một ẩn x.
Lời giải chi tiết :\(3mx + m - 4x = 3{m^2} + 1\)
\(\left( {3m - 4} \right)x + m - 3{m^2} - 1 = 0\)
Để phương trình \(\left( {3m - 4} \right)x + m - 3{m^2} - 1 = 0\) có nghiệm duy nhất thì \(3m - 4 \ne 0\)
\(3m \ne 4\)
\(m \ne \frac{4}{3}\)
Vậy \(m \ne \frac{4}{3}\)
Câu 17 :
Hình tam giác và hình chữ nhật ở hình dưới có cùng chu vi. Khi đó, giá trị của x là:

-
A.
\(x = - 2\)
-
B.
\(x = 2\)
-
C.
\(x = 1\)
-
D.
\(x = - 1\)
Đáp án : C
Phương pháp giải :+ Sử dụng cách giải phương trình đưa về dạng \(ax + b = 0\).
+ Sử dụng chu vi hình tam giác: Chu vi hình tam giác bằng tổng độ dài ba cạnh của tam giác
+ Sử dụng chu vi hình chữ nhật: Chu vi hình tam giác bằng hai lần tổng chiều dài và chiều rộng
Lời giải chi tiết :Chu vi hình tam giác là: \(x + 2 + x + 4 + x + 5 = 3x + 11\)
Chu vi hình chữ nhật là: \(2\left( {x + 1 + x + 4} \right) = 2\left( {2x + 5} \right) = 4x + 10\)
Vì hai hình có chu vi bằng nhau nên: \(3x + 11 = 4x + 10\)
\(4x - 3x = 11 - 10\)
\(x = 1\)
Câu 18 :
Cho hai phương trình \(\frac{{7x}}{8} - 5\left( {x - 9} \right) = \frac{1}{6}\left( {20x + 1,5} \right)\left( 1 \right)\) và \(2\left( {a - 1} \right)x - a\left( {x - 1} \right) = 2a + 3\;\left( 2 \right)\)
Để phương trình (2) có một nghiệm bằng một phần ba nghiệm của phương trình (1) thì giá trị của a là:
-
A.
\(a = 7\)
-
B.
\(a = - 7\)
-
C.
\(a = \frac{1}{7}\)
-
D.
\(a = \frac{{ - 1}}{7}\)
Đáp án : A
Phương pháp giải :+ Sử dụng cách giải phương trình đưa về dạng \(ax + b = 0\).
+ Sử dụng khái niệm nghiệm của phương trình: Số \({x_0}\) được gọi là nghiệm của phương trình \(A\left( x \right) = B\left( x \right)\) nếu giá trị của A(x) và B(x) tại \({x_0}\) bằng nhau.
Lời giải chi tiết :\(\frac{{7x}}{8} - 5\left( {x - 9} \right) = \frac{1}{6}\left( {20x + 1,5} \right)\)
\(\frac{{21x}}{{24}} - \frac{{120\left( {x - 9} \right)}}{{24}} = \frac{{4\left( {20x + 1,5} \right)}}{{24}}\)
\(21x - 120x + 1080 = 80x + 6\)
\( - 179x = - 1074\)
\(x = 6\)
Vì phương trình (2) có một nghiệm bằng một phần ba nghiệm của phương trình (1) nên phương trình (2) có nghiệm là \(x = 2\)
\(2\left( {a - 1} \right)x - a\left( {x - 1} \right) = 2a + 3\;\left( 2 \right)\)
Với \(x = 2\) thay vào phương trình (2) ta có:
\(2\left( {a - 1} \right)2 - a\left( {2 - 1} \right) = 2a + 3\)
\(4a - 4 - a = 2a + 3\)
\(a = 7\)
Câu 19 :
Phương trình \(\frac{{x + 1}}{3} + \frac{{3\left( {2x + 1} \right)}}{4} = \frac{{2x + 3\left( {x + 1} \right)}}{6} + \frac{{7 + 12x}}{{12}}\) có bao nhiêu nghiệm?
-
A.
1 nghiệm
-
B.
2 nghiệm
-
C.
Không có nghiệm nào
-
D.
Có vô số nghiệm
Đáp án : D
Phương pháp giải :Sử dụng cách giải phương trình đưa về dạng \(ax + b = 0\).Lời giải chi tiết :\(\frac{{x + 1}}{3} + \frac{{3\left( {2x + 1} \right)}}{4} = \frac{{2x + 3\left( {x + 1} \right)}}{6} + \frac{{7 + 12x}}{{12}}\)
\(\frac{{4\left( {x + 1} \right)}}{{12}} + \frac{{9\left( {2x + 1} \right)}}{{12}} = \frac{{2\left( {5x + 3} \right)}}{{12}} + \frac{{7 + 12x}}{{12}}\)
\(4x + 4 + 18x + 9 = 10x + 6 + 7 + 12x\)
\(22x + 13 = 22x + 13\)
\(0 = 0\) (luôn đúng)
Vậy phương trình đã cho có vô số nghiệm
Câu 20 :
Cho hình vẽ dưới đây. Biết rằng diện tích của cả hình đó bằng \(168{m^2}.\) Khi đó, giá trị của x (mét) là:

-
A.
11m
-
B.
12m
-
C.
13m
-
D.
14m
Đáp án : B
Phương pháp giải :Sử dụng cách giải phương trình đưa về dạng \(ax + b = 0\).Lời giải chi tiết :Hình bên có gồm hai hình chữ nhật:
+ Hình chữ nhật độ dài 2 kích thước là 12m và x (mét) nên diện tích hình là: \(12x\left( {{m^2}} \right)\)
+ Hình chữ nhật có độ dài 2 kích thước là 6m và 4m nên diện tích hình là: \(4.6 = 24\left( {{m^2}} \right)\)
Mà diện tích của cả hình đó bằng \(168{m^2}\) nên ta có:
\(12x + 24 = 168\)
\(12x = 144\)
\(x = 12\)
Vậy \(x = 12m\)
Câu 21 :
Một xe máy khởi hành từ Hà Nội đi Hải Phòng với vận tốc trung bình 32km/h. Sau đó 1 giờ, một ô tô cũng khởi hành từ Hà Nội đi Hải Phòng, cùng đường với xe máy và với vận tốc trung bình 48km/h. Phương trình biểu thị việc ô tô gặp xe máy sau x giờ, kể từ khi ô tô khởi hành là:
-
A.
\(48 = 32\left( {x - 1} \right)\)
-
B.
\(48x = 32\left( {1 - x} \right)\)
-
C.
\(48x = 32\left( {x - 1} \right)\)
-
D.
\(48x = 32\left( {x + 1} \right)\)
Đáp án : D
Phương pháp giải :Phương trình bậc nhất một ẩnLời giải chi tiết :
Giả sử ô tô gặp xe máy tại C như trên hình.
Gọi x (giờ) (x > 0) là khoảng thời gian chuyển động của ôtô đi từ A đến C.
Ô tô đi với vận tốc 48km/h nên quãng đường AC bằng: 48.x (km) (1)
Vì xe máy đi trước ôtô 1 giờ nên thời gian xe máy đi từ A đến C bằng: x + 1 (h)
Xe máy đi với vận tốc 32km/h nên quãng đường AC bằng: 32(x + 1) (km) (2)
Từ (1) và (2) ta có phương trình: 48x = 32(x + 1).
Vậy phương trình là: 48x = 32(x + 1).
Câu 22 :
Cho phương trình \(\left( {{m^2} - 3m + 2} \right)x = m - 2,\) với m là tham số. Giá trị của m để phương trình có vô số nghiệm là:
-
A.
\(m = 1\)
-
B.
\(m = 2\)
-
C.
\(m \in \left\{ {1;2} \right\}\)
-
D.
\(m = 0\)
Đáp án : B
Phương pháp giải :Sử dụng nghiệm của phương trình bậc nhất một ẩn.Lời giải chi tiết :\(\left( {{m^2} - 3m + 2} \right)x = m - 2\left( * \right)\)
Xét \({m^2} - 3m + 2 = 0\)
\({m^2} - m - 2m + 2 = 0\)
\(\left( {m - 1} \right)\left( {m - 2} \right) = 0\)
Từ đó tính được \(m = 1;m = 2\)
Với \(m = 1\) thay vào (*) ta có: \(0.x = - 1\) (vô lí) nên phương trình (*) vô nghiệm.
Với \(m = 2\) thay vào (*) ta có: \(0x = 0\) (luôn đúng) nên phương trình (*) có vô số nghiệm với mọi số thực x.
Câu 23 :
Số nghiệm của phương trình \(\sqrt x + 1 = 2\sqrt { - x} \) là:
-
A.
1 nghiệm
-
B.
2 nghiệm
-
C.
0 nghiệm
-
D.
Vô số nghiệm
Đáp án : C
Phương pháp giải :Sử dụng khái niệm nghiệm của phương trình: Số \({x_0}\) được gọi là nghiệm của phương trình \(A\left( x \right) = B\left( x \right)\) nếu giá trị của A(x) và B(x) tại \({x_0}\) bằng nhau.Lời giải chi tiết :Khi \(x = 0\) ta có: \(1 = 0\) (vô lí) nên \(x = 0\) không là nghiệm của phương trình đã cho
Khi \(x < 0\) thì \(\sqrt x \) không xác định
Khi \(x > 0\) thì \(\sqrt { - x} \) không xác định
Vậy trong mọi trường hợp, không có giá trị nào thỏa mãn phương trình.
Vậy phương trình đã cho vô nghiệm
Câu 24 :
Hình dưới dây mô tả một đài phun nước. Tốc độ ban đầu của nước là 48 ft/s (ft là một đơn vị đo độ dài với 1ft=0,3048m). Tốc độ v(ft/s) của nước tại thời điểm t(s) được cho bởi công thức \(v = 48 - 30t.\) Thời gian để một giọt nước đi từ mặt đài phun nước đến khi đạt độ cao tối đa là:

-
A.
1,8s
-
B.
1,7s
-
C.
1,6s
-
D.
1,5s
Đáp án : C
Phương pháp giải :Sử dụng cách giải phương trình bậc nhất một ẩn.Lời giải chi tiết :Khi xuất phát từ mặt đài phun nước, giọt nước có \(t = 0.\)
Khi giọt nước đạt độ cao tối đa thì \(v = 0.\) Thay vào công thức ta có:
\(0 = 48 - 30t\)
\(30t = 48\)
\(t = 1,6\)
Vậy thời gian để giọt nước đi từ mặt đài phun nước đến khi đạt độ cao tối đa là: \(1,6 - 0 = 1,6\) (s)
- B.
Trắc nghiệm Bài 2: Giải bài toán bằng cách lập phương trình bậc nhất một ẩn Toán 8 Chân trời sáng tạoLuyện tập và củng cố kiến thức Bài 2: Giải bài toán bằng cách lập phương trình bậc nhất một ẩn Toán 8 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Xem chi tiết
- B.
- Trắc nghiệm Bài 2: Xác suất lí thuyết và xác suất thực nghiệm Toán 8 Chân trời sáng tạo
- Trắc nghiệm Bài 1: Mô tả xác suất bằng tỉ số Toán 8 Chân trời sáng tạo
- Trắc nghiệm Bài 4: Hai hình đồng dạng Toán 8 Chân trời sáng tạo
- Trắc nghiệm Bài 3: Các trường hợp đồng dạng của hai tam giác vuông Toán 8 Chân trời sáng tạo
- Trắc nghiệm Bài 2: Các trường hợp đồng dạng của hai tam giác Toán 8 Chân trời sáng tạo

