Có lẽ khái niệm hình tròn đã quá quen thuộc với chúng ta. Trong bài học này, chúng ta sẽ ôn lại khái niệm hình tròn và định nghĩa rõ về tâm đối xứng của hình tròn, cũng như trả lời được câu hỏi: “Hình tròn có bao nhiêu tâm đối xứng?”.
1. Nhắc lại về đường tròn
Đường tròn: Đường tròn tâm O, bán kính R là tập hợp tất cả những điểm cách O một khoảng R.
Ký hiệu: Đường tròn tâm O, bán kính R được ký hiệu như sau: (O;R) hoặc (O).
Các vị trí tương đối giữa đường tròn và một điểm M bất kỳ:
– Khi điểm M nằm trên đường tròn ta được: OM=R.
– Khi điểm M nằm ngoài đường tròn ta được: OM>R.
– Khi điểm M nằm trong đường tròn ta được: OM<R.
Cùng xem một số ví dụ về đường tròn, cũng như các vị trí tương đối giữa đường tròn và một điểm bất kỳ.
Ví dụ 1:
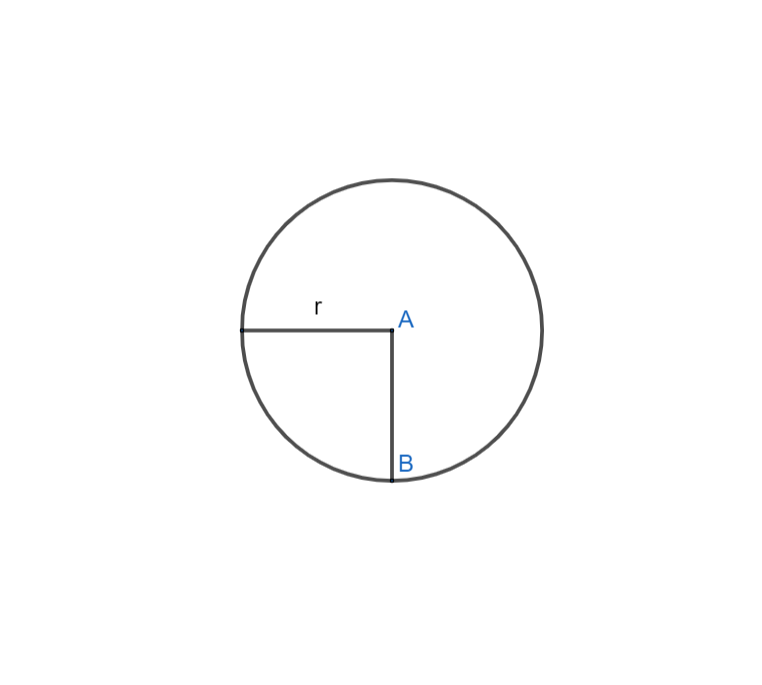
Hình trên biểu diễn đường tròn tâm A, bán kính r. Ký hiệu: (A;r) hoặc (A). Điểm B nằm trên đường tròn nên ta được: AB=r.
Ví dụ 2:
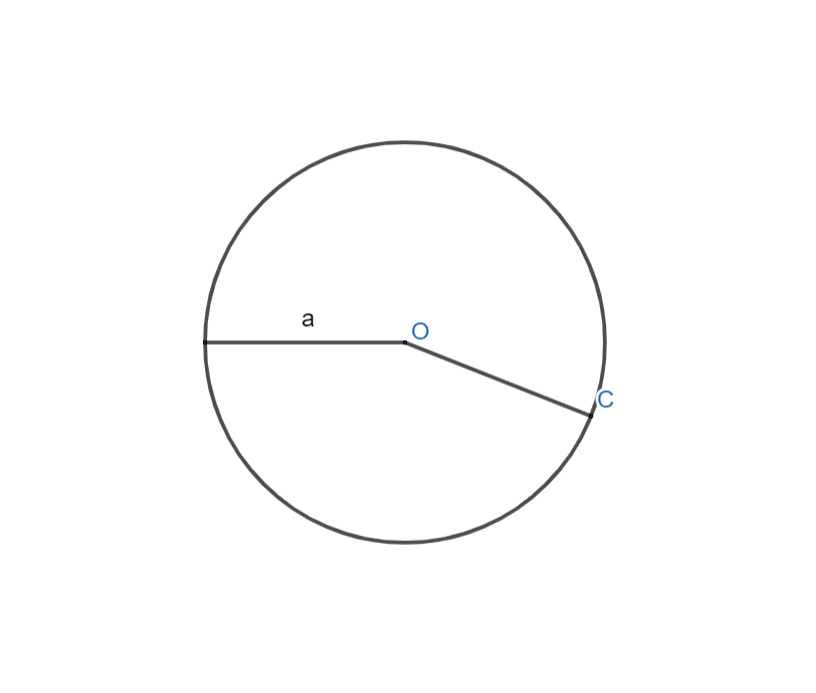
Hình trên biểu diễn đường tròn tâm O, bán kính a. Ký hiệu: (O;a) hoặc (O). Điểm C nằm trên đường tròn nên ta được: OC=a.
Ví dụ 3:
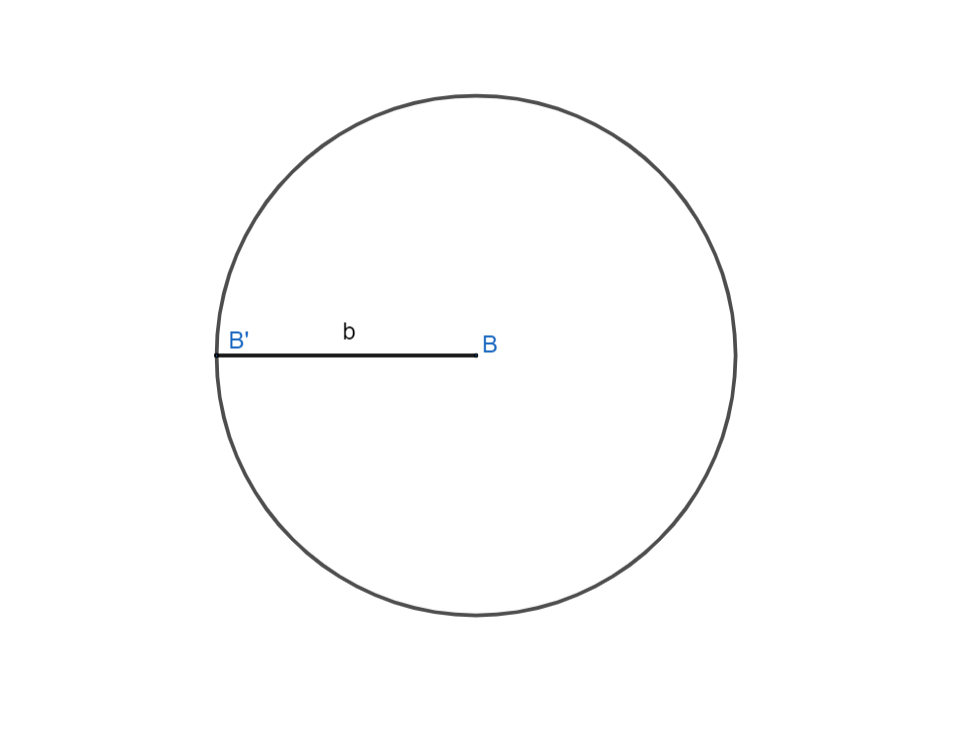
Hình trên biểu diễn đường tròn tâm B, bán kính b. Ký hiệu: (B;b) hoặc (B). Điểm B’ nằm trên đường tròn nên ta được: BB’=b.
Ví dụ 4:
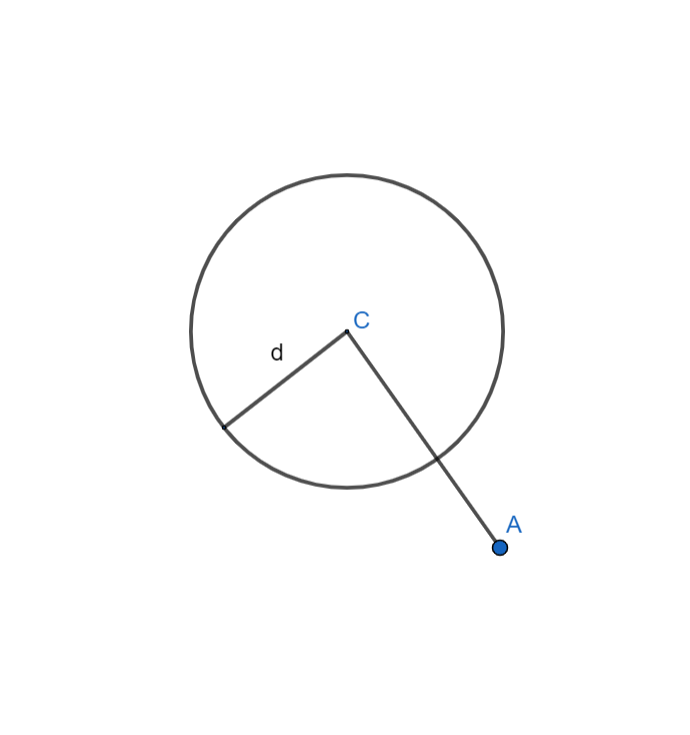
Hình trên biểu diễn đường tròn tâm C, bán kính d. Ký hiệu: (C,d) hoặc (C). Điểm A nằm ngoài đường tròn nên ta được: AC>d.
Ví dụ 5:
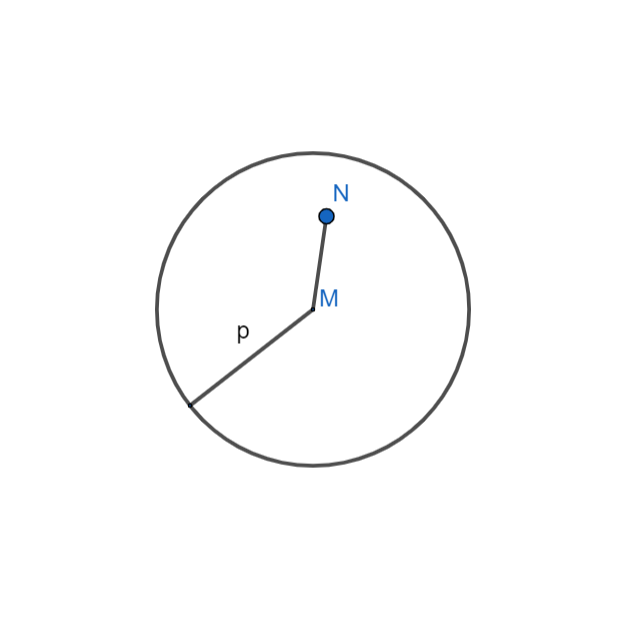
Hình trên biểu diễn đường tròn tâm M, bán kính p. Ký hiệu: (M,p) hoặc (M). Điểm N nằm trong đường tròn nên ta được: MN<p.
2. Tâm đối xứng của đường tròn
Hình tròn là một trong những hình có tâm đối xứng. Vậy tâm đối xứng của hình tròn là gì?
Khái niệm tâm đối xứng của đường tròn:Tâm đối xứng của đường tròn chính là tâm của đường tròn đó.
Ta có thể chứng minh tâm đường tròn chính là tâm đối xứng của đường tròn đó như sau.
Giả thiết: Đường tròn tâm O, bán kính r. Đoạn thẳng AA’ đi qua O sao cho A và A’ nằm trên đường tròn.
Kết luận: A’ đối xứng với A qua O.
Ta chứng minh như sau:
Vì A nằm trên đường tròn nên ta có OA = r.
Vì A’ nằm trên đường tròn nên ta có OA’ = r.
Ta được: OA = OA’, suy ra O là trung điểm của AA’.
Suy ra O là tâm đối xứng của đường thẳng AA’.
Tương tự với vô số điểm A còn lại trên đường tròn, khi kẻ từ điểm A một đường thẳng đi qua tâm O, ta dễ dàng tìm được điểm A’ đối xứng với điểm đó. Vậy có thể nói, tâm đường tròn chính là tâm đối xứng của đường tròn đó.
Chúng ta cùng xem một số ví dụ về tâm đối xứng của đường tròn.
Ví dụ 1:
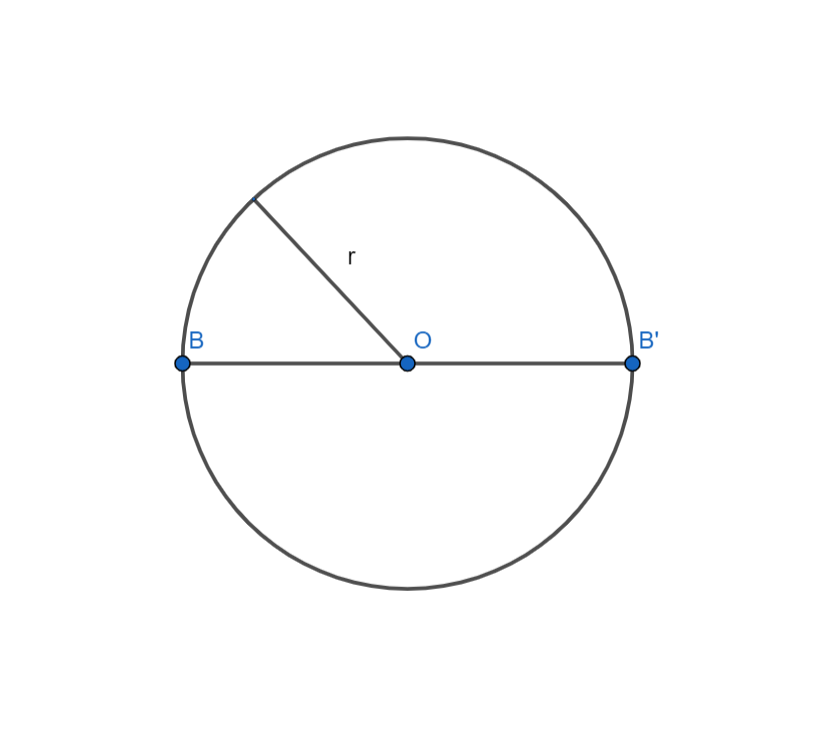
Đường tròn tâm O, bán kính r. Ký hiệu: (O,r) hoặc (O). Tâm O cũng là tâm đối xứng của đường tròn.
Điểm B đối xứng với điểm B’ qua tâm đối xứng O.
Ví dụ 2:
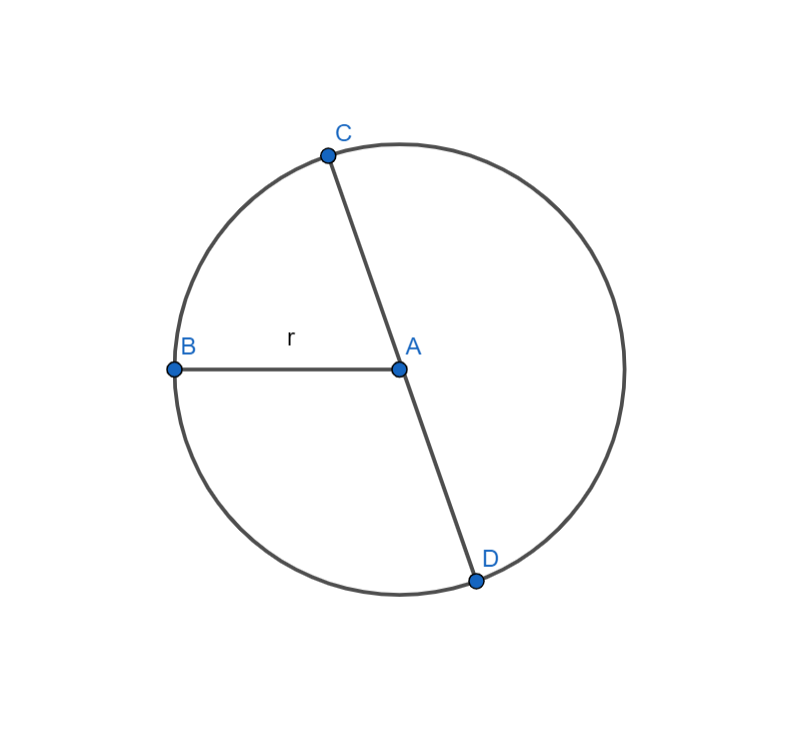
Đường tròn tâm A, bán kính r. Ký hiệu: (A,r) hoặc (A). Tâm A cũng là tâm đối xứng của đường tròn.
Điểm C đối xứng với điểm D qua tâm đối xứng A.
Ví dụ 3:
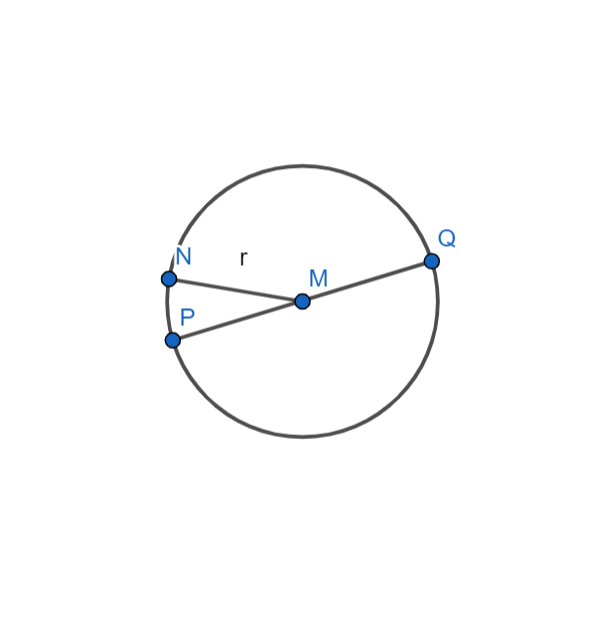
Đường tròn tâm M, bán kính r. Ký hiệu: (M,r) hoặc (M). Tâm M cũng là tâm đối xứng của đường tròn.
Điểm P đối xứng với điểm Q qua tâm đối xứng M.
Ví dụ 4:
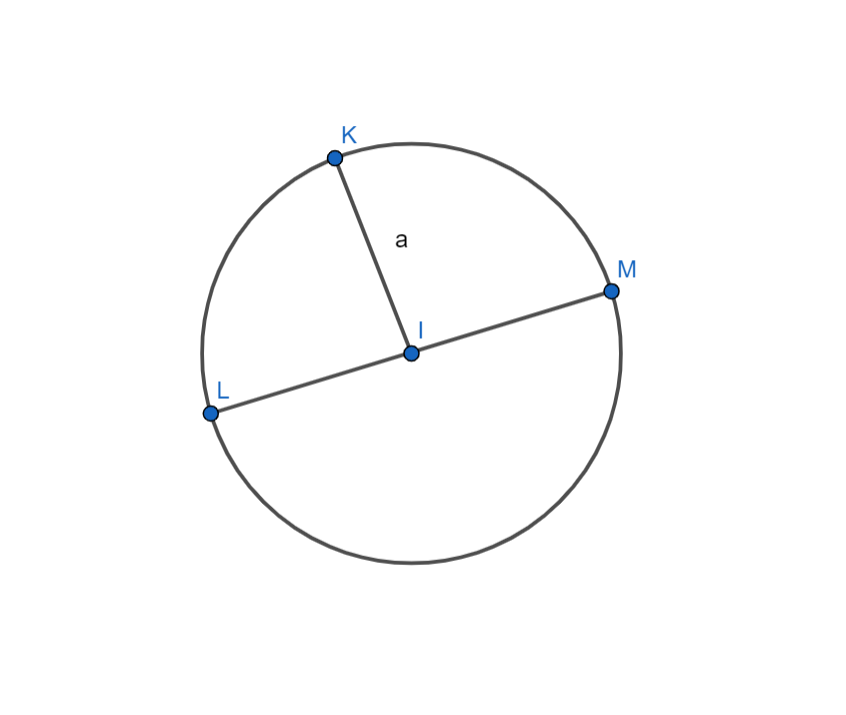
Đường tròn tâm I, bán kính a. Ký hiệu: (I,a) hoặc (I). Tâm I cũng là tâm đối xứng của đường tròn.
Điểm L đối xứng với điểm M qua tâm đối xứng I.
Ví dụ 5:
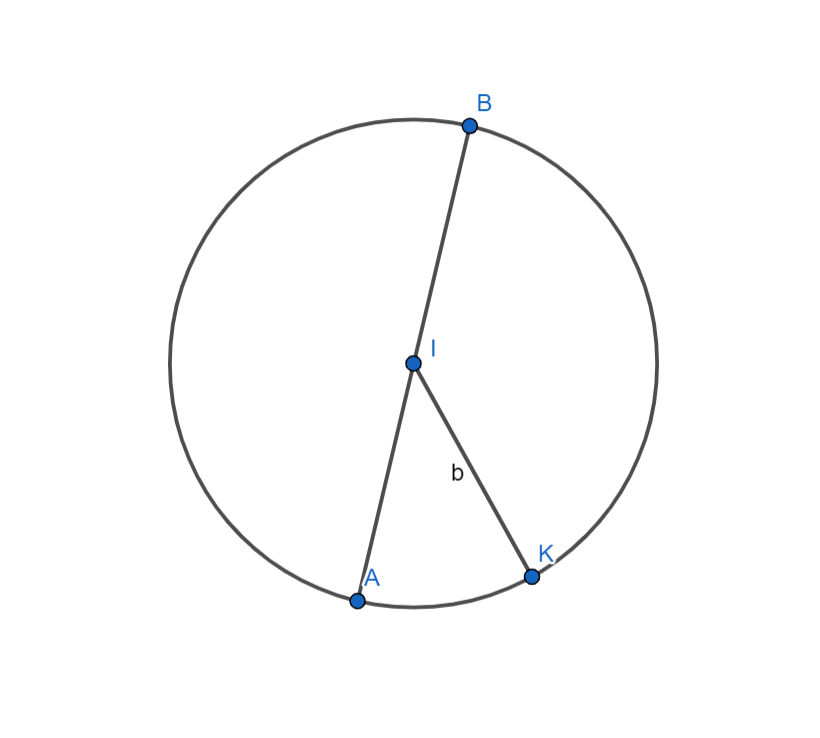
Đường tròn tâm I, bán kính b. Ký hiệu: (I,b) hoặc (I). Tâm I cũng là tâm đối xứng của đường tròn.
Điểm A đối xứng với điểm B qua tâm đối xứng I.
3. Bài tập về tâm đối xứng của đường tròn
Bài 1: Các mệnh đề sau đây đúng hay sai? Tại sao? Nếu sai hãy sửa lại cho đúng
a. Đường tròn là một đường thẳng có tâm và bán kính
b. Đường tròn có một và chỉ một tâm đối xứng
c. Tâm của đường tròn chính là tâm đối xứng của đường tròn đó
d. Cho một điểm bất kỳ nằm ngoài đường tròn, khoảng cách từ điểm đó đến tâm đường tròn bé hơn bán kính của đường tròn đó
e. Cho một điểm bất kỳ nằm trên đường tròn, khoảng cách từ điểm đó đến tâm đường tròn bằng với bán kính của đường tròn đó
f. Có vô số điểm đối xứng nhau qua tâm của đường tròn
ĐÁP ÁN
a.
Sai. Theo khái niệm đường tròn, đường tròn là tập hợp các điểm cách tâm một khoảng nhất định. Đường tròn không phải đường thẳng.
b.
Đúng. Theo như đã nêu ở phần khái niệm tâm đối xứng của đường tròn thì đường tròn chỉ có một tâm đối xứng là tâm đường tròn.
c.
Đúng. Theo như đã nêu ở phần khái niệm tâm đối xứng của đường tròn thì tâm của đường tròn chính là tâm đối xứng của đường tròn đó.
d.
Sai. Khoảng cách từ tâm đường tròn đến một điểm bất kỳ nằm ngoài đường tròn lớn hơn bán kính đường tròn.
e.
Đúng. Vì tâm đường tròn là tâm đối xứng nên ta tìm được vô số điểm đối xứng nhau qua tâm đường tròn.
Bài 2: Trong các hình sau, hình nào có tâm đối xứng
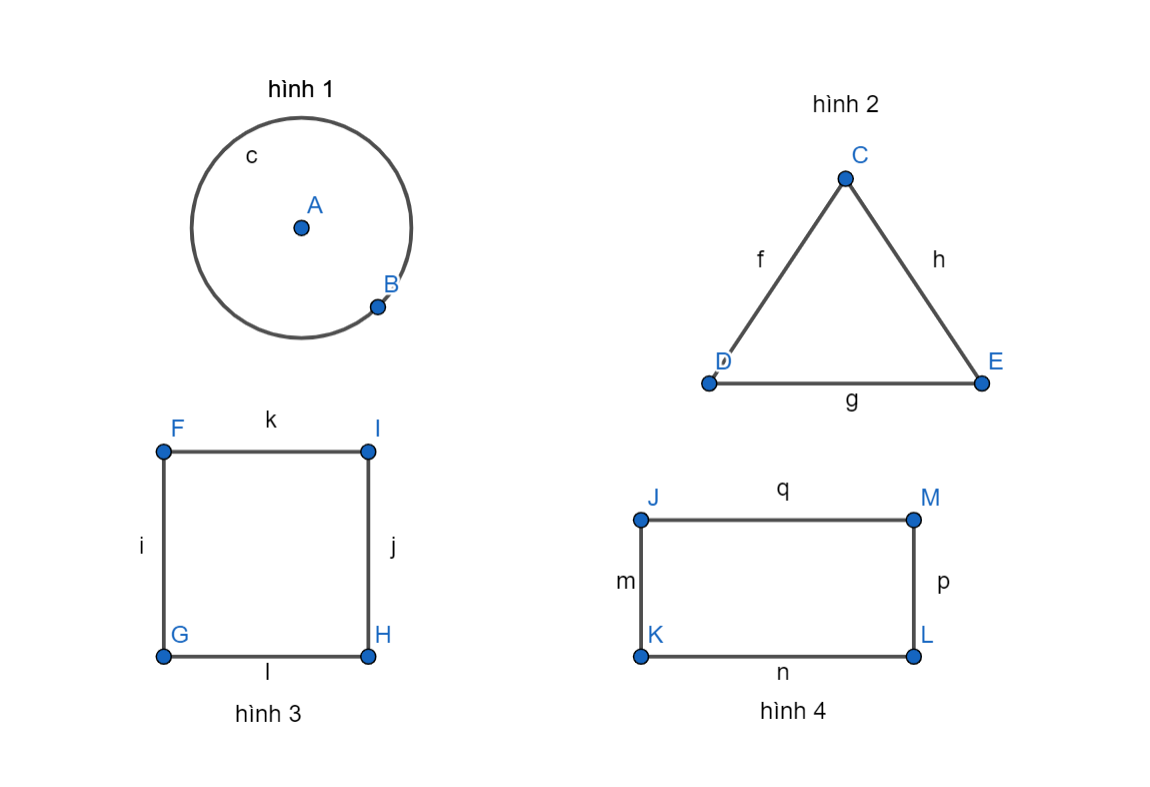
ĐÁP ÁN
Hình 2, hình 3 và hình 4 là hình có tâm đối xứng.
Bài 3: Cho đường tròn tâm O, bán kính r. Có B đối xứng tâm với C qua O. Cho điểm A bất kỳ nằm trên đường tròn. Chứng minh tam giác ABC vuông tại A.
ĐÁP ÁN
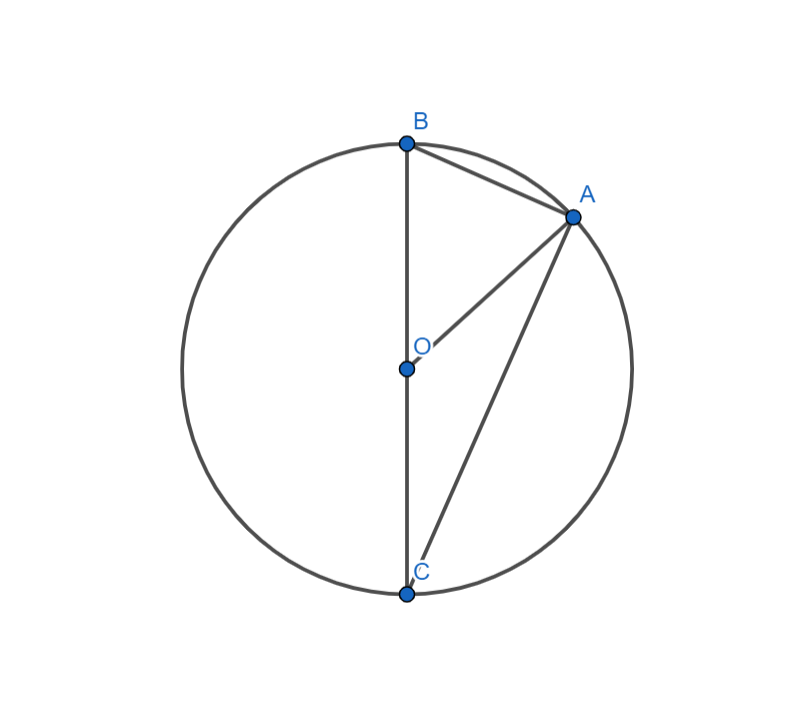
Từ A kẻ đường thẳng AO. Vì A nằm trên đường tròn nên ta có: OA = r
Ta có B đối xứng tâm với C qua O nên:
Từ (1) và (2) ta được
Lại có O là trung điểm của BC nên AO là đường trung tuyến ứng với BC.
Suy ra AO là đường trung tuyến ứng với BC và bằng một nửa BC.
Theo tính chất đường trung tuyến trong tam giác vuông: Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền.
Suy ra ABC là tam giác vuông tại A.
Bài 4: Cho hình vuông bất kỳ, chứng minh bốn điểm của hình vuông cùng thuộc một đường tròn. Đồng thời chỉ ra tâm của đường tròn đó.
ĐÁP ÁN
Ta có hình vuông ABCD, chứng minh bốn điểm A, B, C, D cùng thuộc đường tròn.
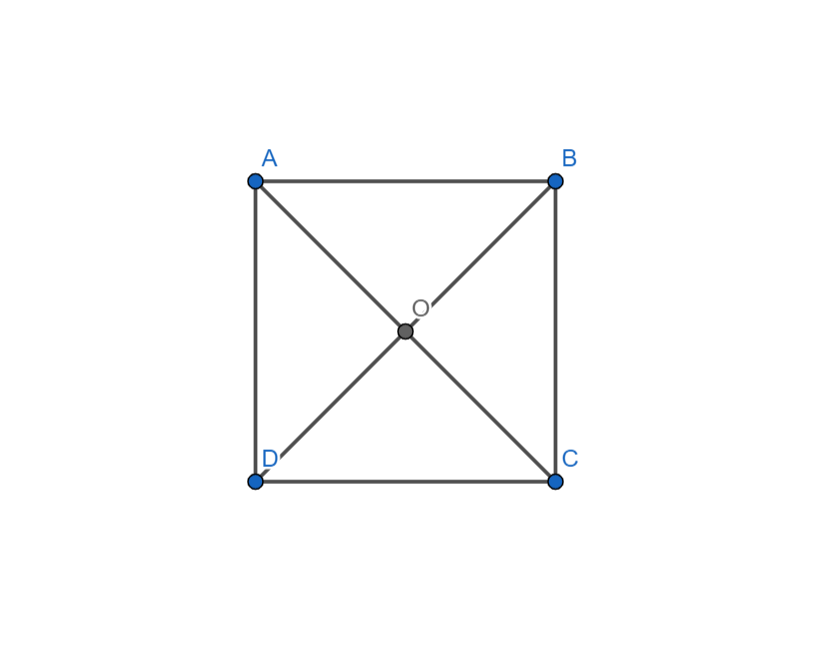
Vì ABCD là hình vuông nên ta có:
(tính chất đường chéo hình vuông)
Suy ra O là tâm đường tròn, bán kính .
Vậy bốn điểm A, B, C, D nằm trên cùng một đường tròn.
Bài 5: Tính bán kính đường tròn trong bài 4, biết rằng cạnh hình vuông có độ dài là 2cm.
ĐÁP ÁN
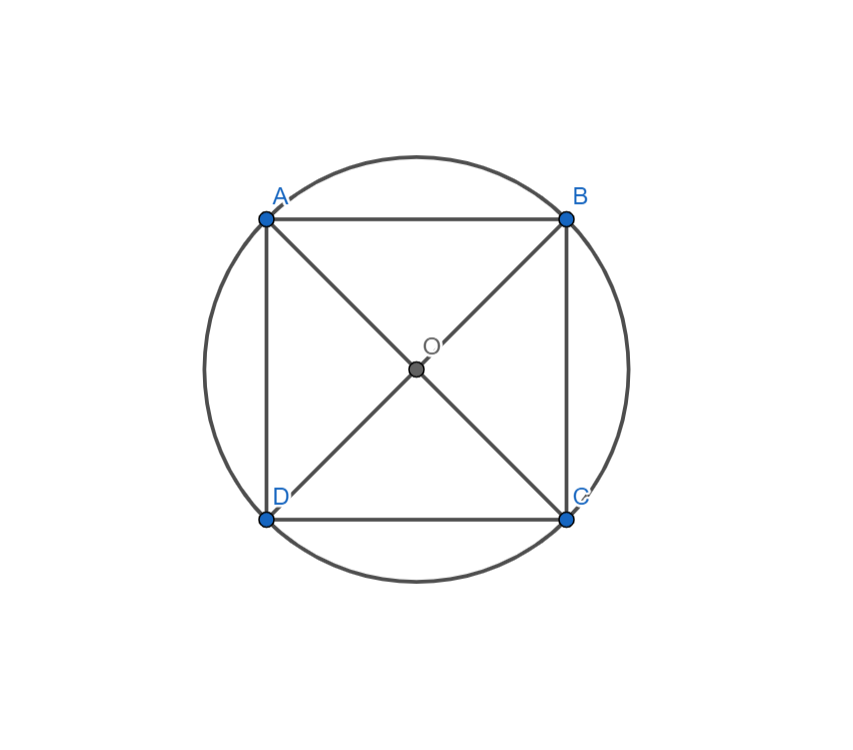
Theo định lý Py-ta-go, ta có:
Lại có:
Vậy bán kính đường tròn là
Vậy là qua bài viết này, các bạn học sinh đã biết được hình tròn có tâm đối xứng không. Hy vọng bài học hôm nay sẽ cung cấp đủ kiến thức để các bạn học tốt các bài học tiếp theo!
Chịu trách nhiệm nội dung: GV Nguyễn Thị Trang

