Những kiến thức về đạo hàm là phần khá quan trọng trong chương trình kiến thức toán lớp 11 trung học phổ thông. Tài Liệu Học Tập đã giúp các bạn tổng hợp tất cả các công thức đạo hàm cơ bản, đạo hàm cao cấp, quy tắc đạo hàm, đạo hàm lượng giác, bảng công thức đạo hàm và cả nguyên hàm để tiện cho việc ôn tập. Ngoài ra, bài viết cũng giới thiệu 8 dạng bài tập đạo hàm thường gặp. Cùng ôn tập lại nhé!
1. Vậy đạo hàm là gì?
1.1 Định nghĩa đạo hàm
Giới hạn, của tỉ số giữa số gia của hàm số và số gia của đối số tại x0, khi số gia của đối số tiến dần tới số 0 thì đó được xem là đạo hàm của hàm y = f(x) tại x0.
Ký hiệu của đạo hàm của hàm số y=f(x) được viết là y′(x0) hoặc f′(x0):
- Số gia của đối số là Δx=x−x0
- Số gia của hàm số là Δy=y−y0
2 – Những quy tắc cơ bản:
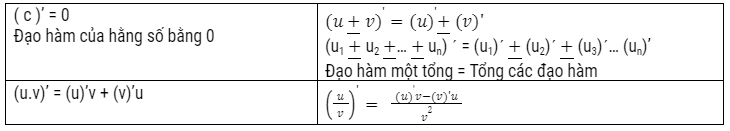
Quy tắc đạo hàm hàm hợp:
2. Tổng hợp những công thức đạo hàm:
2.1. Công thức đạo hàm cơ bản
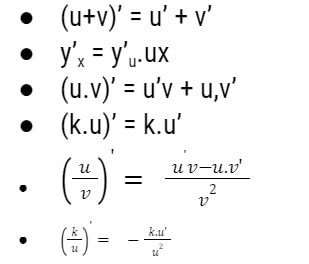
2.2. Công thức đạo hàm hàm sơ cấp
Một số phân thức hữu tỉ thường gặp và đạo hàm của nó:
2.3. Các công thức đạo hàm cấp cao
Định nghĩa đạo hàm cấp cao
Giả sử hàm số y = f(x) có đạo hàm f'(x)
Đạo hàm của hàm số f'(x), nếu có, được gọi là đạo hàm cấp hai của hàm số f(x), kí hiệu là y” hay f”(x).
Đạo hàm của hàm số f”(x), nếu có, được gọi là đạo hàm cấp ba của hàm số f(x), kí hiệu là y”’ hay f”'(x).
Tương tự, đạo hàm của đạo hàm cấp (n-1) được gọi là đạo hàm cấp n của hàm số y = f(x), kí hiệu là y(n) hay f(n)(x).
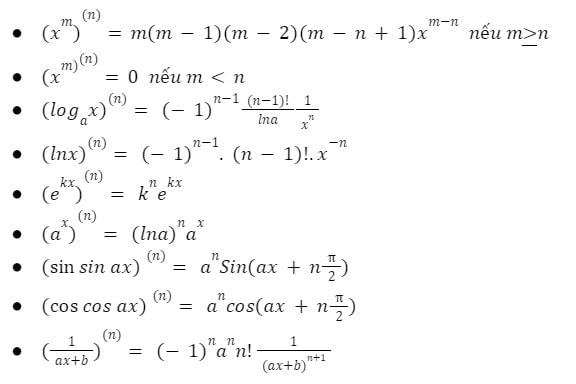
2.4. Công thức đạo hàm hàm lượng giác
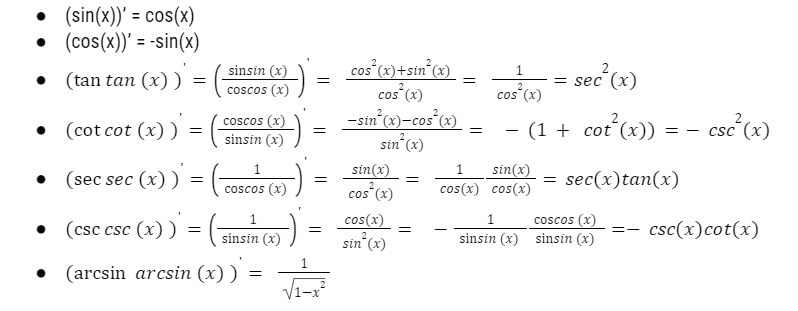
3. Bảng công thức đạo hàm
Bảng tổng hợp công thức đạo hàm dưới đây sẽ giúp bạn ghi nhớ nhanh hơn những kiến thức của chuyên đề này.
4. 8 dạng bài toán liên quan đến công thức đạo hàm
Dạng bài 1: Dùng định nghĩa để tính đạo hàm
Dùng định nghĩa để giải là một trong những bài toán đạo hàm cơ bản nhất trong giải tích. Để giải bài toán này các bạn chỉ cần dựa vào chính định nghĩa của nó để áp dụng và tính toán làm bài một cách chính xác. Hướng làm bài cụ thể như sau:
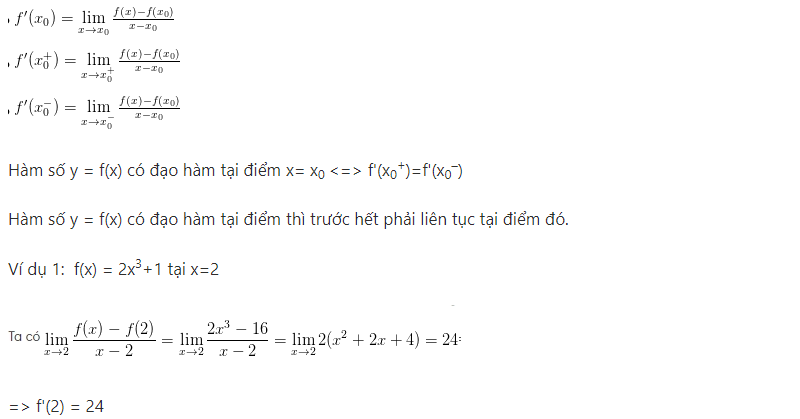
Dạng bài 2: Chứng minh các đẳng thức liên quan đạo hàm
Ở dạng này, đề bài thường sẽ đưa cho bạn một hay hai điều kiện có sẵn và yêu cầu bạn chứng minh một hệ thức, phương trình nào đó. Bạn cần huy động những công thức đạo hàm mình được học để áp dụng biến đổi vào bài toán sao cho ra được hệ thức cần chứng minh. Dạng này có nhiều cấp độ từ dễ đến trung bình và khó.
Dưới đây là một bài tập ví dụ vủa dạng này mức đơn giản.
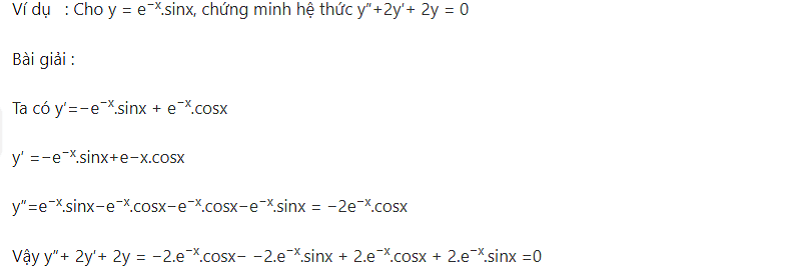
Dạng bài 3: Viết phương trình tiếp tuyến khi biết tiếp điểm
Đây là một trong những dạng giải bài tập khá phổ biến.
Dạng này thường là sẽ cho một phương trình tiếp tuyến của hàm số trên đồ thị của đường cong (C): y= f(x) tại tiếp điểm M( x0 ; y0) và có dạng: y = y’(x0)(x-x0) + y0.
Bài tập ví dụ: Cho một hàm số y= x3 + 3mx2 + ( m+1)x + 1 (1), m là một tham số thực. Hãy tìm các giá trị của m để tiếp tuyến của đồ thị của hàm số tại điểm có hoành độ x = -1 và đi qua điểm A( 1;2).
Hướng dẫn giải:
Tập xác định: D = R
y’ = f'(x)= 3×2 + 6mx + m + 1
Với x0 = -1 => y0= 2m -1, f'( -1) = -5m + 4
Phương trình tiếp tuyến tại M( -1; 2m – 1) : y= ( -5m + 4 ) ( x+1) + 2m -1 (d)
Ta có A ( 1;2) ∈ (d) <=> ( -5m + 4).2 + 2m – 1 = 2 => m = 5/8
Dạng bài 4: Cho biết hệ số góc và từ đó viết phương trình tiếp tuyến
Đề sẽ có dạng: Yêu cầu viết phương trình tiếp tuyến Δ của ( C ) : y = f( x ), biết Δ có hệ số góc là k cho trước
Cách giải:
Gọi M( x0 ; y0) là tiếp điểm. Tính y’ => y'(x0)
Phương trình tiếp tuyến Δ có hệ số góc k => y’ = ( x0 ) = k (i)
- x0 => y0 = f(x0) => Δ : y = k (x – x0 )+ y0
Lưu ý: Hệ số góc k = y'( x0 ) của tiếp tuyến Δ thường cho kiểu gián tiếp như sau:
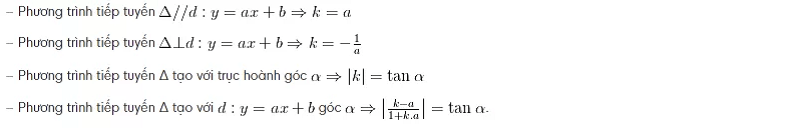Bài tập ví dụ: Cho hàm số y=x3+3×2-9x+5 ( C). Tìm tiếp tuyến có hệ số góc nhỏ nhất trong tất cả các tiếp tuyến của đồ thị ( C ).
Hướng dẫn giải:
Ta có y’ = f'( x ) = 3×2 + 6x – 9
Gọi x0 là hoành độ tiếp điểm của tiếp tuyến, vậy f'( x0) = 3 x02 + 6 x0 – 9
Ta có 3 x02 + 6×0– 9 =3 ( x02+ 2×0 +1) – 12 = 3 (x0+1)2– 12 > – 12
Vậy min f( x0)= – 12 tại x0= -1 => y0=16
Suy ra phương trình tiếp tuyến cần tìm: y= -12( x+1)+16 <=> y= -12x + 4
Dạng bài 5: Bất phương trình và phương trình có đạo hàm
Để giải bài tập của dạng toán này bạn cần kết hợp nhiều công thức với nhau để giải phương trình hoặc một bất phương trình được đề đưa ra và sau đó tính toán ra kết quả cuối cùng.
Dạng bài 6: Dùng công thức tính đạo hàm
Để có thể giải quyết được những bài tập đạng này chính xác, các bạn cần phải thuộc và hiểu được những công thức tính đạo hàm cơ bản. Nếu bạn gặp những hàm số phức tạp thì có thể linh hoạt rút gọn trước hàm số đó rồi mới tiến hành tính đạo hàm. Đặc biệt nhất là thuộc hàm lượng giác nhé.
Bài tập mẫu:
Dạng bài 7: Phương trình tiếp tuyến tại một điểm cho trước thuộc đồ thị/có hệ số góc cho trước của đồ thị hàm số
Dạng này thường xuất hiện trong đề thi THPT quốc gia. Để giải dạng này, các bạn cần nắm vững hai dạng viết phương trình tiếp tuyến cơ bản như sau đây:
Bài tập mẫu:
Dạng bài 8: Bài tập tính đạo hàm cấp cao
Đạo hàm cấp cao thường có các dạng bài tập thiên về tính đạo hàm cấp 2 trở lên, khi đó các bạn có thể áp dụng công thức y(n) = ( y(n-1) )’.
Khó hơn là với trường hợp để tính đạo hàm cấp n, các bạn sẽ phải tính đạo hàm từ cấp 1, 2, 3,…. rồi từ đó mới tìm ra được công thức đạo hàm cấp n. Ngoài ra bạn có thể áp dụng phương pháp quy nạp trong toán học để có thể chứng minh được công thức đó là đúng.
Mọi người có thể tải file PDF tại đây.
Tổng kết
Vậy là bài viết đã giúp cô đọng lại toàn bộ kiến thức về công thức đạo hàm. Các bạn học sinh nên đọc và tham khảo để có được kiến thức tổng quan nhất. Và quan trọng là hãy thường xuyên luyện giải đề về dạng toán này để phát triển tư duy và ghi nhớ các công thức một cách tự nhiên.
Discussion about this post