Lũy thừa là một khái niệm cơ bản nhưng lại có vai trò quan trọng trong nhiều lĩnh vực của toán học. Từ số học đến đại số, từ hình học đến hàm số lượng giác, lũy thừa đều góp mặt và trở thành một thách thức cho học sinh. Nhằm giúp các em nắm rõ các kiến thức lũy thừa và vận dụng giải bài tập hiệu quả, Trường Việt Anh sẽ tổng hợp các công thức lũy thừa chi tiết và đầy đủ nhất để học sinh dễ dàng ghi nhớ và áp dụng.
Định nghĩa lũy thừa
Trước khi tìm hiểu các công thức của lũy thừa, các em cần ôn lại kiến thức lũy thừa là gì, chúng có tính chất và phân loại như thế nào.
Khái niệm
Theo lý thuyết lũy thừa, lũy thừa là một phép toán hai ngôi trong toán học, được thực hiện trên hai số a và n. Kết quả của phép toán này là tích của n thừa số a nhân với nhau.
Ký hiệu lũy thừa được biểu diễn dưới dạng ( a^n ).

Các loại luỹ thừa phát triển từ công thức lũy thừa cơ bản
Có 3 dạng lũy thừa phát triển từ các công thức mũ lũy thừa cơ bản. Bao gồm:
Dạng 1: Lũy thừa số mũ nguyên
Giả sử n là một số nguyên dương và a là một số thực bất kỳ. Lũy thừa bậc n của a là tích của n với thừa số a. Định nghĩa này tương đồng với khái niệm tổng quát, được thể hiện như sau:

Dạng 2: Lũy thừa số mũ hữu tỉ

Dạng 3: Lũy thừa số mũ vô tỉ
Cho (a>0) và (alphainmathbb{R}) là một số vô tỉ, khi đó ( a^{alpha} = overset{lim}{underset{n to +infty}{rule{1.5cm}{0.4pt}}} ; a^{,r_n} ) với ({r_n}) là dãy số hữu tỉ thỏa mãn (lim_{nto +infty} r_n=alpha).
Tính chất của lũy thừa số mũ thực
- (a^{x}cdot a^{y}=a^{,x+y})
- (a^{x}:a^{y}=a^{,x-y})
- ((a^x)^y = a^{xy})
- ((ab)^{x}=a^{x}b^{x})
- (left(frac{a}{b}right)^{x}=frac{a^{x}}{b^{x}})
- (a^{x}>0, forall xinmathbb{R})
- (a^{x}=a^{y} Leftrightarrow x=y (aneq 1))
- Với (a>1) thì (a^{x}>a^{y} Leftrightarrow x>y); với (0<a<1) thì (a^{x}>a^{y} Leftrightarrow x<y).
- Với (0<a<b): nếu (m) là số nguyên dương thì (a^{m}<b^{m}); nếu (m) là số nguyên âm thì (a^{m}>b^{m}).
Tính chất của luỹ thừa
Ta có thể xét lũy thừa theo ba tính chất sau đây:
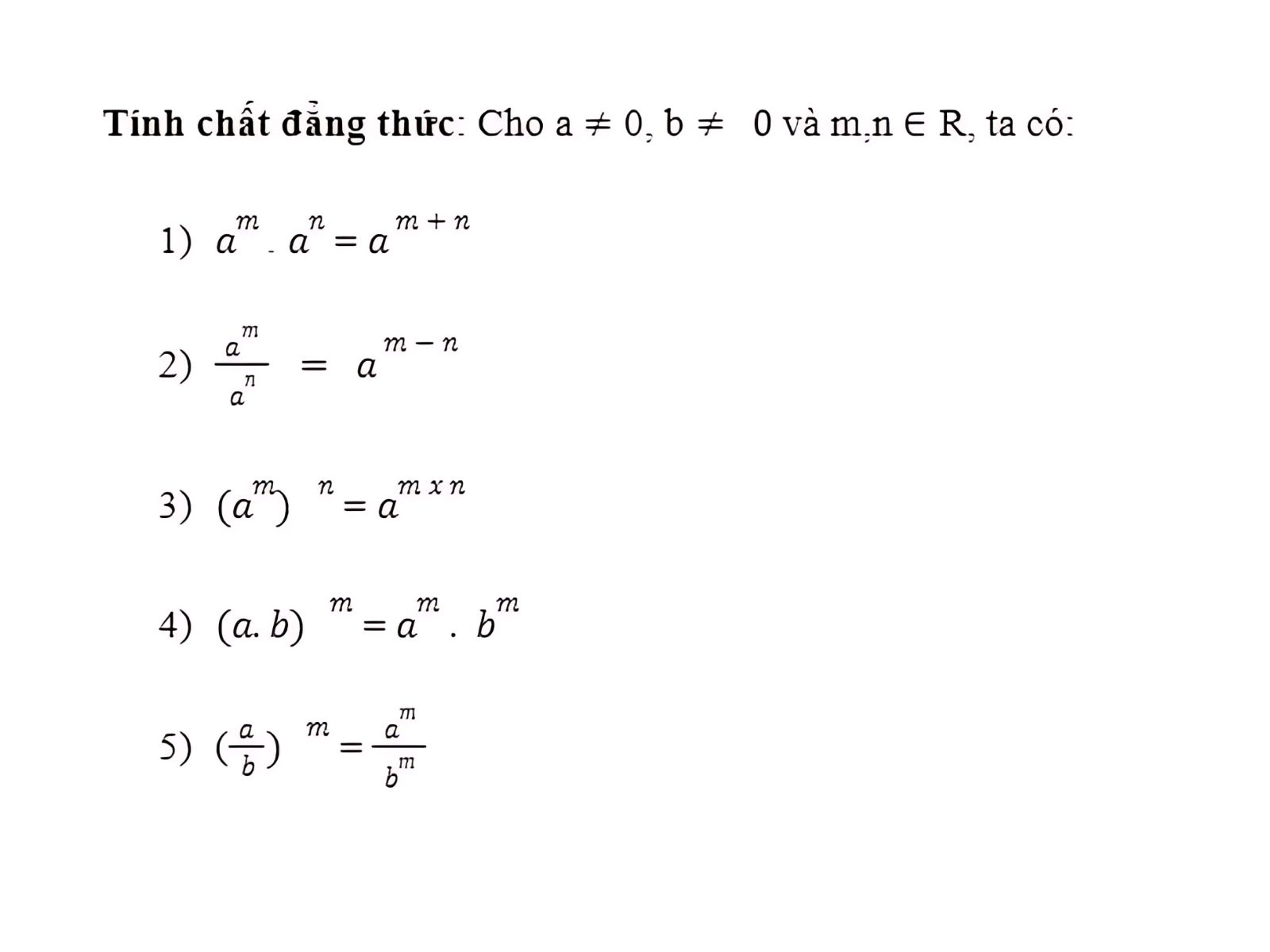

Tổng hợp công thức lũy thừa toán 12
Dưới đây là bảng công thức từ căn bản đến các trường hợp đặc biệt mà các em học sinh cần nắm rõ:



Có thể bạn quan tâm:
- Tổng hợp các định lý toán học (THCS- THPT) cần biết
- Ký hiệu trong toán học và ý nghĩa các ký hiệu trong toán học
Các dạng bài tập áp dụng công thức lũy thừa
Để hiểu hơn các công thức toán 12 về lũy thừa, các em có thể tham khảo một số dạng bài tập kèm lời giải chi tiết sau:
Tính giá trị biểu thức
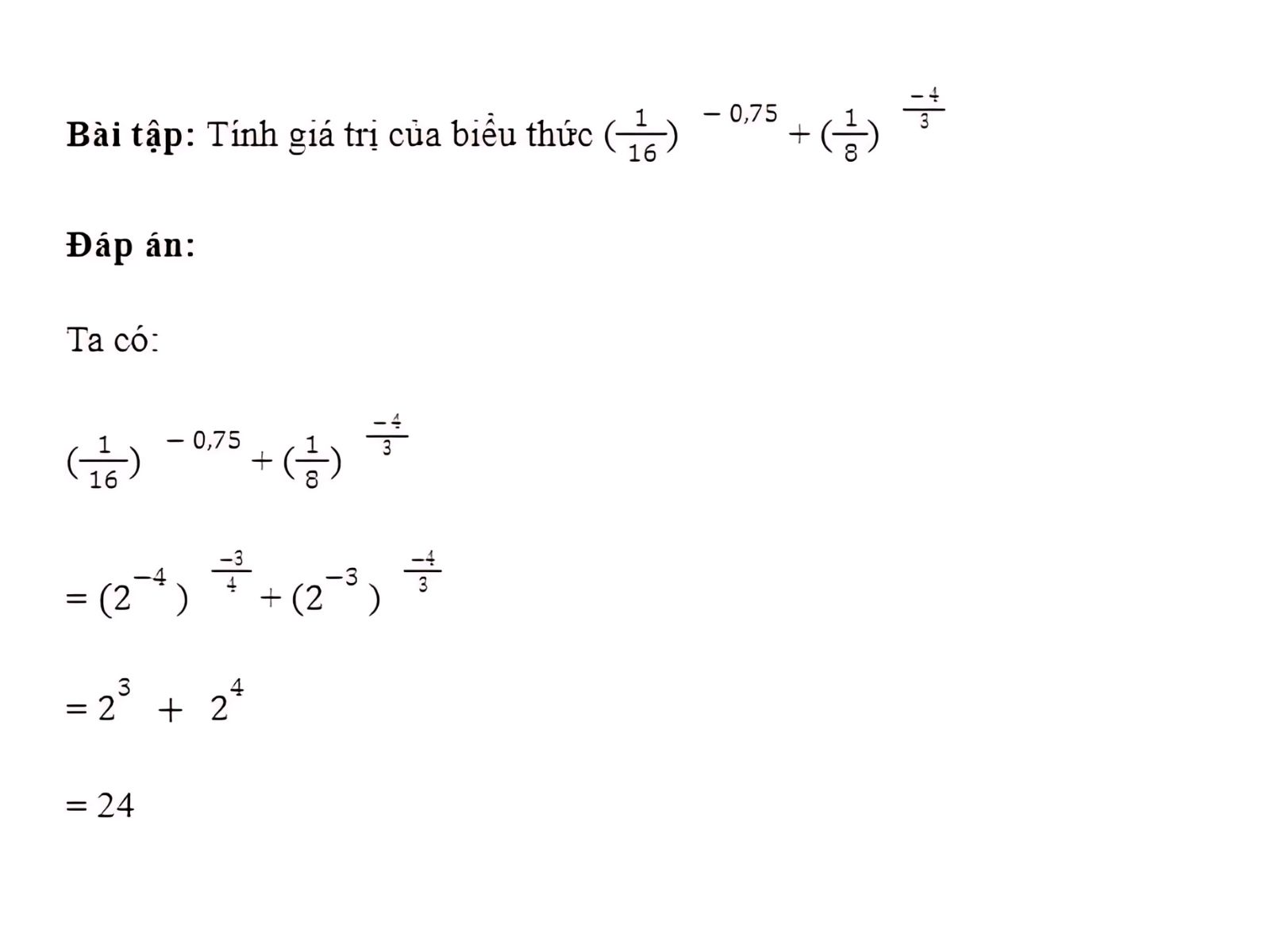
Rút gọn biểu thức
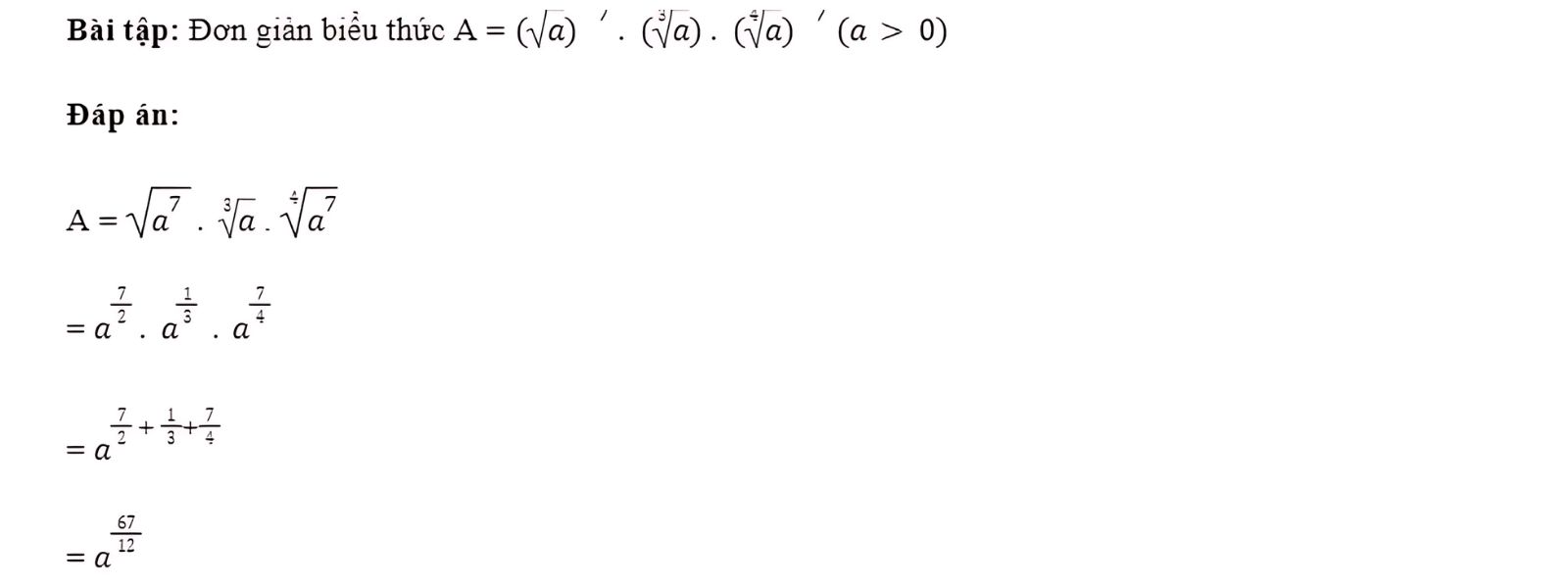
Giải phương trình chứa lũy thừa


Chứng minh đẳng thức
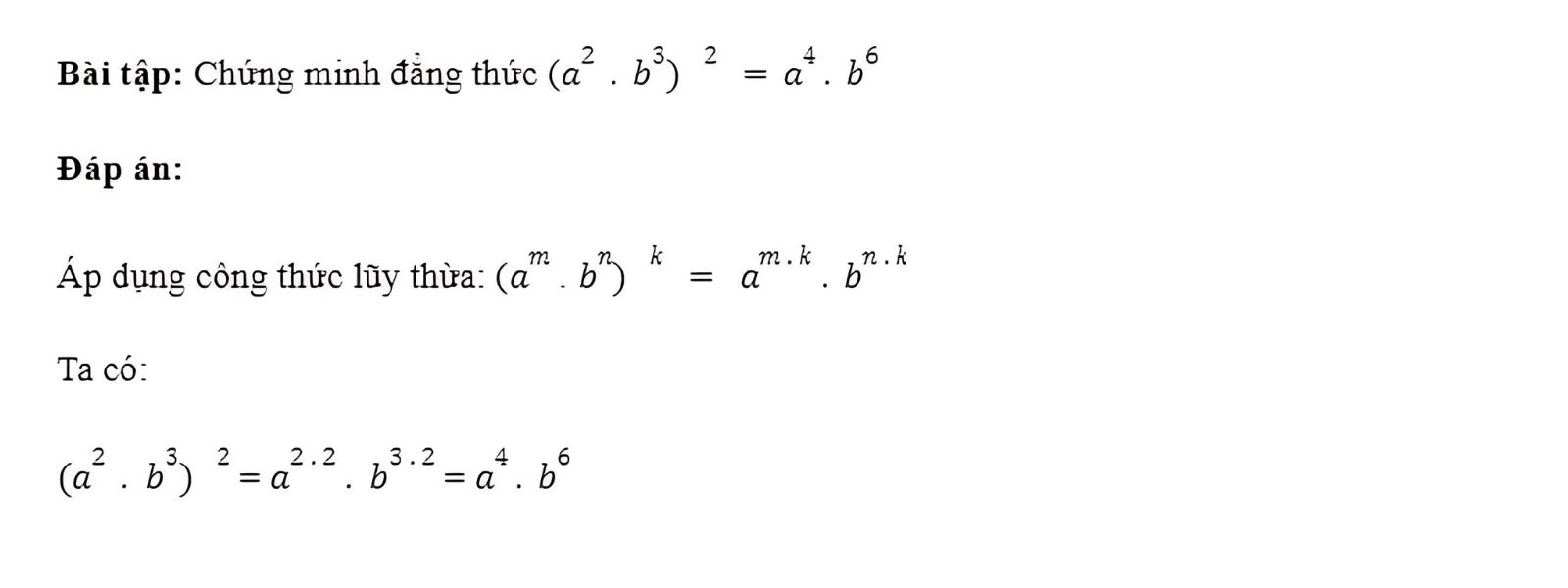
Lũy thừa là một kiến thức nền tảng trong toán học, đóng vai trò quan trọng trong việc giải quyết nhiều bài toán thực tế. Việc nắm vững các công thức và áp dụng thành thạo chúng sẽ giúp các em tự tin hơn trong quá trình học tập. Qua bài viết này, hy vọng các em học sinh đã có một cái nhìn tổng quan về các công thức lũy thừa và cách vận dụng hiệu quả.
Để việc học toán trở nên dễ dàng và thú vị hơn, ngoài cách học giỏi toán hiệu quả việc có một môi trường học tập hiện đại và đội ngũ giáo viên giàu kinh nghiệm là yếu tố không thể thiếu. Hiểu được điều này, Trường Việt Anh – một trong các trường tư thục uy tín tại TPHCM không ngừng nỗ lực tạo nên môi trường học tập lý tưởng cho các tài năng trẻ. Không chỉ sở hữu cơ sở vật chất hiện đại hàng đầu TP.HCM, đội ngũ giáo viên nhiều năm kinh nghiệm trong nghề, Trường Việt Anh còn đầu tư các chương trình đào tạo chuẩn quốc tế. Chúng tôi tự tin là nơi giúp các em trang bị kỹ năng và kiến thức toàn diện, sẵn sàng chinh phục mọi đỉnh cao tri thức.
Hãy liên hệ Trường Việt Anh ngay hôm nay để nhận tư vấn chi tiết:
- Hotline: 0916.961.409
- Website: https://truongvietanh.com/

