Cách xác định số điểm cực trị của hàm số chứa dấu giá trị tuyệt đối dựa trên công thức tính nhanh
Tuyển tập Đề thi thử Toán THPT Quốc gia 2020 có lời giải chi tiết
Trong khoá học PRO X các em đã được tiếp cận cách xác định số điểm cực trị của hàm trị tuyệt đối dựa trên cách suy đồ thị và bảng biến thiên. Ở bài viết này trình bày cho các em công thức tính nhanh:
Nội dung lý thuyết và ví dụ các bài toán trong bài viết này được trình bày tại khoá học vận dụng cao PRO XMAX
Nhận xét:
-
Số điểm cực trị của hàm số $left| f(x) right|$ bằng tổng số điểm cực trị của hàm số $f(x)$ và số nghiệm đơn và bội lẻ của phương trình $f(x)=0.$ Hay cách khác bằng tổngsố điểm cực trị của hàm số $f(x)$.
-
Số điểm cực trị của hàm số $fleft( left| x right| right)$ bằng $2a+1,$ trong đó $a$ là số điểm cực trị dương của hàm số $f(x).$
Đặc biệt với hàm số $f(x)=a{{x}^{3}}+b{{x}^{2}}+cx+d$ có hai điểm cực trị ${{x}_{1}},{{x}_{2}}.$ Khi đó hàm số $y=left| f(x) right|$ có $n$ điểm cực trị
-
$n=5Leftrightarrow {{f}_{cd}}.{{f}_{ct}}<0$ và tương đương với $f(x)=0$ có 3 nghiệm thực phân biệt
-
$n=3Leftrightarrow {{f}_{cd}}.{{f}_{ct}}ge 0.$
Ví dụ 1: Cho hàm số $fleft( x right)=m{{x}^{3}}-3m{{x}^{2}}+left( 3m-2 right)x-m.$ Số giá trị nguyên của tham số $min left[ -10;10 right]$ để hàm số $gleft( x right)=left| fleft( x right)+2 right|$ có $5$ điểm cực trị là
A. $10.$
B. $11.$
C. $9.$
D. $7.$
Giải. Ta có $mathbf{ycbt}Leftrightarrow fleft( x right)+2=0Leftrightarrow m{{x}^{3}}-3m{{x}^{2}}+left( 3m-2 right)x-m+2=0$
$Leftrightarrow left( x-1 right)left[ m{{left( x-1 right)}^{2}}-2 right]=0Leftrightarrow x=1vee m{{left( x-1 right)}^{2}}=2$ có 3 nghiệm phân biệt $Leftrightarrow m>0Rightarrow min left{ 1,…,10 right}.$ Chọn đáp án A.
Ví dụ 2: Cho hàm số $fleft( x right)=left( m-2 right){{x}^{3}}-2left( 2m-3 right){{x}^{2}}+left( 5m-3 right)x-2m-2.$ Số giá trị nguyên dương của tham số $m$ để hàm số $gleft( x right)=left| fleft( x right) right|$ có năm điểm cực trị là
A. $3.$
B. $2.$
C. $0.$
D. $1.$
Giải. Ta có $mathbf{ycbt}Leftrightarrow fleft( x right)=0Leftrightarrow left( m-2 right){{x}^{3}}-2left( 2m-3 right){{x}^{2}}+left( 5m-3 right)x-2m-2=0$
$Leftrightarrow left( x-2 right)left[ left( m-2 right){{x}^{2}}+left( 2-2m right)x+m+1 right]=0$
$ Leftrightarrow left[ begin{gathered} x = 2 hfill gleft( x right) = left( {m – 2} right){x^2} + left( {2 – 2m} right)x + m + 1 = 0 hfill end{gathered} right.$ có 3 nghiệm phân biệt
$ Leftrightarrow left{ begin{gathered} m – 2 ne 0 hfill gleft( 2 right) = 4left( {m – 2} right) + 2left( {2 – 2m} right) + m + 1 ne 0 hfill Delta ‘ = {left( {1 – m} right)^2} – left( {m – 2} right)left( {m + 1} right) > 0 hfill end{gathered} right. Leftrightarrow left{ begin{gathered} m ne 2 hfill m ne 3 hfill m < 3 hfill end{gathered} right. Leftrightarrow 2 ne m < 3 Rightarrow m = 1.$ Chọn đáp án D.
Ví dụ 3: Gọi $S$ là tập hợp tất cả các giá trị nguyên của tham số $m$ để hàm số $y=left| -{{x}^{3}}+3m{{x}^{2}}+3left( 1-{{m}^{2}} right)x+{{m}^{3}}-{{m}^{2}} right|$ có $5$ điểm cực trị. Tổng các phần tử của $S$ bằng
A. $-2.$
B. $3.$
C. $7.$
D. $4.$
Giải. Ta có $mathbf{ycbt}Leftrightarrow gleft( x right)=-{{x}^{3}}+3m{{x}^{2}}+3left( 1-{{m}^{2}} right)x+{{m}^{3}}-{{m}^{2}}=0$ có 3 nghiệm phân biệt (*)
Ta có ${g}’left( x right)=-3{{x}^{2}}+6mx+3left( 1-{{m}^{2}} right)=0Leftrightarrow x=m+1;x=m-1$
Vậy $left( * right)Leftrightarrow gleft( m+1 right)gleft( m-1 right)<0Leftrightarrow left( -{{m}^{2}}+3m+2 right)left( -{{m}^{2}}+3m-2 right)<0$
$ Leftrightarrow {left( { – {m^2} + 3m} right)^2} < 4 Leftrightarrow – 2 < – {m^2} + 3m < 2 Leftrightarrow left[ begin{gathered} 2 < m < dfrac{{3 + sqrt {17} }}{2} hfill dfrac{{3 – sqrt {17} }}{2} < m < 1 hfill end{gathered} right. Rightarrow m in left{ {0,3} right}.$ Chọn đáp án B.
Các bài toán biện luận số điểm cực trị của hàm tuyệt đối dạng |u(x)| ta đưa về xét dấu đồng thời của u(x) và u'(x). Chi tiết xem ví dụ:
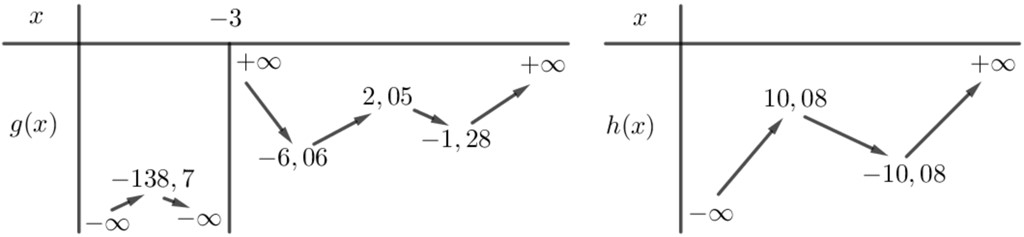
Ví dụ 1: Có bao nhiêu giá trị nguyên của tham số $m in left[ { – 200;200} right]$ để hàm số $fleft( x right)=left| {{x}^{4}}-7{{x}^{2}}-mleft( x+3 right)+6 right|$ có đúng $3$ điểm cực trị?
Giải. Xét [uleft( x right)={{x}^{4}}-7{{x}^{2}}-mleft( x+3 right)+6Rightarrow {u}’left( x right)=4{{x}^{3}}-14x-m]
[Rightarrow uleft( x right)=0Leftrightarrow m=gleft( x right)=dfrac{{{x}^{4}}-7{{x}^{2}}+6}{x+3};{u}’left( x right)=0Leftrightarrow m=hleft( x right)=4{{x}^{3}}-14x]
Ta có bảng biến thiên của $gleft( x right),hleft( x right)$ như sau:
Hàm số [fleft( x right)=left| uleft( x right) right|] có đúng 3 điểm cực trị khi và chỉ khi
TH1 : ${u}’left( x right)$ có 1 lần đổi dấu và $uleft( x right)$ có 2 lần đổi dấu $Rightarrow min left{ -200,…,-139,11,…,200 right}.$
TH2 : ${u}’left( x right)$ có 3 lần đổi dấu và $uleft( x right)$ có 0 lần đổi dấu $Rightarrow min left{ -10,…,-7 right}.$
Vậy $min left{ -200,…,-139,-10,…,-7,11,…,200 right}.$ Có tất cả $left( -139-left( -200 right)+1 right)+left( -7-left( -10 right)+1 right)+left( 200-11+1 right)=256$ giá trị nguyên của $min left[ -200;200 right]$ thoả mãn. Chọn đáp án D.
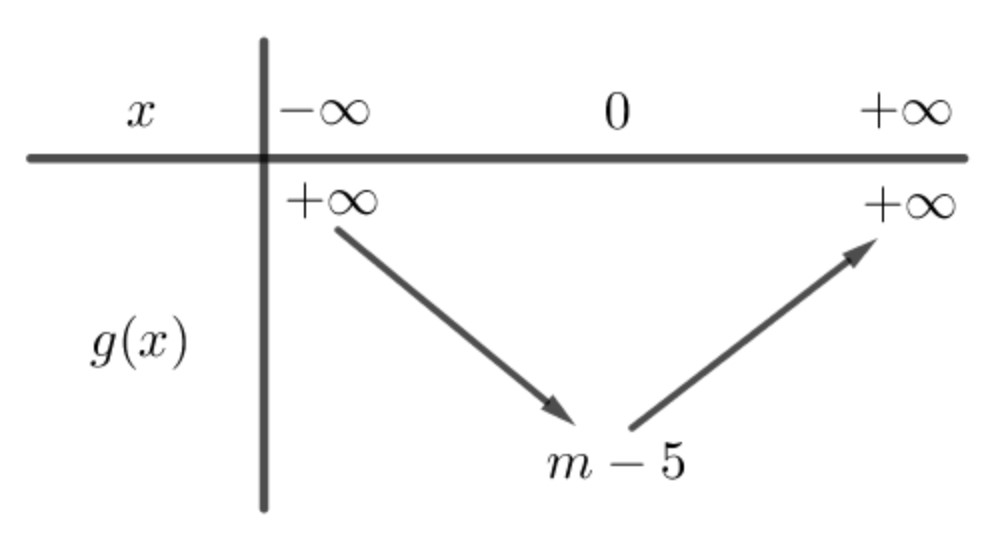
Ví dụ 2: Cho hàm số $fleft( x right)={{x}^{3}}-6{{x}^{2}}+9x-2.$ Có bao nhiêu giá trị nguyên dương của tham số $m$ để hàm số $y=left| fleft( {{x}^{2}}+m-5 right) right|$ có ít nhất 7 điểm cực trị?
A. $7.$
B. $6.$
C. $3.$
D. $8.$
Giải. Ta có $fleft( x right)=0Leftrightarrow x=2;x=2pm sqrt{3}$ và ${f}’left( x right)=3{{x}^{2}}-12x+9Rightarrow {f}’left( x right)=0Leftrightarrow x=1;x=3$
Xét $uleft( x right) = fleft( {{x^2} + m – 5} right) Rightarrow u’left( x right) = 2x.f’left( {{x^2} + m – 5} right) Rightarrow u’left( x right) = 0 Leftrightarrow left[ begin{gathered} x = 0 hfill {x^2} + m – 5 = 1 hfill {x^2} + m – 5 = 3 hfill end{gathered} right.$
Và $uleft( x right) = 0 Leftrightarrow left[ begin{gathered} {x^2} + m – 5 = 2 hfill {x^2} + m – 5 = 2 – sqrt 3 hfill {x^2} + m – 5 = 2 + sqrt 3 hfill end{gathered} right.$
Hàm số $gleft( x right)={{x}^{2}}+m-5$ có bảng biến thiên như sau:
Ta cần tìm điều kiện để tổng số lần đổi dấu của $uleft( x right)$ và ${u}’left( x right)$ ít nhất bằng 7.
Tức tổng số lần đổi dấu của $gleft( x right)-1;gleft( x right)-3;gleft( x right)-2;gleft( x right)-left( 2-sqrt{3} right);gleft( x right)-left( 2+sqrt{3} right)$ ít nhất bằng 6.
Vậy $m-5<2Leftrightarrow m<7Rightarrow min left{ 1,…,6 right}.$ Chọn đáp án B.
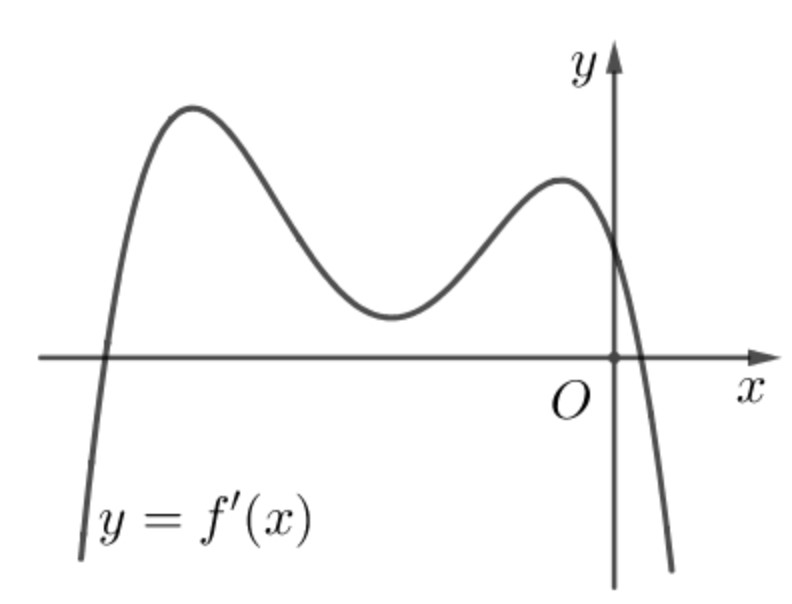
Ví dụ 2: Cho hàm số $f(x)$ có $f(0)=0$ và ${f}'(x)$ là đa thức bậc bốn có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số $g(x)=left| f({{x}^{3}})+x right|$ là
Xét $u=f({{x}^{3}})+x$ có ${u}’=0Leftrightarrow 3{{x}^{2}}{f}'({{x}^{3}})+1=0Leftrightarrow {f}'({{x}^{3}})=-dfrac{1}{3{{x}^{2}}}.$ Đặt $t={{x}^{3}}Leftrightarrow x=sqrt[3]{t},$ phương trình trở thành: [{f}'(t)=-dfrac{1}{3sqrt[3]{{{t}^{2}}}}(1).] Xét hàm số $y=-dfrac{1}{3sqrt[3]{{{x}^{2}}}}$ có ${y}’=dfrac{2}{9sqrt[3]{{{x}^{5}}}}.$ Bảng biến thiên:
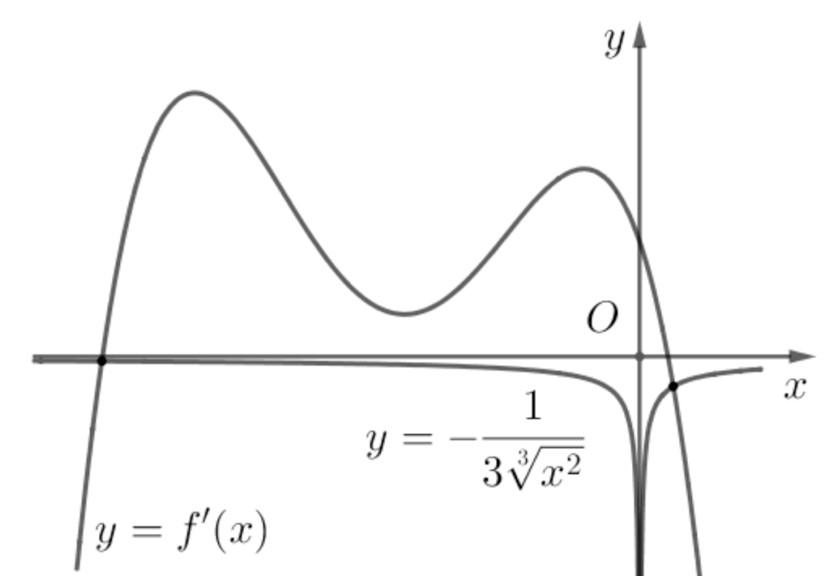
Suy ra đồ thị hàm số $y=-dfrac{1}{3sqrt[3]{{{x}^{2}}}}$ được vẽ cùng với đồ thị ${f}'(x)$ có dạng như hình vẽ bên:
Hai đường cong ${f}'(x)$ và $y=-dfrac{1}{3sqrt[3]{{{x}^{2}}}}$ cắt nhau tại hai điểm phân biệt có hoành độ $a<0<b.$ Vì vậy (1) có hai nghiệm là $t=a;t=b.$ Khi đó ${u}’=0$ có hai nghiệm $x=sqrt[3]{a};x=sqrt[3]{b}.$
Bảng biến thiên:
trong đó $u(0)=f(0)=0.$ Vì vậy hàm số $g(x)=left| u right|$ có tất cả $2+3=5$ điểm cực trị. Chọn đáp án B.
Ví dụ 3: Có bao nhiêu giá trị nguyên âm của tham số $a$ để hàm số $fleft( x right)=left| {{x}^{6}}+a{{x}^{3}}+48x right|$ có đúng $3$ điểm cực trị?
Giải. Xét $uleft( x right)={{x}^{6}}+a{{x}^{3}}+48xRightarrow {u}’left( x right)=6{{x}^{5}}+3a{{x}^{2}}+48$
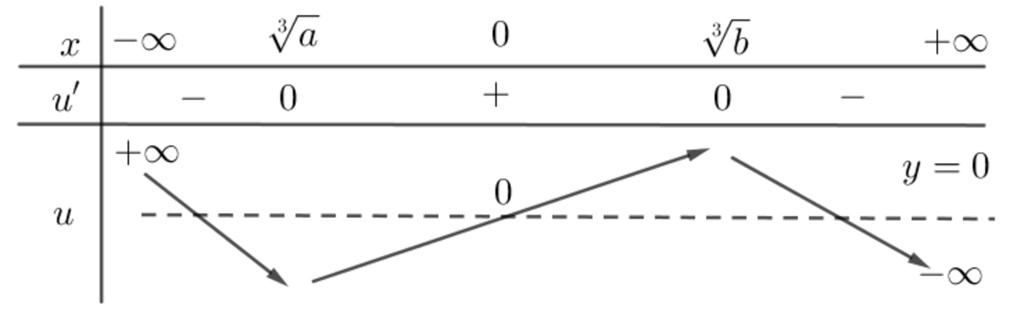
$ Rightarrow uleft( x right) = 0 Leftrightarrow left[ begin{gathered} x = 0 hfill a = gleft( x right) = – {x^3} – dfrac{{48}}{{{x^2}}} hfill end{gathered} right.;u’left( x right) = 0 Leftrightarrow a = hleft( x right) = – 2{x^3} – dfrac{{16}}{{{x^2}}}$Bảng biến thiên của hai hàm số $gleft( x right),hleft( x right)$ như sau:
Từ bảng biến thiên của $gleft( x right),hleft( x right)$ suy ra ${u}’left( x right)$có 3 lần đổi dấu hoặc 1 lần đổi dấu; $uleft( x right)$ có 4 lần đổi dấu hoặc 2 lần đổi dấu.
Vậy hàm số $fleft( x right)=left| uleft( x right) right|$ có đúng đúng 3 điểm cực trị khi và chỉ khi ${u}’left( x right)$ có 1 lần đổi dấu và $uleft( x right)$ có 2 lần đổi dấu suy ra $ain left{ -13,…,-1 right}.$ Chọn đáp án A.
Ví dụ 4: Có bao nhiêu giá trị nguyên của tham số $m$ để đồ thị hàm số $y=left| {{x}^{4}}-2m{{x}^{2}}-3 right|$ có đúng ba điểm cực trị $A,B,C$ và diện tích tam giác $ABC$ lớn hơn $1?$
Giải. Xét $uleft( x right)={{x}^{4}}-2m{{x}^{2}}-3.$ Ta có $uleft( 0 right)=-3<0.$
TH1: Nếu $uleft( x right)$ có 3 điểm cực trị $Leftrightarrow -2m<0$ thì $left| uleft( x right) right|$ có $5$ điểm cực trị (loại).
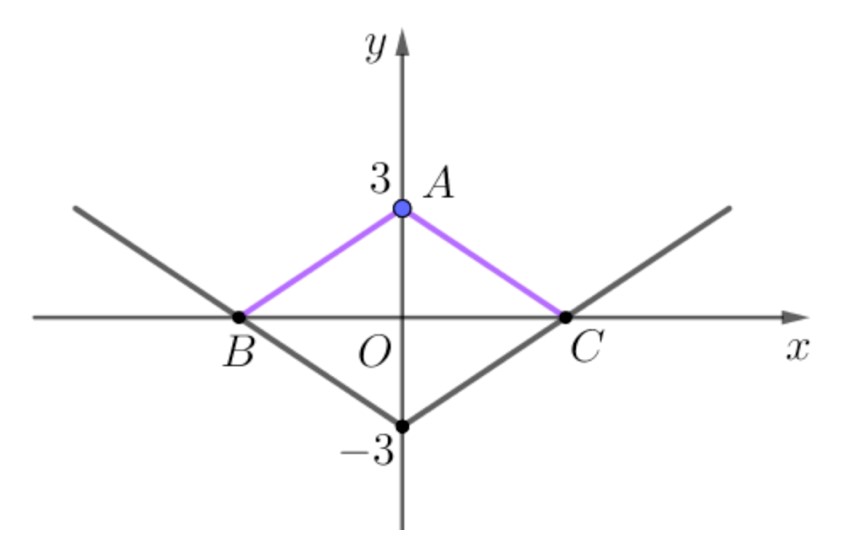
TH2: Nếu $uleft( x right)$ có đúng 1 điểm cực trị $Leftrightarrow -2mge 0$ thì $left| uleft( x right) right|$ có 3 điểm cực trị (thoả mãn).
Xét $uleft( x right)=0Leftrightarrow {{x}^{2}}=m+sqrt{{{m}^{2}}+3}Leftrightarrow x=pm sqrt{m+sqrt{{{m}^{2}}+3}}$
Khi đó toạ độ các điểm cực trị là $Aleft( 0;3 right),Bleft( -sqrt{m+sqrt{{{m}^{2}}+3}};0 right),Cleft( sqrt{m+sqrt{{{m}^{2}}+3}};0 right)$
$Rightarrow {{S}_{ABC}}=dfrac{1}{2}BC.AO=3sqrt{m+sqrt{{{m}^{2}}+3}}>1.$ Kết hợp với $mle 0$ nhận các giá trị nguyên $-13,…,0.$ Chọn đáp án A.
Ví dụ 5: Cho hàm số $fleft( x right)={{x}^{4}}-12{{x}^{3}}+30{{x}^{2}}+left( 4-m right)x,$ với $m$ là tham số thực. Có bao nhiêu giá trị nguyên của $m$ để hàm số $gleft( x right)=fleft( left| x right| right)$ có đúng $7$ điểm cực trị?
Giải. Số điểm cực trị của hàm số $gleft( x right)=fleft( left| x right| right)$ bằng $2a+1=7Leftrightarrow a=3,$ với $a$ là số điểm cực trị dương của hàm số $fleft( x right).$
Ta tìm điều kiện để hàm số $fleft( x right)$ có 3 điểm cực trị dương, tức là ${f}’left( x right)$ có 3 lần đổi dấu trên khoảng $left( 0;+infty right).$
Xét phương trình ${f}’left( x right)=0Leftrightarrow 4{{x}^{3}}-36{{x}^{2}}+60x+4-m=0Leftrightarrow m=4{{x}^{3}}-36{{x}^{2}}+60x+4=hleft( x right).$
Ta có $h’left( x right) = 12{x^2} – 72x + 60 Rightarrow h’left( x right) = 0 Leftrightarrow x = 1;x = 5.$
Bảng biến thiên:
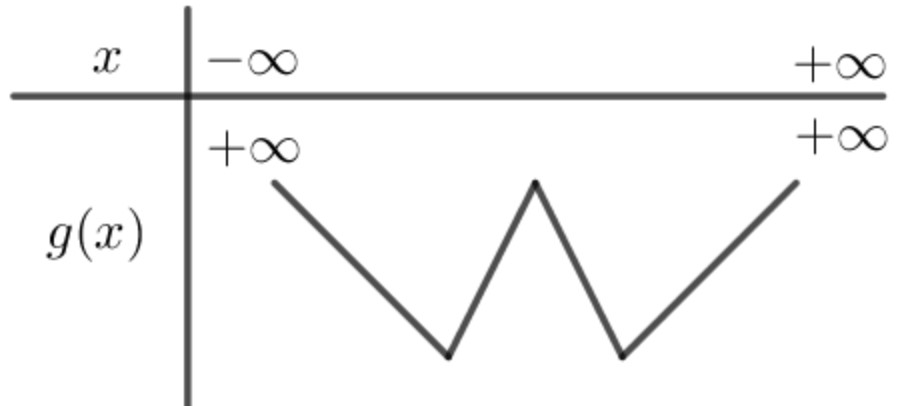
Vậy $4<m<32Rightarrow min left{ 5;6;…;31 right}$ có tất cả 27 số nguyên. Chọn đáp án A.
Ví dụ 6: Cho hàm số $f(x)=dfrac{1}{4}{{x}^{4}}-m{{x}^{3}}+dfrac{3}{2}({{m}^{2}}-1){{x}^{2}}+(1-{{m}^{2}})x+2019$ với $m$ là tham số thực. Biết rằng hàm số $y=fleft( left| x right| right)$ có số điểm cực trị lớn hơn 5 khi $a<{{m}^{2}}<b+2sqrt{c} (a,b,c in R).$ Giá trị $T=a+b+c$ bằng
Giải. Ta có ${f}'(x)={{x}^{3}}-3m{{x}^{2}}+3({{m}^{2}}-1)x+1-{{m}^{2}}$ là một đa thức bậc ba có tối đa 3 nghiệm, vì vậy hàm số $y=fleft( left| x right| right)$ có số điểm cực trị lớn hơn 5 khi và chỉ khi $f(x)$ có nhiều hơn 2 điểm cực trị dương tức là ${f}'(x)=0$ có 3 nghiệm dương phân biệt.
Ta có ${f}'(x)=0Leftrightarrow {{x}^{3}}-3m{{x}^{2}}+3({{m}^{2}}-1)x+1-{{m}^{2}}=0$ có 3 nghiệm dương phân biệt.
Xét hàm số $y={{x}^{3}}-3m{{x}^{2}}+3({{m}^{2}}-1)x+1-{{m}^{2}}$ có $y’ = 0 Leftrightarrow 3{x^2} – 6mx + 3({m^2} – 1) = 0 Leftrightarrow left[ begin{gathered} x = m – 1 hfill x = m + 1 hfill end{gathered} right. Rightarrow left{ begin{gathered} {x_{cd}} = m – 1 hfill {x_{ct}} = m + 1 hfill end{gathered} right. Rightarrow left{ begin{gathered} {y_{cd}} = {m^3} – {m^2} – 3m + 3 hfill {y_{ct}} = {m^3} – {m^2} – 3m – 1 hfill end{gathered} right..$
Do đó phương trình $y=0$ có 3 nghiệm dương phân biệt khi và chỉ khi
$ Leftrightarrow left{ begin{gathered} {x_{cd}} > 0 hfill y(0) < 0 hfill {y_{cd}}.{y_{ct}} < 0 hfill end{gathered} right. Leftrightarrow left{ begin{gathered} m – 1 > 0, hfill 1 – {m^2} < 0, hfill ({m^3} – {m^2} – 3m + 3)({m^3} – {m^2} – 3m – 1) < 0 hfill end{gathered} right. Leftrightarrow sqrt 3 < m < 1 + sqrt 2 Rightarrow 3 < {m^2} < 3 + 2sqrt 2 .$
Vì vậy $a=3,b=3,c=2Rightarrow a+b+c=3+3+2=8.$ Chọn đáp án B.
Ví dụ 7: Cho hàm số $fleft( x right)=dfrac{2}{5}{{x}^{5}}-dfrac{m}{2}{{x}^{4}}+dfrac{4left( m+3 right)}{3}{{x}^{3}}-left( m+7 right){{x}^{2}},left( min mathbb{R} right).$ Có bao nhiêu số nguyên $m$ để hàm số $gleft( x right)=fleft( left| x right| right)$ có đúng 1 điểm cực đại?
Giải. Ta có $underset{xto infty }{mathop{lim }},gleft( x right)=+infty Rightarrow gleft( x right)$ có đúng 1 điểm cực đại$Leftrightarrow gleft( x right)$ có đúng 3 điểm cực trị$Leftrightarrow fleft( x right)$ có đúng 1 điểm cực trị dương
$Leftrightarrow {f}’left( x right)=2{{x}^{4}}-2m{{x}^{3}}+4left( m+3 right){{x}^{2}}-2left( m+7 right)x=2xleft( {{x}^{3}}-m{{x}^{2}}+2left( m+3 right)x-m-7 right)$
$=2xleft( x-1 right)left( underbrace{{{x}^{2}}+left( 1-m right)x+m+7}_{hleft( x right)} right)$ đổi dấu đúng 1 lần trên khoảng $left( 0;+infty right)$
$Leftrightarrow hleft( x right)$ không đổi dấu trên khoảng $left( 0;+infty right)$ và vì $underset{xto +infty }{mathop{lim }},hleft( x right)=+infty $ nên điều kiện sẽ là
$Leftrightarrow hleft( x right)={{x}^{2}}+left( 1-m right)x+m+7ge 0,forall xin left[ 0;+infty right)$
$Leftrightarrow mleft( 1-x right)ge -{{x}^{2}}-x-7,forall xin left[ 0;+infty right);gleft( x right)=dfrac{-{{x}^{2}}-x-7}{1-x}$
$Leftrightarrow left{ begin{gathered}hfill mge gleft( x right),forall xin left[ 0;1 right) hfill mle gleft( x right),forall xin left( 1;+infty right) end{gathered} right.Leftrightarrow left{ begin{gathered}hfill mge underset{left[ 0;1 right)}{mathop{max }},gleft( x right)=gleft( 0 right)=-7 hfill mle underset{left( 1;+infty right)}{mathop{min }},gleft( x right)=gleft( 4 right)=9 end{gathered} right.$
Vậy $min left{ -7,…,9 right}.$
Chọn đáp án A.
Cách 2: TH1: ${{Delta }_{h}}le 0Leftrightarrow {{left( 1-m right)}^{2}}-4left( m+7 right)le 0Leftrightarrow -3le mle 9$
TH2: ${{Delta }_{h}}>0Leftrightarrow m<-3vee m>9$ điều kiện là $hleft( x right)$ có hai nghiệm ${{x}_{1}}<{{x}_{2}}le 0Leftrightarrow left{ begin{gathered}hfill {{Delta }_{h}}>0 hfill S<0 hfill Pge 0 end{gathered} right.Leftrightarrow left{ begin{gathered}hfill m<-3vee m>9 hfill m-1<0 hfill m+7ge 0 end{gathered} right.Leftrightarrow -7le m<-3.$
Vậy $min left{ -7,…,9 right}.$ Chọn đáp án A.
Ví dụ 8: Cho hàm số bậc ba $y=fleft( x right).$ Biết $fleft( -2 right)=0$ và ${f}’left( x right)$ có bảng xét dấu như sau: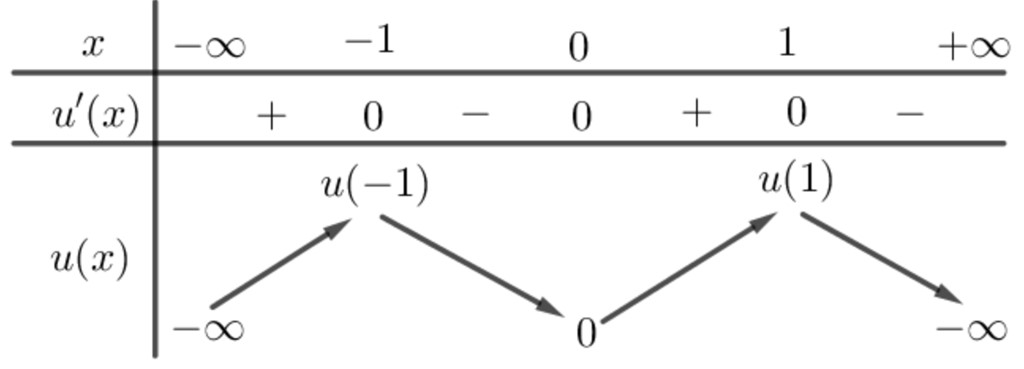
Hàm số $gleft( x right)=left| 15fleft( -{{x}^{4}}+2{{x}^{2}}-2 right)-10{{x}^{6}}+30{{x}^{2}} right|$ có bao nhiêu điểm cực trị?
Giải. Xét $uleft( x right)=15fleft( -{{x}^{4}}+2{{x}^{2}}-2 right)-10{{x}^{6}}+30{{x}^{2}};uleft( 0 right)=15fleft( -2 right)=0$
Và ${u}’left( x right)=15left( -4{{x}^{3}}+4x right){f}’left( -{{x}^{4}}+2{{x}^{2}}-2 right)-60{{x}^{5}}+60x$
$=60xleft( -{{x}^{2}}+1 right)left[ {f}’left( -{{x}^{4}}+2{{x}^{2}}-2 right)+1+{{x}^{2}} right]=60xleft( -{{x}^{2}}+1 right)left[ {f}’left( -{{left( {{x}^{2}}-1 right)}^{2}}-1 right)+1+{{x}^{2}} right]$
Vì $-{{left( {{x}^{2}}-1 right)}^{2}}-1le -1,forall xRightarrow {f}’left( -{{left( {{x}^{2}}-1 right)}^{2}}-1 right)ge 0Rightarrow {f}’left( -{{left( {{x}^{2}}-1 right)}^{2}}-1 right)+1+{{x}^{2}}>0$
Do đó ${u}’left( x right)=0Leftrightarrow xleft( -{{x}^{2}}+1 right)=0Leftrightarrow x=0;x=pm 1.$
Bảng biến thiên:Suy ra $uleft( x right)$ có 2 lần đổi dấu và có 3 điểm cực trị nên $gleft( x right)=left| uleft( x right) right|$ có tất cả 5 điểm cực trị. Chọn đáp án B.
Các em xem lại Bài giảng Số điểm cực trị hàm trị tuyệt đối khoá VDC XMAX.
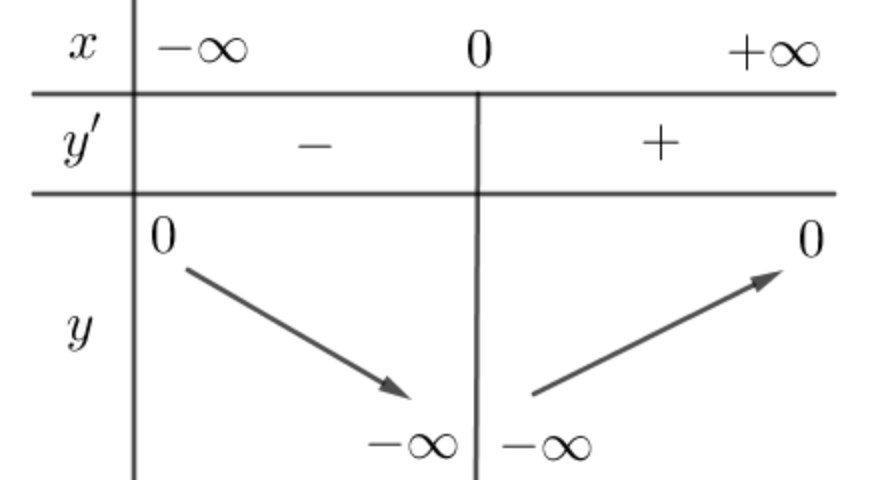
Ví dụ 9: Cho hàm số bậc ba $y=fleft( x right)$có đồ thị của hàm đạo hàm ${f}’left( x right)$ như hình vẽ và $fleft( b right)=1$.
Số giá trị nguyên của $min left[ -5;5 right]$ để hàm số $gleft( x right)=left| {{f}^{2}}left( x right)+4fleft( x right)+m right|$ có đúng 5 điểm cực trị là
A. $8$.
B. $10$.
C. $9$.
D. $7$.
Giải. Ta có bảng biến thiên của hàm số $y=fleft( x right)$:
Xét hàm số $hleft( x right)={{f}^{2}}left( x right)+4fleft( x right)+m$.
Ta có ${h}’left( x right)=2{f}’left( x right)fleft( x right)+4{f}’left( x right)=2{f}’left( x right)left[ fleft( x right)+2 right]$.
Khi đó ${h}’left( x right)=0Rightarrow 2{f}’left( x right)left[ fleft( x right)+2 right]=0Leftrightarrow left[ begin{gathered}hfill {f}’left( x right)=0 hfill fleft( x right)=-2 end{gathered} right.Leftrightarrow left[ begin{gathered}hfill x=a;,x=b hfill x=c,,left( c,,langle ,,a right) end{gathered} right.$.
Vậy ${h}’left( x right)=0$ có $3$ nghiệm phân biệt $Rightarrow $$hleft( x right)$có $3$ điểm cực trị.
Xét $hleft( x right)=0$$Leftrightarrow {{f}^{2}}left( x right)+4fleft( x right)=-m,,left( * right)$.
Để $gleft( x right)=left| hleft( x right) right|$có $5$ điểm cực trị khi và chỉ khi PT $left( * right)$có $2$ nghiệm đơn hoặc nghiệm bội lẻ phân biệt.
Xét hàm số $tleft( x right)={{f}^{2}}left( x right)+4fleft( x right)$.
Ta có ${t}’left( x right)=2.fleft( x right).{f}’left( x right)+4{f}’left( x right)=2{f}’left( x right)left[ fleft( x right)+2 right]$.
Khi đó ${t}’left( x right)=0Leftrightarrow 2{f}’left( x right)left[ fleft( x right)+2 right]=0Leftrightarrow left[ begin{gathered}hfill {f}’left( x right)=0 hfill fleft( x right)=-2 end{gathered} right.$$Leftrightarrow left[ begin{gathered}hfill x=a;,x=b hfill x=c,,left( c,,langle ,,a right) end{gathered} right.$.
Ta có $tleft( c right)={{f}^{2}}left( c right)+4fleft( c right)={{left( -2 right)}^{2}}-8=-4.$ $tleft( b right)={{f}^{2}}left( b right)+4fleft( b right)=5.$
Ta có bảng biến thiên của $tleft( x right)$:
Từ YCBT $Leftrightarrow tleft( x right)=-m$ có hai nghiệm đơn hoặc nghiệm bội lẻ phân biệt
$Leftrightarrow left{ begin{gathered}hfill left[ begin{gathered}hfill -mge tleft( a right)>5 hfill -4<-mle 5 end{gathered} right. hfill -5le mle 5;,min mathbb{Z} end{gathered} right.Leftrightarrow left{ begin{gathered}hfill left[ begin{gathered}hfill mle -tleft( a right)<-5 hfill -4<-mle 5 end{gathered} right. hfill -5le mle 5, end{gathered} right.Leftrightarrow left{ begin{gathered}hfill -5le m<4 hfill min mathbb{Z} end{gathered} right.$
$Leftrightarrow min left{ -5;-4;-3;-2;-1;0;1;2;3 right}.$ Vậy có $9$ giá trị nguyên của $m$ thỏa mãn yêu cầu bài toán. Chọn đáp án C.
Bài tập tự luyện:
(a) Có bao nhiêu giá trị nguyên của tham số $a$ để hàm số $fleft( x right)=left| {{x}^{3}}+2{{x}^{2}}-ax-1 right|$ có đúng $3$ điểm cực trị?
(b) Có bao nhiêu giá trị nguyên của tham số $a$ để hàm số $y=left| {{x}^{4}}+a{{x}^{2}}-64x right|$ có đúng $5$ điểm cực trị?
>>Xem thêm Cập nhật Đề thi thử tốt nghiệp THPT 2023 môn Toán có lời giải chi tiết
