Một trong những chuyên đề quan trọng của Giải tích Toán 12 là nguyên hàm và nó thường xuất hiện nhiều trong các kì thi cuối kỳ ở trường và cả kỳ thi trung học phổ thông quốc gia. Vậy nên, các bạn rất nên chú ý học phần này nhé. Nhưng có những công thức nguyên hàm quan trọng nào cần nhớ?
Tài Liệu Học Tập sẽ giúp các bạn tổng hợp tất tần tật các công thức nguyên hàm đầy đủ từ cơ bản đến nâng cao và giới thiệu 2 phương pháp giải bài tập nguyên hàm thường gặp qua bài viết dưới đây.
Xem thêm: Tổng hợp công thức toán 12 ôn thi đại học.
1. Vậy nguyên hàm là gì?
Trước khi, đi sâu vào tìm hiểu công thức về nguyên hàm, các em cần nắm vững khái niệm nguyên hàm cũng như các tính chất và định lý liên quan.
1.1 Định nghĩa nguyên hàm
Cho hàm số f(x) xác định trên K, lúc này hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F’(x) = f(x) (với mọi x ∊ K, K có thể là khoảng, đoạn hoặc nửa đoạn trên ℝ).
Kí hiệu nguyên hàm của hàm số f(x) là:

1.2 Định lý nguyên hàm
3 định lý của nguyên hàm là:
- Định lý 1: Giả sử F(x) là một nguyên hàm của f(x) trên K. Khi đó, với mỗi hằng số C, hàm số G(x) = F(x) + C cũng là một nguyên hàm của f(x).
- Định lý 2: Trên K, nếu F(x) là một nguyên hàm của hàm số f(x) thì mọi nguyên hàm của f(x) trên K đều có dạng F(x) + C, với C là một hằng số tùy ý.
- Định lý 3: Trên K, tất cả hàm số f(x) liên tục đều có nguyên hàm.
1.3 Tính chất nguyên hàm
3 tính chất cơ bản của nguyên hàm được thể hiện như sau:

2. Ba bảng công thức nguyên hàm quan trọng (cơ bản, mở rộng, nâng cao)
Mỗi dạng nguyên hàm đều có những công thức riêng. Những công thức này đã được tổng hợp thành các bảng dưới đây để các em dễ dàng phân loại, ghi nhớ và áp dụng chính xác.
2.1 Bảng công thức nguyên hàm cơ bản

2.2 Bảng công thức nguyên hàm mở rộng

2.3 Bảng công thức nguyên hàm nâng cao

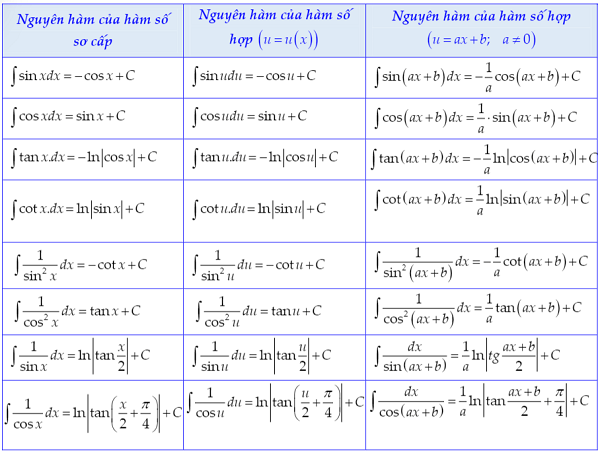
2.4 Bảng nguyên hàm hàm số lượng giác
3. Hai phương pháp giải bài tập nguyên hàm phổ biến
3.1 Phương pháp đổi biến số
Biến đổi số là phương pháp được áp dụng khá nhiều khi giải bài tập nguyên hàm. Vậy nên các bạn hãy chú ý nắm vững phương pháp giải này để làm bài tập nguyên hàm nhanh nhất.
Phương pháp đổi biến loại 1:
Cho hàm số u = u(x) có đạo hàm liên tục trên K, y = f(u) liên tục để f[u(x)] xác định trên K và ∫f(u)du = F(u) + C thì: ∫f[u(x)]u'(x)dx = F[u(x)] + C
Hướng dẫn giải:
Trước tiên, chọn t = φ(x) và tính vi phân hai vế: dt = φ'(t)dt.
Tiếp theo, biến đổi biểu thức thành: f(x)dx = f[φ(t)]φ'(t)dt = g(t)dt.
Kết quả: I = ∫f(x)dx = ∫g(t)dt = G(t) + C.
Phương pháp đổi biến loại 2: Khi đề bài cho hàm số f(x) liên tục trên K và x = φ(t) là một hàm số xác định, liên tục trên K và có đạo hàm là φ'(t). Lúc này:
∫f(x)dx = ∫f[φ(t)].φ'(t)dt
Hướng dẫn giải:
Trước hết, chọn x = φ(t) và lấy vi phân hai vế: dx = φ'(t)dt.
Thực hiện biến đổi: f(x)dx = f[φ(t)]φ'(t)dt = g(t)dt.
Tính: ∫f(x)dx = ∫g(t)dt = G(t) + C.
3.2 Phương pháp nguyên hàm từng phần
Phương pháp nguyên hàm từng phần chung:

Các dạng nguyên hàm từng phần thường gặp
Dạng nguyên hàm từng phần thường gặp 1:
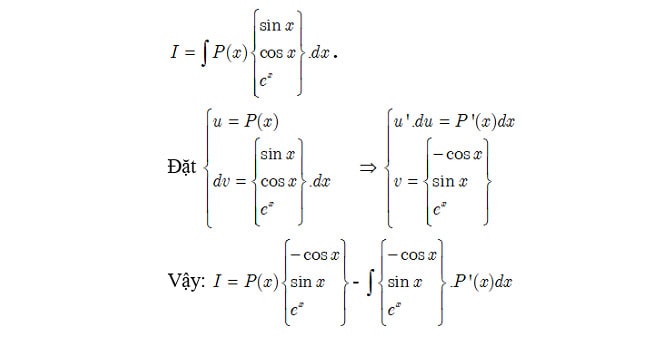
Dạng nguyên hàm từng phần thường gặp 2:
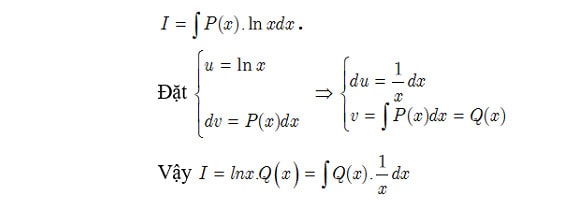
Dạng nguyên hàm từng phần thường gặp 3:

Như vậy, bài viết đã cung cấp đầy đủ các công thức nguyên hàm đầy đủ từ cơ bản, mở rộng đến nâng cao cho các bạn. Mong rằng tài liệu này sẽ giúp các bạn ôn tập hiệu quả cho các kì kiểm tra và kì thi môn toán, đặc biệt là cho kỳ thi THPT quốc gia sắp tới. Chúc cho tất cả các bạn đọc được bài viết này đều đạt được kết quả mình mong muốn!
Tham gia group Tài Liệu Học Tập để lấy đề thi các bạn nhé !
Xem thêm: Đề thi toán thpt quốc gia 2022.














Discussion about this post