Cấp số nhân là gì? Công thức cấp số nhân như thế nào? Cần phải nhớ những công thức quan trọng hay tính chất gì về dạng toán quan trọng này trong chương trình toán lớp 11 ? Trong bài viết dưới đây, Tài Liệu Học Tập sẽ giúp các bạn tổng hợp tất tần tật những kiến thức trọng tâm nhất về công thức cấp số nhân lớp 11 . Cùng với đó là 6 bài tập liên quan đến phần này.
1. Cấp số nhân là gì? Công thức cấp số nhân cần biết.
Trong những năm gần đây bài toán sử dụng công thức cấp số nhân, cấp số cộng vẫn thường được đưa vào trong đề thi tốt nghiệp trung học phổ thông quốc gia. Ngoài ra nó chắc chắn xuất hiện trong đề thi cuối học kì 1 lớp 11 môn toán. Dù dạng này khá đơn giản nhưng không phải ai cũng có thể làm thành thạo và chính xác. Nếu bỏ hoặc làm sai câu dễ như này thì thật tiếc phải không. Để giúp bạn lấy trọng điểm phần này, bài viết sẽ nêu rõ định nghĩa, công thức cần học.

Lý thuyết chung
- Công thức tổng quát: un+1=un.q
- Số hạng bất kì: un=u1.qn–1
- Tổng n số hạng đầu tiên: Sn=u1+u2+…+un=u11–qn1–q
2. Bài tập cấp số nhân có lời giải chi tiết
Sau khi biết công thức cấp số nhân thì việc làm bài tập là không thể thiếu nếu muốn được điểm cao. Dưới đây là 6 bài tập quan trọng có kèm lời giải chi tiết. Cùng tham khảo nhé!
Bài tập 1. Cho cấp số nhân ( un ), biết công bội q = 4 và số hạng đầu tiên u1 = 5. Hãy tìm số hạng thứ 2
A. 25
B. 20
C. 30
D. 40
Cách giải:
Áp dụng công thức cấp số nhân: u(n+1)=un.q
- q = 4
- Số hạng thứ 2: n + 1 = 2 => n = 1
- u1 = 5
Thay số vào: u(1+1)=u1.q ⇒ u2 = 5.4 = 20
Chọn đáp án B.
Bài tập 2. Cho cấp số nhân ( un ), biết số hạng đầu tiên u1 = 9 và số hạng kế tiếp u2 = 18. Hãy tìm công bội của dãy số này
A. 2
B. 3
C. 4
D. 5
Cách giải:
Áp dụng công thức tổng quát: u(n+1) = un.q
- u1 = 9
- u2 = 18
Thay số vào công thức ta có: u2=u1.q ⇒ 18=9.q ⇒ q = 18/9 =2
Chọn đáp án A.
Bài tập 3. Cho cấp số nhân ( un ), biết rằng số hạng đầu tiên u1 = 6, công bội là 2. Hãy tìm số hạng thứ 4.
A. 95
B. 48
C. 49
D. 36
Cách giải:
Áp dụng công thức số hạng bất kì ta có:
![]()
- u1 = 6
- q = 2
- n = 4
Thay số vào: u5= 6. 8 = 48
Chọn đáp án B.
Bài tập 4. Cho cấp số nhân (un), biết công bội q = – 3 và số hạng đầu tiên u1 = 4. Hãy tỉnh tổng của 6 số hạng đầu tiên
A. 730
B. 80
C. 120
D. 70
Cách giải:
Áp dụng công thức tính tổng của n số hạng đầu tiên:
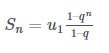
- q = – 3
- u1 = 4
Thay số vào ta được: S6 = 730
Chọn đáp án A.
Bài tập 5. Cho cấp số nhân (un), biết rằng u1 = – 0,5 và số hạng thứ 7 là u7 = – 32. Hãy tìm công bội
A. q = 4
B. q = ±1
C. q = ± 2
D. q = ± 3
Cách giải:
Áp dụng công thức số hạng bất kì:
![]()
- n = 7
- u1 = – 0,5
- u7 = – 32
Thay số vào: –32 = (–0,5).q^6
⇒ q=±2
Chọn đáp án C.
Bài tập 6. Biết rằng một cấp số nhân (un) có số hạng đầu u1 = 6, công bội q = 3 và số hạng thứ n là un = 486. Hỏi n bằng bao nhiêu
A. 4
B. 5
C. 6
D. 7
Cách giải:
Áp dụng công thức ta có:
![]()
- u1 = 6
- q = 3
- un = 486
Thay số vào: 486 = 6.3^(n–1)
⇒ 3^(n–1)=81 ⇒ 3^(n-1) = 3^4
=> n – 1 = 4=> n = 5
Chọn đáp án B.
Xem thêm: Công thức đạo hàm lớp 11
Vậy là bài viết đã tổng hợp toàn bộ kiến thức về công thức cấp số nhân và kèm theo 6 bài tập minh họa siêu chi tiết, cụ thể cho các bạn rồi. Hy vọng bài viết sẽ có ích cho bạn trong quá trình học môn toán. Nếu có bất kì thắc mắc hay khó hiểu đừng ngại comment xuống dưới nhé. Tài Liệu Học Tập sẽ cố gắng giải đáp bạn nhanh nhất có thể.
Tham gia group Tài Liệu Học Tập để lấy đề thi các bạn nhé !




Discussion about this post